2. Методы построения точечных оценок

Метод моментов для нахождения точечных оценок неизвестных параметров распределения наблюдаемой в выборке случайной величины , состоит в приравнивании теоретических моментов к выборочным моментам. Для нахождения параметров начальные или центральные моменты до порядка включительно приравниваются к соответствующим эмпирическим выборочным моментам , тем самым получим систему нелинейных уравнений метода моментов.

или .

Например, построим оценку параметра, а случайной величины , имеющей треугольное распределение (рис.12.1), по заданной выборке , где n – объем выборки:

f(x)

+1

-1 0 a +1

Рис. 12.1. Треугольное распределение

Поскольку неизвестный параметр один то, вычисляя и приравнивая только первые начальные теоретические и эмпирические моменты

, ,

получим оценку .

Метод моментов прост в применении и дает состоятельные оценки, однако их эффективность и несмещенность требуют дополнительных исследований.

Метод максимального правдоподобия основан на принципе правдоподобия, состоящем в том, что наблюдаемые в опыте события имеют большую вероятность, а маловероятные события практически не наблюдаемы. Вероятность наблюдения в опыте выборки оценивается функцией правдоподобия

… ,

поскольку данная нам выборка уже получена в опыте, то она должна обладать максимальным правдоподобием. За оценку неизвестного параметра распределения принимается его значение, при котором функция правдоподобия максимальна, поэтому уравнение метода для нахождения оценки :

, при условии .

Для решения этих уравнений чаще используется логарифм функции правдоподобия , поскольку максимум этих функций достигается при одном значении неизвестного параметра .

Например, рассмотрим случайную величину Пуассона с плотностью распределения , где неизвестный параметр распределения. Тогда функция правдоподобия и уравнение метода имеют вид:

….

.

Доказано что метод максимального правдоподобия позволяет строить состоятельные и эффективные оценки.

Метод наименьших квадратов основан на идее минимизации суммы квадратов отклонения выборочных данных (или их функции) от определяемой оценки, он не требует знания закона распределения наблюдаемой случайной величины и кратко называется методом МНК.

Например, рассмотрим оценку дисперсии случайной величины по выборке , где n – объем выборки. Построим функцию для квадратов отклонения ,

из условия минимума и находим

.

3. Интервальные оценки и алгоритм их построения

В отличие от точечных оценок типа интервальные оценки задают интервал значений, где оцениваемый параметр находится с заданной вероятностью, т.е. это оценки типа .

Надежностью оценки (доверительной вероятностью) называется вероятность , с которой оцениваемый параметр находится в интервале:

.

Полуширина доверительного интервала называется точностью оценки, соответствующей надежности . Для построения доверительного интервала (нахождения по величины ) необходимо знать закон распределения оценки случайной величины .

Пусть в выборке наблюдается нормальная случайная величина c неизвестными параметрами распределения а и .

Построим доверительный интервал для математического ожидания а:

,

принимая за точечную оценку а, величину и учитывая что величина имеет распределение Стьюдента с степенью свободы. Решение уравнения относительно при заданном значении эквивалентно решению уравнения:

или .

Его решение получим в виде , где двухсторонняя квантиль Стьюдента (рис. 12.2).

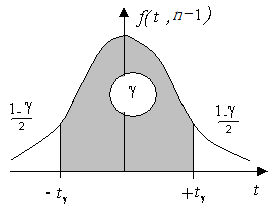
Рис. 12.2 Двухсторонняя квантиль Стьюдента

Построим теперь доверительный интервал для среднеквадратического отклонения :

.

Принимая за оценку величину и учитывая, что величина имеет -распределение с n - 1 степенью свободы. Решение уравнение относительно при заданном параметре эквивалентно решению уравнения:

,

тогда получим его решение в виде , где величины являются правосторонними “хи-квадрат” квантилями (рис.12.3).

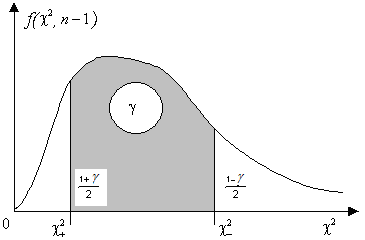
Рис. 12.3 Двухсторонняя “хи-квадрат”квантиль.

Пример: Пусть наблюдается выборка объемом n =16 со средним выборочным значением и выборочной дисперсией . Построить доверительные интервалы для неизвестного математического ожидания а и среднеквадратического отклонения для надежности .

Исправленная дисперсия , а исправленное выборочное среднеквадратическое отклонение .

По таблице квантилей для распределения Стьюдента в приложении 3 находим , тогда и доверительный интервал для математического ожидания а будет

20,2-0,43< a <20,2+0,43 или 19,77< a <20,63.

По таблице для квантилей - распределения в приложении 4 находим и тогда .

82