3. Выборочные характеристики

Помимо полигона и гистограммы выборка характеризуется следующими числовыми величинами:

Основные характеристики

~ выборочное среднее;

~ выборочная дисперсия;

~ выборочное среднеквадратическое отклонение;

~ исправленная выборочная дисперсия;

~ исправленное выборочное среднеквадратическое

отклонение (выборочный стандарт).

Дополнительные характеристики

~ выборочный начальный момент порядка k;

~ выборочный центральный момент порядка k;

Часто используются моменты 3-го и 4-го порядков в следующей форме:

~ выборочная асимметрия;

~ выборочный эксцесс.

В статистической практике рассматриваются так же групповые характеристики, например, в интервальных группах гистограммы выборки вычисляются средние интервальные значения и дисперсии.

Пример 3. Рассмотрим вычисление выборочных характеристик для выборки, представленной в примере 1. У этой выборки объема имеется m=13 вариант и столько же соответствующих им частот , которые расположены в первых двух столбцах табл. 4.

Таблица 4

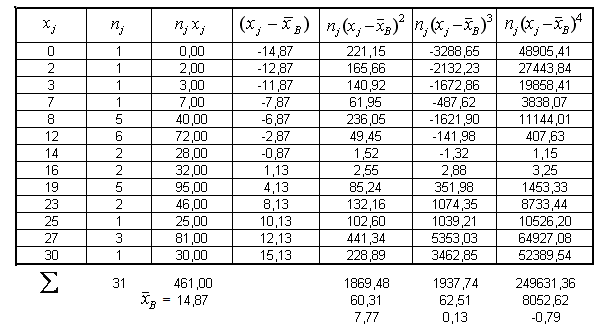
В последующих столбцах табл. 4, в соответствие с методом сводных таблиц, приводится расчет выборочных моментов и выборочных характеристик через варианты и частоты выборки:

; ; ;

;

Причем выполняется .

; ;

; .

Отметим, что все приведенные числовые характеристики являются случайными величинами, поскольку получены по элементам случайно взятой выборки. На элементах другой выборки наблюдений над той же случайной величиной числовые характеристики в общем случае изменят свое значение, то есть характеристики являются функцией от выборки , например:

; .

Лекция № 11

Выборочные распределения

Если наблюдаемая случайная величина является нормальной, т.е , где - математическое ожидание, - среднеквадратическое отклонение, то случайная величина среднего выборочного так же является нормальной . Здесь нормальные случайные величины, совпадающие с наблюдаемой величиной. Рассмотрим стандартные нормальные величины в виде:

,

и построим из них случайные величины Пирсона и Стьюдента .

Тогда получим [9,10]:

,

.

Отсюда видно, что случайная величина выборочной дисперсии D_В распределена пропорционально «Хи-квадрат» случайной величине с n степенями свободы, а отклонение выборочного среднего от математического ожидания распределено пропорционально t-величине Стьюдента с n-1 степенью свободы.

При сравнении двух выборок объемов n₁ и n₂ часто используется случайная величина Фишера со степенями свободы n₁ и n₂ :

.

1. Распределения Стьюдента и Пирсона

Распределения величин и известны аналитически в виде функции плотности распределения вероятностей

з десь - функция Эйлера, обладающая свойством , в силу которого при целом положительном имеет место

Графический вид функций плотности представлен ниже на рис. 11.1, 11.2 для различного количества степеней свободы.

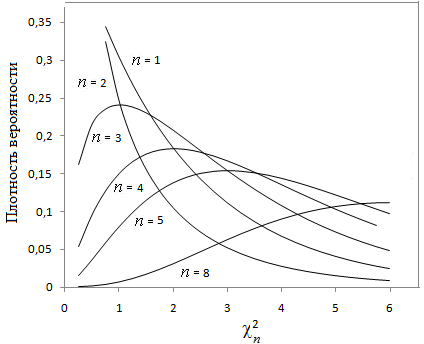
Рис.11.1 Кривые «Хи-квадрат» распределения

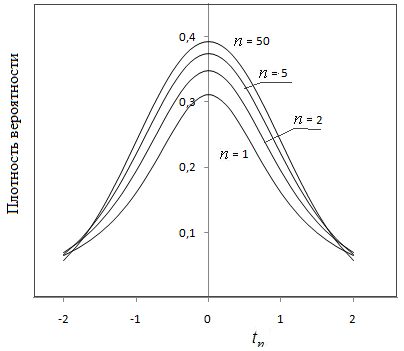
Рис.11.2 Кривые распределения Стьюдента

Числовые характеристики распределений «Хи-квадрат» и Стьюдента следующие:

, , , .

Можно заметить, что с ростом числа степеней свободы, указанные распределения будут приближаться к нормальному распределению, что соответствует центральной предельной теореме теории вероятностей.