Математичечская статистика

Лекция № 10

Выборочный метод

Для установления закономерностей, которым подчинены случайные события и случайные величины, теория вероятности, как и любая другая наука, обращается к опыту – наблюдениям, измерениям, экспериментам. Результаты наблюдений за случайными величинами объединяются в наборы статистических данных. Задачей математической статистики, раздела современной теории вероятностей, является разработка методов сбора и обработки статистических данных, а также их анализа с целью установления законов распределения наблюдаемых случайных величин [8, 9].

1. Генеральная и выборочная совокупность данных

Генеральной совокупностью является набор всех мыслимых статистических данных, при наблюдениях случайной величины:

.

Наблюдаемая случайная величина Х называется признаком или фактором выборки. Генеральная совокупность есть статистический аналог случайной величины, ее объем N обычно велик, поэтому из нее выбирается часть данных, называемая выборочной совокупностью или просто выборкой

, .

Использование выборки для построения закономерностей, которым подчинена наблюдаемая случайная величина, позволяет избежать ее сплошного (массового) наблюдения, что часто бывает ресурсоемким процессом, а то и просто невозможным. Однако выборка должна удовлетворять следующим основным требованиям:

- выборка должна быть представительной, т.е. сохранять в себе пропорции генеральной совокупности,

- объем выборки должен быть небольшим, но достаточным для того, чтобы полученные результаты ее анализа обладали необходимой степенью надежности. В табл. 1 приводятся примеры генеральных и выборочных совокупностей.

Таблица 1

Генеральная совокупность	Выборочная совокупность
Данные переписи населения страны по разным признакам	Данные опроса случайных прохожих по тем же признакам
Времена работы электроламп, выпущенных заводом	Лабораторные данные о времени работы испытанных электроламп

Отметим, что в более строгом смысле выборку можно представить как многомерную случайную величину , у которой все компоненты распределены одинаково и по закону распределения наблюдаемой случайной величины. В этом смысле выборочные значения есть одна из реализаций величины .

2. Статистическое распределение выборки. Выборочный ряд, полигон, гистограмма и комулянта выборки

Возможные значения элементов выборки , называются вариантами выборки, причем число вариант m меньше чем объем выборки . Варианта может повторяться в выборке несколько раз, число повторения варианты в выборке называется частотой варианты . Причем . Величина называется относительной частотой варианты .

Упорядоченный по возрастанию значений набор вариант совместно с соответствующими им частотами называется вариационно-частотным рядом выборки:

; .

Ломаная линия, соединяющая точки вариационно-частотного ряда на плоскости или называется полигоном частот.

Пример 1. Пусть дана выборка полуденных температур месяца мая своим вариационно-частотным рядом, приведенным в табл. 2:

Таблица 2

хj	0	2	3	7	8	12	14	16	19	23	25	27	30
nj	1	1	1	1	5	6	2	2	5	2	1	3	1

На рис.10.1 приводится полигон частот рассматриваемой выборки.

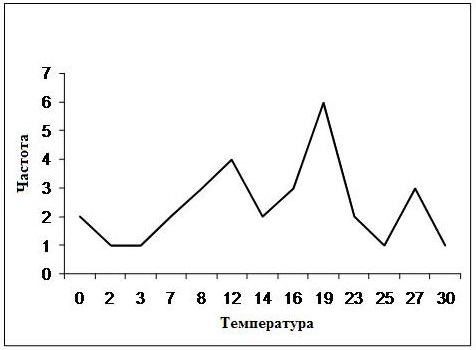
Рис.10.1 Полигон частот

Вариационно-частотный ряд имеет существенный недостаток, а именно, ненаглядность полигона в случае малой повторяемости вариант, например, при наблюдении непрерывного признака его повторяемость в выборке маловероятна. Более общей формой описания элементов выборки, является гистограмма выборки. Для ее построения, разобьем интервал значений выборки на m интервалов длины с границами . Число элементов выборки , попадающих в интервал, называется частотой интервала, кроме того вводятся следующие величины:

~ относительная частота интервала,

_j ~ плотность относительной частоты интервала.

Совокупность интервалов, наблюдаемой в выборке случайной величины и соответствующих им частот, называется гистограммой выборки.

, ,

Для частот гистограммы выполнены следующие условия нормировки:

, ,

Число интервалов гистограммы m должно быть оптимальным, чтобы, с одной стороны, была достаточной повторяемость интервалов, а с другой стороны не должны сглаживаться особенности выборочной статистики. Рекомендуется значение . На плоскости гистограмма представляется ступенчатой фигурой.

Пример 2. Наблюдаемые значения полуденной температуры месяца мая разбиты на 5 интервалов, соответствующая гистограмма задана следующей табл. 3:

Таблица 3

hj	0-5	5-10	10-15	15-20	20-25	25-30
nj	4	5	6	9	3	4

Гистограмма наблюдаемых температур приводится на рис. 10.2.

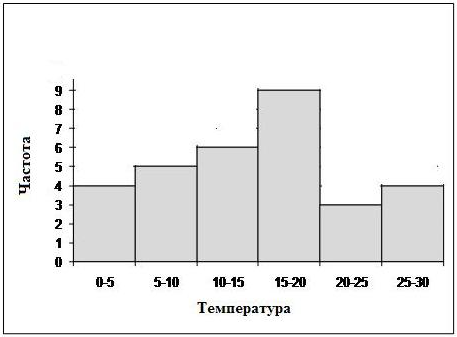
Рис. 10.2 Гистограмма частот

Выборочной или эмпирической функцией распределения называется функция , определяющая для каждого значения х относительную частоту события {X<x} в выборке, которая вычисляется через сумму соответствующих частот:

.

В нашем примере выборочная функция распределения (иногда называемая комулянтой) приводится на рис.10.3.

При увеличении объема выборки относительная частота события приближается к вероятности этого события (теорема Бернулли), поэтому выборочная функция распределения является оценкой теоретической функции распределения для случайной величины .

для любого х и .

Это утверждение строго доказано и носит форму теоремы Гливенко [7].

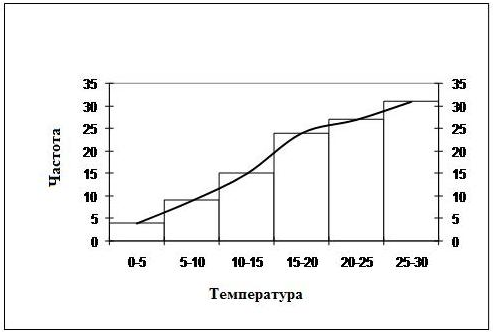
Рис. 10.3 Комулянта частот