3. О множественной регрессии

На практике, объясняемая переменная часто зависит не от одной, а нескольких объясняющих переменных . Пусть таких переменных будет , и они наблюдаются вместе с переменной в многофакторной выборке объема n. Построим выборочную линейную регрессию в форме:

.

Если введем следующие вектора , , то ее можно записать в векторном виде:

.

Введем матрицу измерений , вектор измерения и переменных , а так же вектор регрессии :

, , , ,

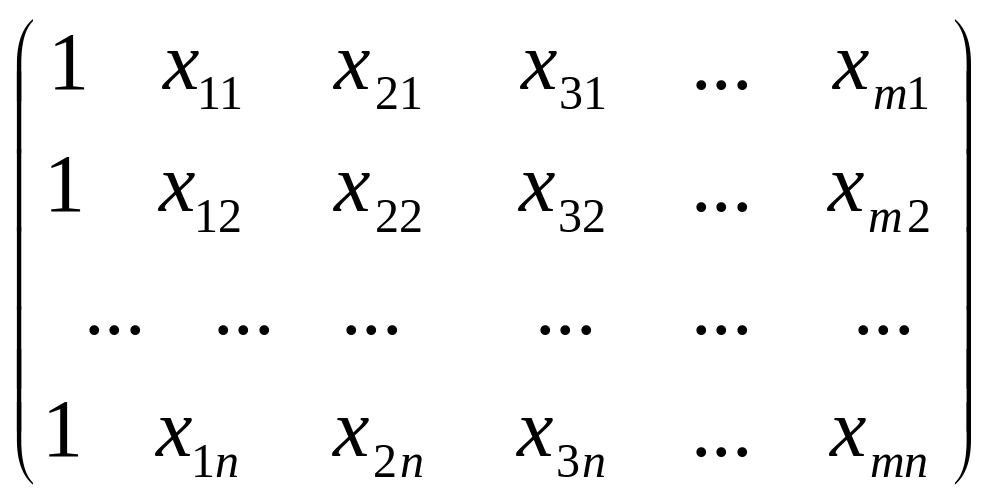Тогда, вектор регрессии будет , а ошибки регрессии .

Построим оценки коэффициентов регрессии методом наименьших квадратов, для чего рассмотрим суммарную ошибку регрессии

.

Подберем такие коэффициенты , при которых суммарная ошибка регрессии минимальна, для этого рассмотрим условие минимума:

, .

Таким образом, оценка для коэффициентов регрессии - построена. Матрица, входящая в выражение для коэффициентов имеет вид средних перекрестных произведений:

, .

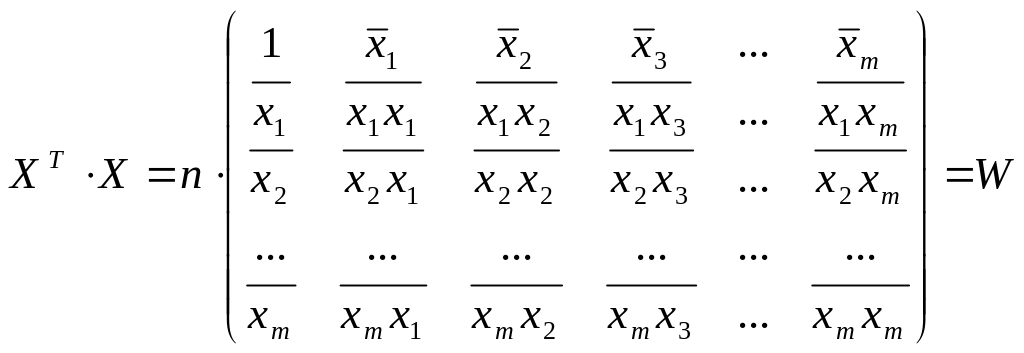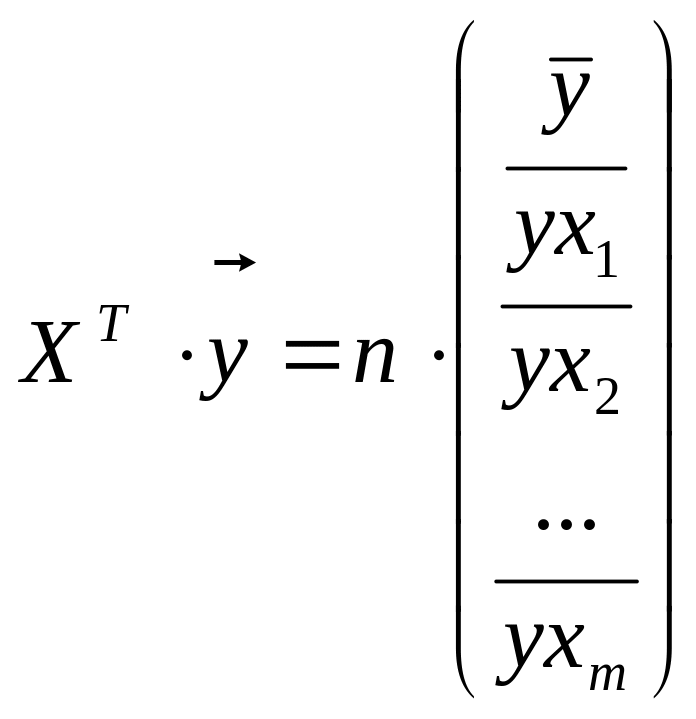Значимость построенного уравнения линейной среднеквадратической регрессии проверяется по значимости коэффициентов регрессии или коэффициента детерминации . Для проверки вычисляются: - дисперсия ошибок регрессии, - несмещенная стандартная ошибка регрессии, - несмещенные дисперсии коэффициентов регрессии. Для построения критериев значимости воспользуемся известными статистиками:

~ распределение Стьюдента с степенями свободы,

~ F-распределение Фишера с степенями свободы. Задаваясь уровнем значимости проверяемой гипотезы , соответствующей независимости величин и , можно сравнить наблюдаемое значение критерия , с критическим значением . Если , то гипотеза принимается, что говорит о незначимости коэффициента , мало отличного от нуля, то есть о незначимости переменной в уравнении регрессии, такие переменные желательно исключить из модели регрессии. Аналогично проверяется гипотеза о значимости коэффициента детерминации , соответствующей значимости всего уравнения регрессии в целом. Сравнивая наблюдаемое значение критерия , с критическим значением , можно утверждать, что если , то гипотеза принимается, что говорит о незначимости коэффициента , мало отличного от нуля, то есть о не значимости уравнения регрессии в целом.

Помимо значимости построенного уравнения регрессии, его качество оценивается так же отсутствием зависимости между объясняющими переменными (мультиколлинеарности), отсутствием зависимости величины дисперсии ошибок от переменных и (гетероскедастичности), отсутствием зависимости ошибок между собой (например, автокорреляции).

Мультиколлинеарность приводит к неустойчивости обращения матрицы W, а ее устранение возможно путем исключения из регрессионной модели малозначимых и сильнозависимых объясняющих переменных (факторов). Для этого исключения построим корреляционную матрицу парных коэффициентов корреляции: . Тогда, если , а коэффициент незначим или малозначим, то переменную можно исключить из модели регрессии, если коэффициент детерминации при этом значимо не уменьшается.

Гетероскедастичность и автокорреляция могут быть установлены при помощи теста ранговой корреляции Спирмена и теста Дарбина-Уотсона соответственно [1]. Влияние этих нежелательных для качества регрессии факторов может быть ослаблено путем различного рода преобразования переменных регрессионной модели [9].