1. Проверка гипотез о значении параметров распределения

Пусть случайная величина распределена нормально по закону с неизвестными параметрами и наблюдается в выборке объема n. Нормальный закон распределения задается следующей функцией плотности распределения вероятности:

, , .

По данным выборки могут быть получены выборочное среднее и выборочный стандарт :

= , = .

Эти величины являются случайными и по ним могут быть построены оценки математического ожидания и дисперсии наблюдаемой в выборке случайной величины Х.

Ниже проверим ряд простых статистических гипотез об истинных значениях параметров нормальной случайной величины .

1.1. . Проверим сначала гипотезу о равенстве значения истинного (гипотетического) математического ожидания а некоторой величине . Основная гипотеза тем самым будет следующей . В качестве критерия возьмем случайную величину имеющую, при справедливости основной гипотезы, распределение Стьюдента с n-1 степенями свободы:

Задаваясь уровнем значимости для проверяемой гипотезы , будем строить критическую область в зависимости от вида единственной конкурирующей (альтернативной) гипотезы в следующих случаях:

Случай А: . В этом случае, при справедливости конкурирующей гипотезы ожидаем сдвиг вероятных значений критерия в большую сторону (рис.14.1), поэтому критическая область критерия будет правосторонней . Критическая точка однозначно определяется из условия равенства вероятности ошибки I-рода заданному уровню значимости . Решение этого уравнения представляет собой правостороннюю квантиль распределения случайной величины Стьюдента и приводится таблицей в приложении 3.

Рис. 14.1 Критические области гипотезы .

Случай Б: . В этом случае, критическая область критерия будет левосторонней , а значения критерия отрицательными (рис.14.1). Критическая точка определяется из уравнения , решение которого, в силу симметрии распределения Стьюдента, будет следующим .

Случай В: . В этом случае критическая область критерия будет двухсторонней . Однако, здесь критические точки не определяются однозначно из уравнения . Доказано [9], что при условии и мощность критерия по отношению к конкурирующей гипотезе Н₁ будет максимальной. Тогда из этих уравнений критические точки находятся однозначно и представляют собой двухстороннюю квантиль распределения случайной величины Стьюдента:

, .

Рассмотрим числовой пример: Пусть по выборке объема n=16 получена оценка математического ожидания наблюдаемой нормальной случайной величины и оценка среднеквадратического отклонения . Поскольку, каждая оценка есть величина случайная (получена по конкретной случайной выборке), то проверим гипотезу о том, что истинное математическое ожидание наблюдаемой величины равна 15 т.е. . Зададимся уровнем значимости гипотезы и альтернативной гипотезой . Наблюдаемое в выборке значение критерия . Критическая область двухсторонняя, а критические точки будут:

; .

Видим, что принадлежит критической области и значит, гипотеза отвергается, т.е. отличие наблюдаемого значения математического ожидания от гипотетического значительны.

1.2. Проверим теперь гипотезу о том, что истинная (гипотетическая) дисперсия случайной величины равна . Проверяемая гипотеза В качестве критерия возьмем одномерную случайную величину , имеющую распределение «хи-квадрат» с n-1 степенями свободы:

.

Здесь оценка , полученная по выборке .

Задаваясь уровнем значимости для проверяемой гипотезы , будем строить критическую область в зависимости от вида единственной конкурирующей (альтернативной) гипотезы H₁ в следующих случаях (рис.14.2):

Случай А: . В этом случае, при справедливости конкурирующей гипотезы ожидаем сдвиг наиболее вероятных значений критерия в большую сторону, поэтому критическая область будет правосторонней.

Рис. 14.2 Критические области гипотезы .

Критическая точка здесь однозначно определяется согласно общего подхода к построению критических областей критерия из условия равенства вероятности ошибки I-рода заданному уровню значимости :

Решение этого уравнения находятся однозначно, и представляет собой правостороннюю квантиль «хи-квадрат» распределения случайной величины и приводится в приложении 4.

Случай Б: . В этом случае критическая область критерия будет левосторонней, а критическая точка однозначно определяется из уравнения :

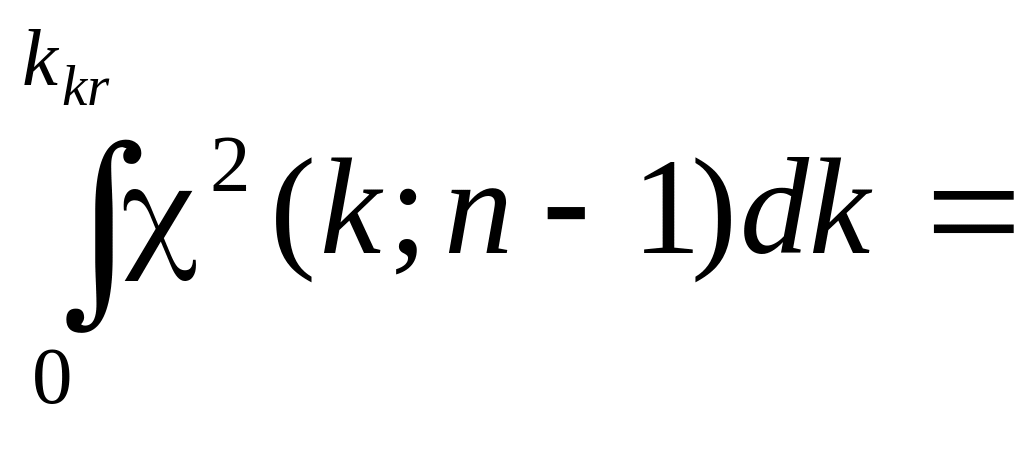
Левосторонняя критическая точка может быть легко выражена через функцию для правосторонней критической точки. Действительно, т.к. , то и тогда решение для левосторонней точки будет следующим .

Случай В: . В этом случае, объединяющем два предыдущих случая, критическая область критерия будет двухсторонней . Однако, здесь критические точки не определяется однозначно из уравнения

.

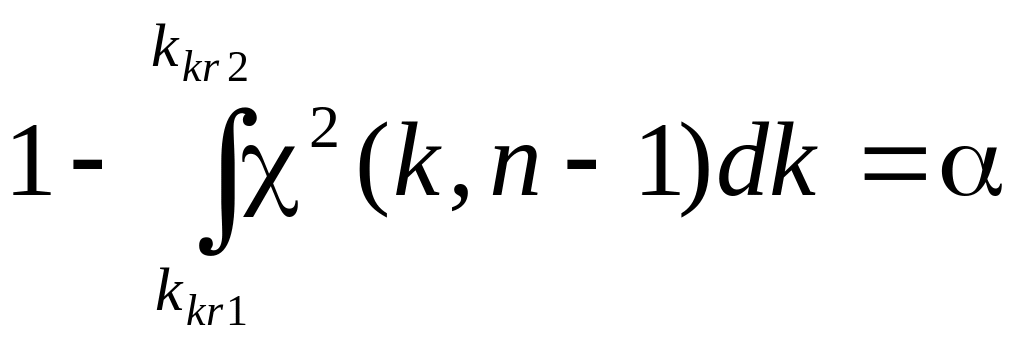Доказано [9], что при условиях мощность критерия по отношению к конкурирующей гипотезе будет максимальной, тогда из этих двух условий критические точки находятся однозначно:

; .

Рассмотрим числовой пример: Пусть по выборке объема n=15 получена оценка дисперсии наблюдаемой нормальной случайной величины или оценка среднеквадратического отклонения . Поскольку, каждая оценка есть величина случайная (получена по конкретной случайной выборке), то проверим гипотезу о том, что истинная дисперсия наблюдаемой величины равна 36, т.е. . Зададимся уровнем значимости гипотезы и альтернативной гипотезой .

Наблюдаемое значение критерия . Критическая область двухсторонняя, а критические точки будут:

Видим, что не принадлежит критической области и значит, гипотеза принимается, т.е. отличия наблюдаемого значения дисперсии от гипотетического незначительны. Если бы, такая оценка дисперсии была получена по выборке меньшего объема n=7, то

тогда наблюдаемое значение критерия попадает в критическую область и тогда проверяемая гипотеза отвергается.

Отметим, что при проверке гипотез и при уровне значимости будут построены двухсторонние критические области такими, что область принятия гипотез совпадет с доверительными интервалами, построенными с надежностью .