2. Центральная предельная теорема
Это на самом деле группа теорем, устанавливающих связь с нормальным законом распределения величины с функцией плотности распределения вероятности (рис. 9.1):
,
где
,
параметры распределения.
Рис. 9.1. Плотность распределения нормальной случайной величины
Приведём формулировку одной из таких теорем (приводим без доказательства).
Теорема Ляпунова. Если:
а) - независимые случайные величины;
б) существуют
и
для всех
;
в) существуют
величины
и
,
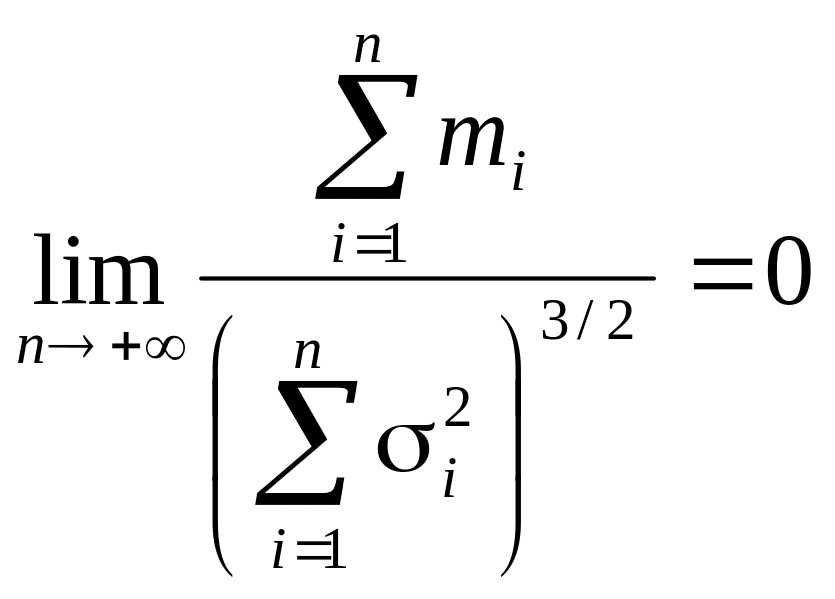то закон
распределения величины
(при
)
неограниченно приближается к нормальному
закону с математическим ожиданием
и дисперсией
,
т.е.:
,
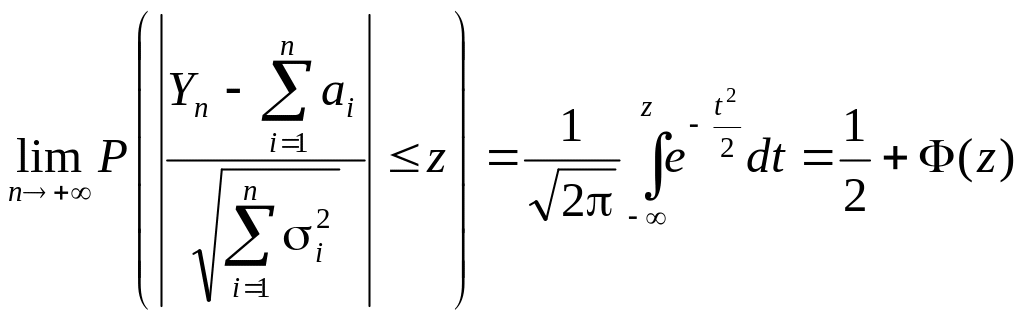где
есть известная нам функция Лапласа.
Смысл теоремы состоит в том, что чем сложней случайная величина, чем больше факторов, влияющих на ее значение, тем ближе она к нормально распределенной случайной величине.
Следствие. Если независимые случайные величины имеют одинаковые математические ожидания и дисперсии
,
,
и существуют
величины
,
то закон распределения величины
при неограниченно приближается к нормальному закону с теми же параметрами и .
________________________
Пример. Пусть - потребление электроэнергии жильцами квартиры номер в многоквартирном, многоэтажном доме. Тогда по теореме Чебышева среднее потребление:
,
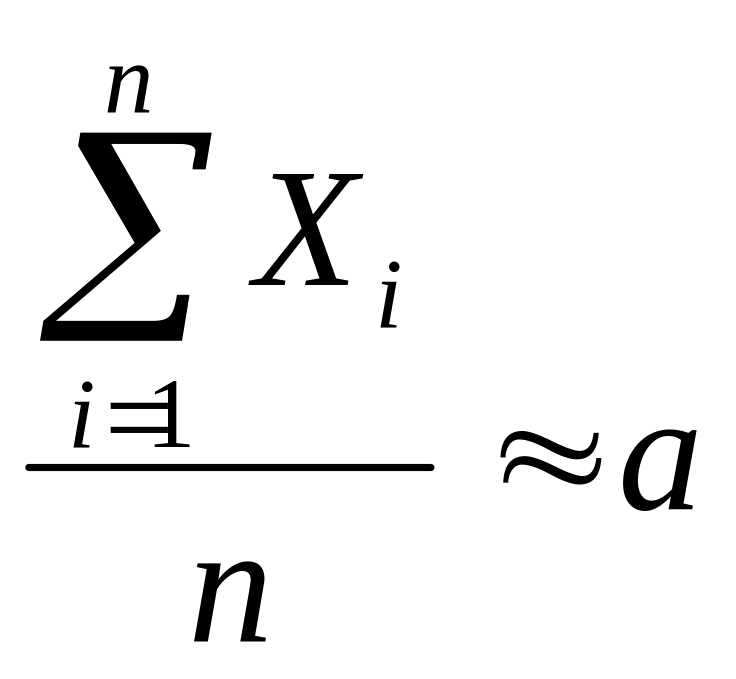а по теореме Ляпунова величина:
является случайной величиной, имеющей нормальный закон распределения (т.е. будет отличаться от величины , как нормально распределённая случайная величина).
________________________
Пример.
Представим величину Бернулли
(количество наступления события
в серии из
испытаний)
в виде суммы независимых величин, так
называемых «индикаторов» каждого из
испытаний:
.
Здесь - случайные величины - «индикаторы испытания»:
|
1 |
0 |
|
|
|
,
.
Тогда по свойствам
математического ожидания и дисперсии
случайная величина Бернулли
будет иметь следующие параметры:
,
,
,
а в соответствии
с центральной предельной теоремой при
большом количестве испытаний (
),
она будет иметь распределение, близкое
к нормальному, с параметрами
и
:
.
3. Теорема Бернулли
Важнейшее методологическое значение для теории вероятностей и математической статистики имеет следующая теорема о частоте события. В серии испытаний Бернулли частоту события определим как:
.
Теорема Бернулли.
Если количество испытаний велико, то частота события в испытании является нормальной случайной величиной с математическим ожиданием, равным вероятности события.
Действительно,
поскольку частота события
в силу
центральной теоремы при
является величиной нормальной, а в силу
основных свойств математического
ожидания и дисперсии имеет
математическое ожидание
и дисперсию
.
В соответствии с формулами Муавра – Лапласа, величина отклонения частоты и вероятности события имеет следующую вероятность:
для любого .
Таким образом, с ростом количества испытаний частота события стремится к его вероятности.