
- •1.1.2 Общая постановка большинства задач оптимизации:
- •1.1.3. По виду решаемой задачи можно выделить следующие разделы мп:
- •1.1.4. Определение задачи линейного программирования. (злп)
- •1.2. Графоаналитический метод для решения задачи линейного программирования (злп).
- •Двойственная задача в лп.
- •1.3.1 Правила и особенности перехода к двойственной задаче.
- •1.3.2. Теоремы двойственности.
- •1.3.3. Экономический смысл переменных двойственной задачи.
- •1.4. Свойства двойственных оценок оптимального объемного планирования производства.
- •1.4.1 Свойства:
Математическое программирование
1.1. Понятие о математическом программировании (МП).
Классификация методов МП.
МП - раздел прикладной математики, изучающий способы оптимизации, т.е. совершенствования и повышения эффективности организации, планирования и управления организацией в различных системах на основе вычислительных методов, т.е. в основе МП лежит математический аппарат решения задач оптимизации.
1.1.1. Некоторые приложения МП:
1. в исследовании операции
1.1 оптимизация технико-экономических систем, транспортные задачи
1.2 управление запасами
2. в автоматике
2.1 распознавание систем
2.2 оптимальное управление системами
2.3 управление производством
3. в технике
3.1 определение оптимальных размеров
3.2 оптимальное планирование информационных систем
3.3 планирование ЭВМ-сетей
4. в математической экономике
4.1 решение больших макроэкономических моделей
4.2 решение моделей (задач) предпринимательства
4.3 теория принятия решений
Постановка любой задачи оптимизации начинается с определения набора независимых переменных и обычно включает условия, которые характеризуют их приемлемые значения (ограничение задач).
Обязательным компонентом описания задачи является мера качества (функция, зависящая от переменных) - целевая функция.
Под оптимальностью понимают максимальность или минимальность целевой функции.
1.1.2 Общая постановка большинства задач оптимизации:
Найти max f(x),min f(x) = f(x*) = f*
x принадлежит X (хХ)
x = [x1...xn]T - векторная переменная, по которой ведется оптимизация.
[]T- означает транспонирование.
X - некоторое допустимое множество (область) ограничений или условий.
f(x) - скалярная функция векторного аргумента, заданная на множестве Х; целевая функция; критерий оптимальности; оптимизированная функция.
f*-минимальное, максимальное значение функции (решение задачи).
х*- значение аргумента, при котором достигается f*.
Множество условий Х чаще всего имеет вид:
![]() ,
,
![]() (1.1)
(1.1)
![]() -
функции ограничений.
-
функции ограничений.
![]() (1.2)
(1.2)
![]() -знак
принадлежности
-знак
принадлежности
R-
заключено в пределах от -
до +,
![]() .
.
Во
многих случаях важно различать ограничения
неравенства и ограничения равенства
(![]() ;
;
![]() ).
).
1.1.3. По виду решаемой задачи можно выделить следующие разделы мп:
1. линейное программирование (ЛП) - это раздел МП, изучающий задачу определения min или мах линейной функции многих переменных, при линейных ограничениях в виде равенств или неравенств.
2 нелинейное программирование (НП) - это раздел МП, изучающий методы отыскания экстремумов в задачах оптимизации с нелинейной целевой функцией и/или нелинейными ограничениями.
3. стохастическое программирование (случайность) - изучает методы выбора оптимальных решений в ситуациях характеризуемых случайными величинами.
4. целочисленное программирование - изучает методы решения задач оптимизации, в которых на значение всех или части переменных целевой функции наложено требование целочисленности.
5. динамическое программирование - изучает методы для решения оптимизационных задач, в которых необходимо рассмотреть процесс производства в развитии.
6. параметрическое программирование - изучает оптимизацию систем, в моделях которых коэффициенты целевой функции или ограничений не являются постоянными величинами, а изменяются из-за различных факторов.
1.1.4. Определение задачи линейного программирования. (злп)
ЗЛП состоит в максимизации (минимизации) линейной функции при линейных ограничениях.
Пример 1.1:
найти
![]() (1.3)
(1.3)
при ограничениях:
 (1.4)
(1.4)
ЗЛП, записанная в виде (1.3) и (1.2), называется общей задачей ЛП, заданной в произвольной форме записи.
Любую ЗЛП можно записать в виде:
найти
при
условиях
![]() , но при этом вводится дополнительное
условие:
, но при этом вводится дополнительное
условие:
![]() (1.5)
(1.5)
(1.3) и (1.5) - стандартная форма записи ЗЛП
Любую ЗЛП можно представить в виде:
найти (1.6)
при
 (1.7)
(1.7)
(1.6) и (1.7) - представляют собой каноническую форму записи ЗЛП.
ЗЛП в произвольной постановке всегда может быть приведена к стандартной и канонической формам с помощью следующих преобразований ( - знак преобразования):
 ; (1.8)
; (1.8)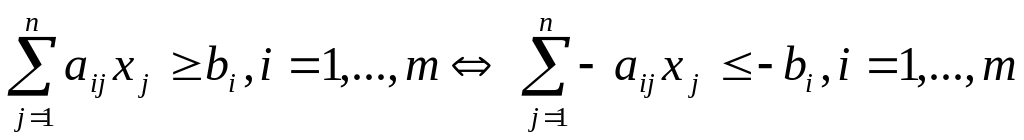 ; (1.9)
; (1.9)если
 ,
то
,
то
 ; (1.10)
; (1.10) ; (1.11)
; (1.11)
![]() ~
- означает, что эту переменную дополнительно
вводят.
~
- означает, что эту переменную дополнительно
вводят.
 (1.12)
(1.12)
Преобразования 3-5 приводят к увеличению размера задачи.
Пример 1.2:
![]()

В стандартной форме:
![]()

В канонической форме:

