Задача № 4.4
Построить
характеристику и определить критический
угол поперечной устойчивости трактора
или автомобиля
при заданной скорости движения
и заданному радиусу поворота
по стерне нормальной влажности. При
расчёте характеристики
значением инерционного момента от
вращения деталей, расположенных в
продольной плоскости, пренебречь.
Варианты задания приведены в таблице 4.4.
Таблица 4.4
№ вар. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Марка трактора |
Т- 25А1 |
Т- 28Х4 |
Т- 40М |
Т- 40АМ |
МТЗ- 50 |
МТЗ- 80 |
МТЗ- 82 |
Т- 150К |
№ вар. |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Марка трактора |
К- 701 |
ЛТЗ- 145 |
ДТ- 75М |
ДТ- 75С |
Т- 150 |
Т- 70С |
Т- 4А |
Т- 130 |
№ вар. |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
Марка автомоб. |
М 2140 |
ГАЗ 21 |
ГАЗ 24 |
ГАЗ 53 |
ГАЗ 66 |
ЗИЛ 130 |
ЗИЛ 157 |
КрАЗ 214Б |
№ вар. |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
Марка автомоб. |
МАЗ 500 |
МАЗ 535 |
КамАЗ 5410 |
ВАЗ 2105 |
ВАЗ 2106 |
ВАЗ 2108 |
ВАЗ 2110 |
УАЗ 469 |
Примечание:
для вариантов с 1-го по 16-ый скорость
движения
,
радиус поворота
;
для вариантов с 17-го по 32-ой скорость
движения
,
радиус поворота
.
Решение задачи
выполним для трактора МТЗ-142, движущегося
со скоростью
на повороте с радиусом
по стерне нормальной влажности. Вес
трактора
;
ширина колеи
;
ширина колеса
;
высота центра тяжести
выбираются по справочной литературе.
Условие поперечной устойчивости трактора при заданных условиях движения имеет вид
.
Правая часть
этого неравенства, обозначенная как
функция
,
при известных параметрах трактора
зависит только от угла
.
Задавая различные значения угла
,
можно рассчитать и построить график
функции
.
Для заданных условий движения график
функции
представлен на рис. 4.2. Этот график
называют характеристикой поперечной
устойчивости автомобиля или трактора.
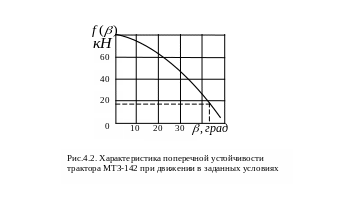
Составляющая центробежной силы, действующая в поперечной плоскости при повороте, определяется по формуле:
.
Откладывая
полученное значение составляющей
центробежной силы
по оси ординат характеристики поперечной
устойчивости трактора, проводим линию
параллельную оси абсцисс до пересечения
с кривой
.
Точку пересечения проектируем на ось
абсцисс и по шкале угла
определяем критический угол поперечной
устойчивости трактора МТЗ-142 при движении
в заданных условиях, величина которого
равна
.
Определим предельный угол статической поперечной устойчивости трактора МТЗ-142
.
Так как
,
то значение критического угла поперечной
устойчивости, при котором станет
возможным опрокидывание трактора
МТЗ-142 в заданных условиях движения,
равно
.
Задача № 4.5
Определить
предельную по сцеплению величину боковой
реакции дороги, действующей на колесо,
если оно движется по дороге с коэффициентом
сцепления
и нагружено нормальной силой
.
Известно, что величина этой реакции
составляет четвёртую часть толкающей
реакции
.
Ответ:
.
Задача № 4.6
Автомобиль
движется прямолинейно по косогору с
толкающей реакцией
.
Найти предельные по опрокидыванию и
сцеплению (боковому скольжению) углы
косогора, если ширина колеи
;
высота центра тяжести
;
коэффициент сцепления колёс с дорогой
.
На сколько процентов следует уменьшить
высоту центра тяжести, чтобы углы были
равны между собой?
Ответ:
.
Задача № 4.7
Определить
сможет ли автомобиль двигаться на
косогоре с углом
без опрокидывания и бокового скольжения,
если ширина колеи автомобиля
;
высота центра тяжести
,
а коэффициент сцепления колёс с дорогой
.
Ответ: не сможет.
Задача № 4.8
Автомобиль
движется в установившемся режиме по
горизонтальному криволинейному участку
пути радиуса
.
Определить скорости движения, при
которых произойдёт опрокидывание и
занос автомобиля, если ширина колеи
автомобиля
;
высота центра тяжести
,
а коэффициент сцепления колёс с дорогой
.
При какой величине коэффициента сцепления
эти скорости будут равны.
Ответ:
.
Задача № 4.9
Определить с
какой максимальной скоростью может
двигаться автомобиль на повороте с
радиусом
без опрокидывания в поперечной плоскости,
если ширина колеи автомобиля
,
а высота центра тяжести
.
Ответ:
.
Задача № 4.10
Определить по
условию поперечного опрокидывания
скорости гружёного и негружёного
автомобиля при движении на повороте с
радиусом
,
если ширина колеи автомобиля
,
высота центра тяжести у автомобиля без
груза
,
а гружёного -
.
На сколько процентов они отличаются
друг от друга?
Ответ:
.
Задача № 4.11
Определить по
условию бокового опрокидывания
минимальный радиус поворота, с которым
может двигаться автомобиль на
горизонтальном участке пути со скоростью
,
если ширина колеи автомобиля
,
а высота центра тяжести
.
Найти значение коэффициента сцепления
,
при котором начнётся занос автомобиля,
движущегося по этому участку пути.
Ответ:
.
Задача № 4.12
Будет ли возможным боковое опрокидывание автомобиля, движущегося на повороте по дороге с коэффициентом сцепления , если ширина колеи автомобиля , а высота центра тяжести . Какой величиной должна быть высота центра тяжести, чтобы автомобиль не опрокидывался при движении по дороге с коэффициентом сцепления ?
Ответ:
невозможно;
.
Задача № 4.13
С каким
минимально возможным радиусом поворота
может двигаться автомобиль без потери
устойчивости по скольжению и опрокидыванию
со скоростью
на горизонтальном участке пути с
коэффициентом сцепления
,
если ширина колеи автомобиля
,
а высота центра тяжести
?
Ответ:
.
Задача № 4.14
Рассчитать
значение коэффициента сцепления
,
при котором автомобиль, движущийся по
горизонтальному участку пути на повороте
радиусом
со скоростью
,
получит боковое скольжение. Определить
ширину колеи автомобиля при движении
по дороге с коэффициентом сцепления
,
при которой не произойдёт его опрокидывание,
если высота центра тяжести автомобиля
.
Ответ:
.
Задача № 4.15
Определить
высоту центра тяжести автомобиля,
движущегося на повороте радиусом
со скоростью
,
при которой произойдёт опрокидывание
автомобиля, если ширина колеи автомобиля
.
При каких значениях коэффициента
сцепления
это станет возможным?
Ответ:
.
Задача № 4.16
На сколько
процентов изменится скорость, при
которой происходит опрокидывание
автомобиля, если при движении автомобиля
на повороте с радиусом
без груза высота центра тяжести
,
а с грузом -
.
Ширина колеи автомобиля
.
Ответ:
на
.
Задача № 4.17
Возможно ли опрокидывание грузового автомобиля, движущегося со скоростью на повороте с радиусом на горизонтальном участке пути, если ширина колеи автомобиля , а высота центра тяжести .
Ответ: невозможно.
Задача № 4.18*
С какой
максимальной скоростью может двигаться
легковой автомобиль на косогоре с углом
поперечного уклона
,
совершающий поворот с радиусом
в сторону уклона, если ширина колеи
автомобиля
,
а высота центра тяжести
?
Определить угол поперечного уклона
,
при котором опрокидывание невозможно
на любой скорости движения.
Ответ:
.
Задача № 4.19*
Грузовой автомобиль движется по косогору с углом поперечного уклона со скоростью и совершает поворот с радиусом в сторону уклона по дороге с коэффициентом сцепления . Толкающая реакция . Определить минимальный угол поперечного уклона , при котором ещё возможно движение автомобиля без заноса.
Ответ:
.
Задача № 4.20*
Определить минимальный угол косогора , на котором автомобиль, двигаясь со скоростью и совершая поворот с радиусом в сторону уклона по дороге с коэффициентом сцепления , будет иметь устойчивое движение без опрокидывания и заноса, если ширина колеи автомобиля , а высота центра тяжести . Толкающая реакция .
Ответ:
.
Задача № 4.21*
Автомобиль
совершает поворот радиусом
на косогоре с углом наклона
в сторону уклона. Определить максимальную
скорость, с которой может двигаться
автомобиль без опрокидывания и заноса,
если ширина колеи автомобиля
,
высота центра тяжести
,
а коэффициент сцепления колёс с дорогой
.
Толкающая реакция
.
Ответ:
.
Задача № 4.22
Автомобиль совершает поворот радиусом на горизонтальном участке пути с коэффициентом сцепления . Определить угол поперечного уклона, при повороте на котором с радиусом критическая скорость по боковому скольжению равна критической скорости при движении на горизонтальном участке пути. Толкающая сила .
Ответ:
.
Задача № 4.23
Определить
критическую скорость по боковому
скольжению автомобиля, совершающего
поворот с радиусом
на косогоре с углом поперечного уклона
в сторону уклона по дороге с коэффициентом
сцепления
.
Как следует изменить угол поперечного
уклона, чтобы критическая скорость
выросла вдвое? Толкающая сила
.
Ответ:
увеличить на
.
Задача № 4.24
Автомобиль
движется на косогоре с углом поперечного
уклона
и совершает поворот с радиусом
в сторону подъёма. Определить критическую
скорость движения автомобиля по
опрокидыванию, если ширина колеи
автомобиля
,
а высота центра тяжести
.
Ответ:
.
Задача № 4.25
Переднеприводный
автомобиль массой
движется по косогору по дороге с
коэффициентом сцепления
и развивает касательную силу тяги
.
Определить угол поперечного уклона,
при котором произойдёт занос ведущей
оси, если база автомобиля
,
а расстояние от центра тяжести до задней
оси
.
Ответ:
.
Задача № 4.26
Грузовой
автомобиль массой
движется со скоростью
на криволинейном горизонтальном участке
пути радиуса
по дороге с коэффициентом сцепления
и развивает касательную силу тяги
.
Определить запас автомобиля по скорости
до наступления заноса задней ведущей
оси. База автомобиля
,
а расстояние от центра тяжести до оси
передних колёс
.
Составляющей центробежной силы в
продольной плоскости автомобиля
пренебречь.
Ответ:
.
Задача № 4.27
Определить
минимальный радиус поворота, на котором
может двигаться автомобиль массой
по горизонтальному участку пути со
скоростью
без бокового скольжения задней ведущей
оси. Касательная сила тяги, развиваемая
автомобилем
.
База автомобиля
,
расстояние от центра тяжести до передней
оси
,
а коэффициент сцепления колёс с дорогой
.
Ответ:
.
Задача № 4.28*
Переднеприводный
автомобиль массой
движется по окружности радиуса
на горизонтальном участке пути с
коэффициентом сцепления
и коэффициентом сопротивления качению
.
Определить критические скорости по
заносу передней и задней оси автомобиля,
если в статическом положении на переднюю
ось приходится
массы автомобиля, а фактор сопротивления
воздуха
.
Составляющую центробежной силы,
действующую в продольной плоскости
автомобиля, не учитывать.
Ответ:
.
Задача № 4.29
Автомобиль
движется равномерно на подъём с углом
на малой скорости. Существует ли опасность
его опрокидывания назад, если база
автомобиля
,
расстояние от центра тяжести до передней
оси
,
а высота центра тяжести
.
Сопротивлением качению автомобиля
пренебречь.
Ответ: такой опасности нет.
Задача № 4.30*
Автомобиль,
двигаясь со скоростью
на горизонтальном участке пути, совершает
поворот с радиусом
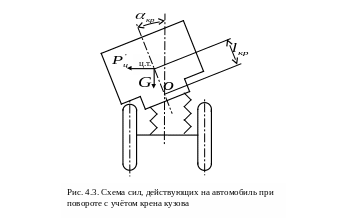
(рис. 4.3). Определить угол крена кузова
автомобиля
,
если подрессоренная масса
,
угловая жёсткость подвески
,
а плечо крена
.
Жёсткость шин не учитывать. На рисунке
4.3 точка
является осью крена.
Ответ:
.
Задача № 4.31*
Автомобиль
движется равномерно по окружности
радиуса
со скоростью
(рис. 4.3). Угол крена кузова автомобиля
.
Определить угловую жёсткость подвески
автомобиля, если подрессоренная масса
,
а плечо крена
.
Жёсткость шин не учитывать. На рисунке
4.3 точка
является осью крена.
Ответ:
.
Задача № 4.32*
Автомобиль
движется равномерно по окружности
радиуса
со скоростью
(рис.
4.3). Угол крена кузова автомобиля
.
Определить плечо крена кузова автомобиля,
если подрессоренная масса
,
угловая жёсткость передней подвески
,
а угловая жёсткость задней подвески
.
Жёсткость шин не учитывать. На рисунке
4.3 точка
является осью крена.
Ответ:
.
Задача № 4.33*
Определить
возможность опрокидывания автомобиля
массой
на косогоре с углом наклона
(рис. 4.3) с учётом бокового крена кузова
и без него (при блокированной подвеске),
если подрессоренная масса автомобиля
,
высота центра тяжести
,
ширина колеи
,
угловая жёсткость подвески
,
а плечо крена кузова
.
Жёсткость шин не учитывать.
Ответ: возможно; невозможно.
Задача № 4.34*
Определить
возможность опрокидывания грузового
автомобиля массой
на косогоре с углом наклона
с учётом бокового крена кузова (рис.
4.3), если подрессоренная масса автомобиля
,
ширина колеи
,
высота центра тяжести
,
угловая жёсткость подвески
,
а плечо крена кузова
.
Жёсткость шин не учитывать.
Ответ: невозможно.
Модуль 5
Задача № 5.1
Определить мощность, расходуемую трактором на буксование, и величину буксования движителей при установившемся движении трактора на горизонтальном участке пути со скоростью по стерне нормальной влажности в случае отсутствования ВОМ, если двигатель работает в номинальном режиме и нагрузка на крюке составляет половину номинального тягового усилия.
Варианты задания представлены в таблице 5.1.
Таблица 5.1
№ вар. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Марка трактора |
Т- 16М |
Т- 25А1 |
Т- 28Х4 |
Т- 40М |
Т- 40АМ |
МТЗ- 50 |
МТЗ- 80 |
МТЗ- 82 |
ЮМЗ- 6Л |
Т- 150К |
№ вар. |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Марка трактора |
К- 701 |
ЛТЗ- 145 |
ЛТЗ- 155 |
ДТ- 75М |
ДТ- 75С |
Т- 150 |
Т- 70С |
Т- 4А |
Т- 130 |
Т- 100М |
Решение задачи
выполним для трактора МТЗ-142 при заданных
условиях движения. Вес трактора
,
номинальная мощность двигателя
,
КПД, учитывающий потери в трансмиссии
,
номинальное тяговое усилие
и коэффициент сопротивления качению
выбираются по справочной литературе.
Определим действующую по условиям задачи силу тяги на крюке
.
Уравнение мощностного (энергетического) баланса трактора для заданных условий движения запишется
.
Учитывая, что
по условиям задачи
выразим из приведенного уравнения
мощность, расходуемую на буксование
.
Определим составляющие правой части выражения.
Мощность,
потерянная в трансмиссии
,
определяется по формуле:
.
Мощность,
затрачиваемая на преодоление сопротивления
качению
,
расчитывается по выражению
.
Мощность на крюке может быть определена по формуле:
.
Подставляя вычисленные величины мощностей в выражение для определения мощности, расходуемой на буксование, получим
.
Мощность, подводимую к ведущим колёсам трактора, можно определить по формуле:
.
С другой стороны мощность, расходуемая на буксование ведущих органов, определяется выражением
.
Из данного
выражения можно определить величину
буксования ведущих органов трактора,
используя рассчитанные значения
мощностей
и
.