2.3 Лабораторная работа «Корреляционный анализ»

Цель работы: получить навыки и умения измерения тесноты связи с помощью коэффициента корреляции и корреляционного отношения.

Задачи:

- изучить теоретические аспекты корреляционного анализа;

- используя пример выполнения лабораторной работы рассчитать коэффициент корреляции (таблица 2.16) и корреляционное отношение (таблица 2.17) – все значения Y изменить на величину своего варианта;

- ответить на контрольные вопросы.

Методический материал

2.3.1 Парная корреляция

Связи между различными явлениями в природе сложны и многообразны. Однако их можно определенным способом классифицировать. В технике и естествознании часто речь идет о функциональной зависимости между переменными X и Y, когда каждому значению X поставлено в однозначное соответствие определенного значения Y.

В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияние каждого из которых ничтожно, а число этих факторов велико. В этих случаях связь теряет свою строгую функциональность, и изучаемая физическая система переходит не в определенное состояние, а в одно из возможных. Здесь речь идет о стохастической связи. Частный случай стохастической связи – статистическая связь. Об этой связи имеет смысл говорить, когда условное математическое ожидание одной случайной переменной является функцией значения, принимаемого другой случайной переменной.

Значения статистической зависимости между случайными переменными имеет большое практическое значение. С ее помощью можно прогнозировать зависимость случайной переменной, в предположении, что независимая принимает определенное значение. Чтобы изучить статистическую зависимость необходимо знать условное математическое ожидание случайной переменной. Для его оценки необходимо знать аналитический вид двухмерного распределения (X;Y).

Корреляционная зависимость – это зависимость между одной случайной переменной и условным средним значением другой переменной.

Примерами корреляционной связи являются зависимости: между пределами прочности и текучести стали определенной марки, между погрешностью размера и погрешностью формы поверхности детали, обработанной определенным методом, межу температурой испытания и ударной вязкостью стали, между усилием прижима ролика и шероховатостью накатанной детали. В первых двух примерах имеет место корреляционная связь между двумя откликами, а в третьем и четвертом – между фактором, который является случайной величиной в связи с погрешностью измерения, и откликом.

Двумерная корреляция изучает пары случайных чисел. Эти числа можно изобразить графически в виде точки с координатами (X;Y). Таким образом, можно изобразить весь набор пар случайных чисел, т.е. всю выборку (примеры различных видов корреляции представлены на рисунке 2.15). Эта задача упрощается, если выборку упорядочить. Для этого значения X и Y разбивают на интервалы. По одной оси откладывают интервалы, соответствующие переменной Y, а по другой – соответствующие X. Каждую пару чисел изображают в виде точки в соответствующей клетке.

Такое изображение корреляционной зависимости называется полем корреляции (рисунок 2.16). По расположению точек можно в первом приближении предположить о форме и тесноте корреляционной связи.

Полная информация о вероятностной связи двух случайных величин представляется совместной плотностью распределения f(x;y) или условными плотностями распределения f(x/y), f(y/x), то есть плотностями распределения случайных величин X и Y при задании конкретных значений y и x соответственно.

Для независимых случайных величин совместная плотность распределения f(x, y) равна произведению плотностей распределения случайных величин X и Y:

f(x,y) = fx(x) fy(y). (2.56)

а) б)

в) г)

Рисунок 2.15 – Примеры различных видов корреляции: а) – идеальная линейная корреляция; б) – линейная корреляция с умеренным рассеянием; в) – нелинейная корреляция; г) – отсутствие корреляции (r – коэффициент корреляции)

Р исунок 2.16 – Поле корреляции

Основными характеристиками вероятностных зависимостей являются корреляционный момент и коэффициент корреляции.

Корреляционный момент (или момент связи) двух случайных величин X и Y-это математическое ожидание произведения центрированных случайных величин:

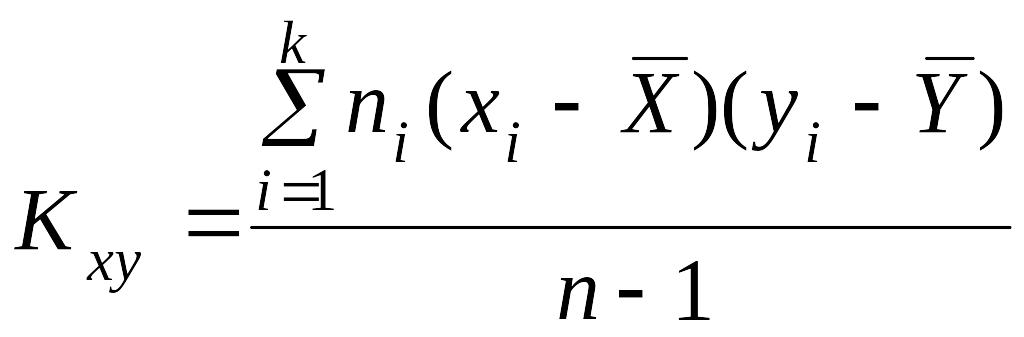, (2.57)

где и – математические ожидания случайных величин x и y.

Корреляционный момент одновременно характеризует связь между случайными величинами и их рассеивание. По своей размерности он соответствует дисперсии для независимой случайной величины.

Если случайные величины независимы, то корреляционный момент равен нулю, так как его можно представить как произведение центральных моментов случайных величин, которые равны нулю.

Если хотя бы одна из случайных величин имеет малое рассеяние, то корреляционный момент мал даже при явной зависимости между случайными величинами. Поэтому для выделения характеристики тесноты связи между случайными величинами переходят к коэффициенту корреляции r_xy:

, (2.58)

где Sx и Sy- средние квадратические отклонения случайных величин Х и Y.

Коэффициент корреляции можно вычислить, не прибегая к расчету средних квадратических отклонений, что упрощает вычислительную работу, по следующей аналогичной формуле:

(2.59)

или по формуле:

(2.60)

где D_x , D_y – суммы квадратов отклонений

, (2.61)

, (2.62)

Коэффициент корреляции, характеризуя степень тесноты связи случайных величин и может изменяться в пределах от -1 до +1. Чем ближе значение его абсолютной величины к единице, тем сильнее линейная связь между случайными величинами; чем ближе к нулю, тем эта связь слабее. При r_xy = 1 или r_xy = - 1 статистическая линейная связь становится функциональной. При значениях близких к нулю линейная корреляционная связь отсутствует. Для независимых случайных величин также r_xy= 0.

При более подробном анализе вероятностной связи определяют условные математические ожидания случайных величин, то есть математические ожидания случайных величин Y и X при заданных конкретных значениях x и y соответственно.

Коэффициент корреляции служит для измерения только линейной связи. Для измерения нелинейной зависимости между переменными X и Y используют предложенный К. Пирсоном показатель, который называют корреляционным отношением. Данный показатель является универсальным - он позволяет характеризовать любую форму корреляционной связи (линейную и нелинейную) [2].

Коэффициент детерминации вычисляется по формуле:

, (2.63)

где - межгрупповая дисперсия;

- общая дисперсия

(2.64)

(2.65)

Корреляционное отношение вычисляется по формуле:

, (2.66)

Пример выполнения лабораторной работы

1 Группируем первичные данные в виде таблицы для расчета коэффициента корреляции (таблица 2.16):

Таблица 2.16 – Данные для расчета коэффициента корреляции

Xi	Yi	XiYi	X2i	Y2i
10,0	0,70	7,000	100,00	0,4900
10,8	0,73	7,884	116,64	0,5329
11,3	0,75	8,475	127,69	0,5625
10,0	0,70	7,000	100,00	0,4900
10,1	0,65	6,565	102,01	0,4225
11,1	0,65	7,215	123,21	0,4225
11,3	0,70	7,910	127,69	0,4900
10,2	0,61	6,222	104,04	0,3721
13,5	0,70	9,450	182,25	0,4900
12,3	0,63	7,749	151,29	0,3969
14,5	0,70	10,150	210,25	0,4900
11,0	0,65	7,150	121,00	0,4225
12,0	0,72	8,640	144,00	0,5184
11,8	0,69	8,142	139,24	0,4761
13,4	0,78	10,452	179,56	0,6084
11,4	0,70	7,980	129,96	0,4900
12,0	0,60	7,200	144,00	0,3600
15,6	0,85	13,260	243,36	0,7225
13,0	0,80	10,400	169,00	0,6400
12,1	0,75	9,075	146,41	0,5625
237,4	14,06	167,919	2861,60	9,9598

2 Определяем суммы квадратов отклонений по формулам:

3 Используя формулу определяем коэффициент корреляции:

Полученная величина указывает на наличие положительной средней силы корреляционной связи между исследуемыми признаками.

4 Группируем первичные данные в виде таблицы 2.17 для расчета корреляционного отношения:

Таблица 2.17 – Данные для расчета корреляционного отношения

Группа	Интервал	Xi	Yi
1	2	3	4
1	2,0-3,5	2,0	1,8
		3,0	3,8
		3,3	3,4
		3,3	3,3
		3,4	2,9
2	3,5-5,0	3,5	4,1
		3,9	5,4
		3,9	6,4
		4,0	4,2
		4,1	5,0
		4,5	4,6
		4,8	5,2
		4.9	5.3
3	5,0-6,5	5,1	5,8
		5,4	8,5
		5,6	4,6
		5,9	7,0
		5,9	9,0
		6,3	8,0
		6,4	7.9

Продолжение таблицы 2.17

1	2	3	4
4	6,5-8,0	6,6	11,2
		6.7	7,0
		7.2	8,6
		7.5	9,4
		8,0	10,4

5. Находим среднее значение в каждой группе (таблица 2.18)

Таблица 2.18 – Расчет среднего значения в группе

Группа	Частота	Среднее значение в группе
1	5	3.0
2	8	5,0
3	7	7,3
4	5	9,3

5. Находим общее среднее:

5. Рассчитаем общую дисперсию:

5. Рассчитаем межгрупповую дисперсию:

5. Найдем коэффициент детерминации:

10 Найдем эмпирическое корреляционное отношение:

Таким образом, рассчитанное эмпирическое корреляционное отношение свидетельствует о достаточно высокой статистической связи между x и y.

Контрольные вопросы

1. Дайте понятие статистической связи.

2. Что такое корреляционная зависимость?

3. Приведите примеры корреляционной зависимости.

4. Что такое поле корреляции?

5. Что такое корреляционный момент?

6. Что характеризует корреляционный момент?

7. Для чего служит коэффициент корреляции?

8. Какие может принимать значения коэффициент корреляции?