Контрольные вопросы

7.1. С какими параметрами оптимизации наиболее часто приходится иметь дело при выполнении промышленных и научных экспериментов?

7.2. Каковы основные правила преобразования откликов в безразмерную шкалу со значениями 0 и 1?

7.3. Что обозначает одностороннее и двустороннее ограничение отклика?

7.4. Как выбирается «идеальное» значение отклика?

7.5. Каковы основные правила преобразования откликов в безразмерную шкалу с использованием шкалы желательности?

7.6. Как комбинируются отклики между собой?

7.7. Каковы основные правила преобразования откликов в безразмерную шкалу с использованием «идеального» значения?

7.8. Что такое область определения отклика ?

7.9. С какой целью производится преобразование откликов в безразмерную шкалу?

7.10. Какие шаги необходимо предпринять для построения обобщенного отклика?

7.11. К каким типам шкал относится шкала желательности, между какими параметрами она устанавливает соответствие?

7.12. Как измерить качественные отклики, например вкус блюда?

7.13. Какие способы построения обобщенного показателя существуют? Охарактеризуйте их достоинства и недостатки.

7.14. Что такое параметр оптимизации?

7.15. Когда возникает необходимость построения обобщенного отклика?

7.16. Любой ли отклик может выступать в качестве параметра оптимизации?

Краткие ответы

7.1. При планировании производственных экспериментов, как правило, учитывают экономические параметры оптимизации, такие, как прибыль, себестоимость, рентабельность, затраты прямые и косвенные. Также наиболее часто встречаемые параметры оптимизации в научных и промышленных экспериментах - это качество и количество получаемого продукта. Определенные технические требования к продукту составляют группу технологических параметров оптимизации, например, толщина нити, прочность на растяжение, водонепроницаемость, температура кипения, шероховатость и т.п. Коэффициент полезного действия, надежность, долговечность - примеры технико-экономических показателей.

7.2. При наиболее простом способе преобразования отклика в безразмерную величину, на шкале преобразования будут только два значения - ноль и единица. Неудовлетворительному результату приписывается значение 0, удовлетворительному - (+1).

В зависимости от того, максимальный или минимальный результат будет считаться удовлетворительным, частная функция желательности при одностороннем ограничении будет тгметь вид

= , = .

При двустороннем ограничении, имеющем максимум,

d =

Для построения обобщенного отклика D необходимо взять произведение частных преобразованных откликов:

D = (l=1,2, …,m),

где m - число откликов.

При этом обобщенный отклик будет иметь значение +1 только в том случае, если все частные отклики также равны 1.

7.3. При односторонних ограничениях отклик подчиняется одному из условий: у≥ у_min;„ или у ≤ у_max. К числу свойств, подчиняющихся одностороннему ограничению, относятся очень многие характеристики качества материалов: упругость, прочность, морозостойкость. Как правило, здесь ограничение имеет вид у ≥ _min. Другой вид одностороннего ограничения (у ≤ у_max) характерен для таких показателей, как содержа­ние дорогих или дефицитных компонентов, влажность, концентрация вредных веществ, примесей.

Двустороннее ограничение у_max ≤у ≤ у_min встречается более редко. Примерами могут служить молекулярный вес полимера, насыпной вес, вес утряски, индекс расплава. Индекс расплава, например, является Важной характеристикой литьевых и экструзионных типов полиметилметаакрилата. Слишком низкий индекс наблюдается у материалов с недостаточной текучестью, что отрицательно влияет на ход технологического процесса при переработке полимера. При высоком показателе индекса расплава возникают затруднения во время формования Материала.

7.4. Как правило, значение «идеального» отклика можно определить по технической документации, литературным данным, требованиям технологического процесса с учетом запросов заказчика и, наконец, же­ланий самого исследователя.

Если сведений об идеальном значении у исследователя не имеется, можно за идеальное взять максимальное или минимальное значение отклика в данной серии экспериментов, для параметров оптимизации, стремящихся к максимуму или к минимуму соответственно. Для параметров оптимизации с двусторонним ограничением можно выбрать среднее значение из всех откликов, полученных в данной серии экспериментов.

7.5. Универсальным способом построения обобщенного отклика является метод с использованием шкалы желательности, разработанный Харрингтоном. Готовая разработанная шкала соответствий между отношениями предпочтений и числовыми отметками приведена в табл. 7.1.

Таблица 7.1. Стандартные отметки на шкале желательности

Желательность (значения отклика)	Количественная отметка на шкале
Очень хорошо (отлично)	1,00-0,80
Хорошо	0,80-0,63
Удовлетворительно	0,63-0,37
Плохо	0,37-0,20
Очень плохо	0,20-0,00

Для двустороннего ограничения преобразование измеренного отклика в шкалу d производится при помощи выражения

d = exp [-(|y'|)ⁿ]

где n - положительное число, не обязательно целое, его можно вычислить, если задать некоторому значению у значение d (предпочтительно в интервале от 0,6 до 0,9) по формуле

n = (ln In l/d)/ln|y'|.

Для откликов, имеющих особую важность, величина n должна иметь наибольшее значение. Величину у' можно рассчитать по формуле

y' = [2y – (y_max + y_min)]/( y_max - y_min)

Для односторонних ограничений более удобной формой преобразования у в d служит другая экспоненциальная зависимость:

d = exp[-exp (-у')].

В этом выражении у' = С₀ + C₁y. А коэффициенты С₀ и С₁, можно определить, если задать для двух значений свойства у соответствующие значения желательности d предпочтительно в интервале от 0,2 до 0,8.

Обобщать, т.е. переходить от d к D, предлагается по формуле

D =

Способ задания обобщенной функции желательности таков, что если хотя бы одна частная желательность равна нулю, то обобщенная функция также будет равна нулю. D = 1 тогда и только тогда, когда все d_l = 1.

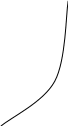
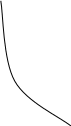
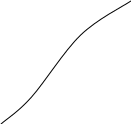
Для перевода откликов в частные функции желательности можно воспользоваться графиками d-y, построенными при различных значениях n (рис. 7.1,7.2).

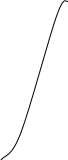
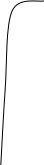
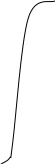
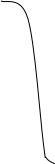
d d

0 ,8 0,8

0,6 0,6

0,4 0,4

0,2 0,2

0 0

-2 -1 0 1 y -2 -1 0 1 y

Рис. 7.1. Функции желательности с Рис. 7.2. Функции желательности с

односторонним ограничением двусторонним ограничением

7.6. Выбор правила комбинирования исходных частных откликов в обобщенный показатель не формализован. Единого правила не существует. Можно, например, комбинировать отклики, учитывающие требования заказчика, и отдельно требования исполнителя или обобщать экономические отклики в один показатель, а эстетические - в другой. При этом не будет ошибкой, если исследователь совсем не желает делить частные отклики по группам, а объединяет их все.

7.7. Если экспериментатору известно наилучшее значение отклика (у^идеал), то разница у_u - у^идеал и будет характеризовать близость к идеалу. Причем чем ближе к нулю, тем результат лучше.

Чтобы нивелировать знаки и размерности у разных откликов, преобразование откликов в безразмерную шкалу проводят по формуле

d =

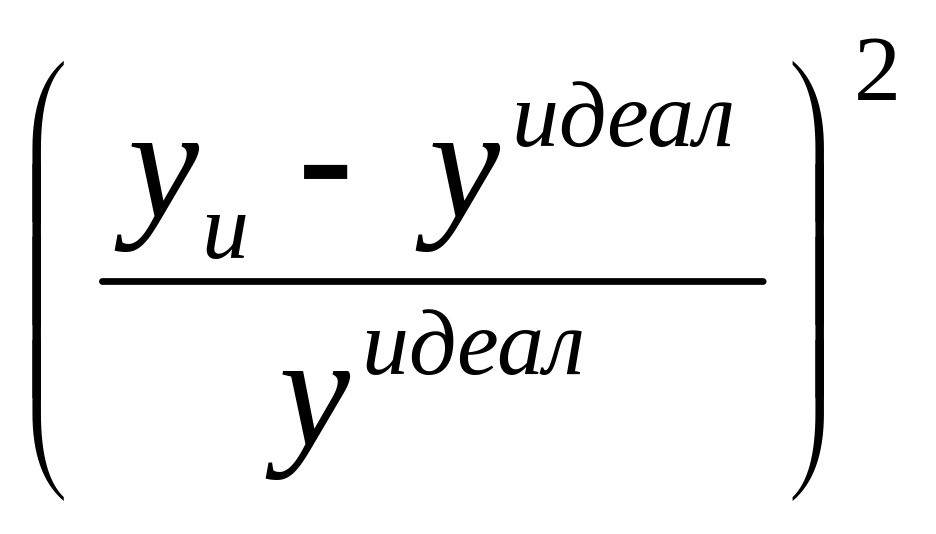
Обобщенный отклик это сумма частных откликов, взятых с учётом их веса:

D_u = ,

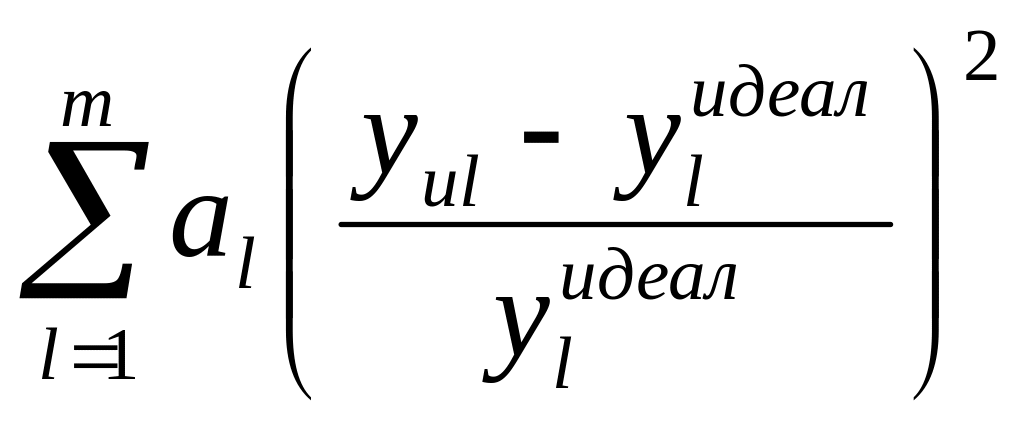здесь а_l вес или важность каждого отклика, причем сумма весов должна быть равна единице.

7.8. Множество значений, которые может принимать параметр оптимизации, называется областью определения. Область определения может быть непрерывной и дискретной. Выход годного продукта, давление в системе - параметры оптимизации с непрерывной областью определения. Количество плодов на одном кусте, число сбоев в работе оборудования - примеры откликов с дискретной областью определения: плохой, хороший, отличный (область определения с тремя значениями).

7.9. Каждый отклик имеет свой физический смысл и свою размерность. Чтобы объединить различные отклики, прежде всего приходится ввести для каждого из них некоторую безразмерную шкалу. Шкала должна быть однотипной для всех объединяемых откликов - это делает юс сравнимыми.

7.10. Любая методика расчета обобщенного отклика предусматривает следующую последовательность действий:

Сначала необходимо ввести для каждого отклика безразмерную шкалу, однотипную для всех объединяемых откликов, что сделает их сравнимыми между собой. Преобразованные частные отклики принято обозначать буквой d.

Затем скомбинировать исходные частные отклики в обобщенный показатель. Обобщенный преобразованный отклик обычно обозначают буквой D.

7 .11. Шкала желательности относится к психофизиологическим шкалам. Ее назначение - установление соответствия между физическими и психологическими параметрами. Здесь под физическими параметрами понимаются всевозможные отклики, характеризующие функционирование исследуемого объекта. Среди них могут быть технические, эстетические, экономические и другие параметры. А под психологическими параметрами понимаются чисто субъективные оценки экспериментатора - желательности (предпочтения) того или иного значения отклика. Шкала желательности имеет интервал от нуля до единицы. Значение d = 0 соответствует абсолютно неприемлемому значению отклика; a d = 1 - самому лучшему значению отклика, причем дальнейшее улучшение его или невозможно, или не представляет интереса. Промежутоные значения желательности и соответствующие им числовые оценки следующие: 0,00 ÷ 0,20; 0,20 ÷ 0,37 - очень плохо; 0,37 ÷ 0,63 - удовлетворительно; 0,63 ÷ 0,80 - хорошо; 0,80 ÷ 1,00 - очень хорошо. Такой выбор числовых отметок объясняется удобством вычислений, поскольку d = 0,63≈l-l/e, a d = 0,37 ≈ l/e.

7.12. Экспериментатор должен иметь возможность измерить отклик при всех выбранных комбинациях факторов. Часто для получения количественных характеристик отклика нет возможности для его непосредственного измерения. С такой ситуацией приходится сталкиваться для оценки эстетических или органолептических показателей, например, при сравнении произведений искусства, дегустации, конкурсном отборе претендентов. Для получения количественных оценок качественных откликов можно привлечь группу экспертов и воспользоваться методами ранжирования откликов (см. практ. занятие 1).

7.13. К простейшим способам построения обобщенного отклика можно отнести способ преобразования откликов в безразмерную шкалу с двумя значениями 0 и 1 и способ преобразования с использованием идеального значения. Совершенно очевидно, что первый подход слишком груб и не гибок. Он не позволяет рассчитать уравнение регрессии, этот подход к построению обобщенного отклика годится только для получения предварительной информации о системе. Второй метод прост в исполнении, дает возможность выявить наиболее существенные факторы, рассчитав уравнение регрессии, но требует введения субъективной характеристики - веса фактора.

Одним из наиболее удачных способов решения задачи оптимизации процессов с большим количеством откликов является использование предложенной Харринтоном в качестве обобщенного критерия оптимизации так называемой обобщенной функции желательности D. Однако, в отличие от первых двух методик, расчет обобщенного показателя требует большого объема математических выкладок.

7.14. Параметр оптимизации - это реакция (отклик) системы на воздействие факторов. Причем эта реакция может быть многообразна, и задача исследователя четко определить, какой именно отклик наиболее полно отражает поведение системы. Характеристика цели, заданная количественно, и есть параметр оптимизации.

7.15. Если исследователя интересует только один из возможных откликов системы, то остальные могут служить просто ограничениями. Если система характеризуется многими откликами, причем не удается выделить один - самый важный, возникает необходимость объединить отклики в единый показатель.

7.16. Чтобы отклик мог выступать в роли параметра оптимизации, он должен удовлетворять ряду требований: быть количественным, выражаться одним числом, быть однозначным. Рассмотрим эти требования более подробно. Параметр оптимизации должен быть однозначен, т.е. заданному набору значений факторов должно соответствовать только одно значение (с точностью до ошибки эксперимента) параметра оптимизации. При этом необходимо, чтобы значение отклика выражалось одним числом. Например, соотношение бракованных и годных изделий необходимо брать в виде числа 20 %, а не 1:5 . Желательно, чтобы параметр оптимизации был простым, легко вычисляемым и имел физический смысл.