Контрольные вопросы

3.1 Какова методика разбиения матрицы эксперимента на четыре блока?

3.2 От чего зависит точность результатов измерения?

3.3 Как можно доказать, что измерение является грубым?

3.4 Какие матрицы и на какие блоки можно разбить?

3.5 Совпадают ли понятия точности и правильности измерений?

3.6 Какими способами можно уменьшить влияние систематических ошибок на результат исследования?

3.7 В каких случаях применяется разбиение матрицы на блоки?

3.8 Чем отличаются систематические и случайные ошибки?

3.9 Для чего нужна таблица случайных чисел при составлении плана эксперимента?

3.10 Какова методика разбиения матрицы эксперимента на два блока?

3.11Как рандомизировать условия проведения опытов по табли­це случайных чисел?

3.12 Для чего нужна рандомизация опытов? Что обозначает дан­ный термин?

Краткие ответы

3.1. Чтобы произвести разбиение матрицы на четыре блока, число взаимодействий, которыми можно будет пренебречь, должно быть равно трем. Два таких взаимодействия можно выбрать произвольно, а третье однозначно определяется по следующему правилу: нужно взять алгебраическое произведение первых двух выбранных взаимодействий и заменить единицей каждый множитель, стоящий в квадрате.

Пусть нужно поставить эксперимент . Заведомо известно, что имеется четыре источника неоднородности, например, четыре партии сырья, которые могут значительно исказить результаты эксперимента. Задача состоит в том, чтобы в уравнении регрессии линейные эффекты были освобождены от влияния межблокового эффекта, однако при разбиении матрицы на четыре блока одно из парных взаимодействий окажется неизбежно смешанным с межблоковым эффектом. Так, если двумя произвольно выбранными взаимодействиями являются парные и , то третьим будет . Если выбранными являются тройные и , то третьим будет :

Три взаимодействия: и оказались выбранными для смешивания. При разбиении матрицы на блоки необходимо выбрать строки, имеющие идентичные для этих взаимодействий уровни. Тогда матрица планирования эксперимента приобретает вид, представленный в табл. 3.1.

Таблица 3.1. Разбиение матрицы 24 на четыре блока

Блок	Буквенное обозначение
I	(-1)	-1	-1	-1	-1	-1	-1	+1
	bc	-1	+1	+1	-1	-1	-1	+1
	acd	+1	-1	+1	+1	-1	-1	-1
	abd	+1	+1	-1	+1	-1	-1	-1
II	а	+1	-1	-1	-1		-1	-1
	abc	+1	+1	+1	-1	+1	-1	-1
	cd	-1	-1	+1	+1	+1	-I	+1
	bd	-1	+1	-1	+1	+1	-1	+1
III	b	-1	+1	-1	-1	+1	+1	-1
	с	-1	-1	+ 1	-1	+1	+1	-1
	abcd	+1	+1	+1	+1	+1	+1	+1
	ad	+1	-1	-1	+1	+1	+1	+1
IY	d	-1	-1	-1	+1	-1	+1	-1
	bcd	-1	+1	+1		-1	+1	-1
	ac	+1	-1	+1	-1	-1	+1	+1
	ab	+1	+1	-1	-1	-1	+1	+1

3.2.Результаты экспериментов содержат погрешности – ошибки, которые возникают, в частности, вследствие того, что условия измерений в течение физического процесса измерения могут меняться.

Абсолютной погрешностью (ошибкой) измерения s называется разность между результатом измерения у и действительным значением Y измеряемой величины:

ε = у - Y.

Относительной погрешностью (ошибкой) измерения δ называется отношение (в том числе процентное) абсолютной ошибки ε к результату измерения у:

δ = ε / у.

Ошибки измерения можно классифицировать на пять (условных в силу взаимозаменяемости понятий в конкретной измерительной ситуации) групп.

1. Ошибки, вызванные объектом исследования: изменением объекта во времени (старение материала, разложение катализатора, увеличение возраста или уровня знаний в исследуемой социальной группе и т.п.); неоднородностью объекта в пространстве (влияние структурной неоднородности в месте контакта измерительного датчика, переход от образца к образцу при разрушающем контроле и т. д.); влиянием процесса измерения на состояние объекта (ряд измерений в атомной физике и микромире, биофизические измерения с вживленными датчиками, изме­нение поведения и ответов на вопросы в исследуемой социальной группе под влиянием психического напряжения или целевой установки и т.п.).

2. Ошибки оператора, связанные с уровнем его квалификации (обучение, опытность, сознание ответственности и т.п.) и психофизиологическим состоянием (усталость - болезнь, возбуждение - торможение; реакция на шумы и другие внешние раздражители и т.п.).

3. Инструментальные, ошибки, связанные с погрешностями измерительных приборов и испытательных машин.

4. Методические ошибки, связанные, с одной стороны, с неправильными или упрощенными представлениями о закономерностях проявления некоторого свойства объекта (или о закономерностях взаимодействия объекта с измерительным комплексом), а с другой, - со степе­нью разработки методики проведения измерительных операций (отбор образцов, порядок операций, обоснованность допусков, полнота учета факторов и ограничений на них и т.д.).

5. Ошибки, обусловленные влиянием внешней среды (температура, загазованность и т.п.) на исследуемый объект и измерительную систему.

Качество исследования определяется тем, насколько экспериментатору удается устранить (или компенсировать) воздействие вышеуказанных источников ошибок на результат измерения.

3.3. Важно исключить из ряда экспериментальных данных аномальные (грубые ошибки, «промахи», так называемый брак при повторных опытах), если они допущены. Поскольку даже опытному экспериментатору трудно только на логическом уровне решить вопрос об аномальности того или иного результата, то следует использовать статистические критерии для проверки такой гипотезы.

Проверка при малом числе наблюдений может быть осуществлена согласно критерию Романовского. Результат (r + 1)-го сомнительного опыта исключается и по остальным r опытам находится среднее и дисперсия:

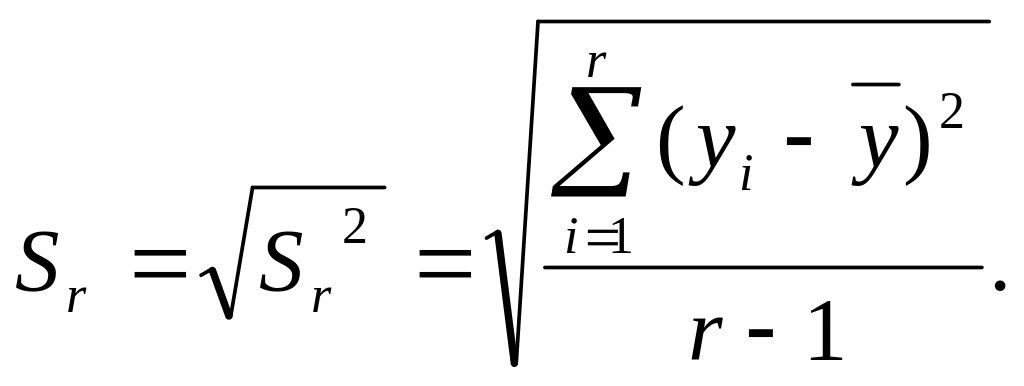
Результат (г + 1)-го сомнительного опыта отбрасывается, если

Значения критерия Стьюдента при различных доверительных интервалах и степенях свободы приведены в прил. 1.

Можно воспользоваться критерием. Если имеется выборка , и - наибольший (наименьший) результат измерения, то величина должна быть исключена из выборки как грубое измерение, если для нее больше табличного (см. прил. 4):

; .

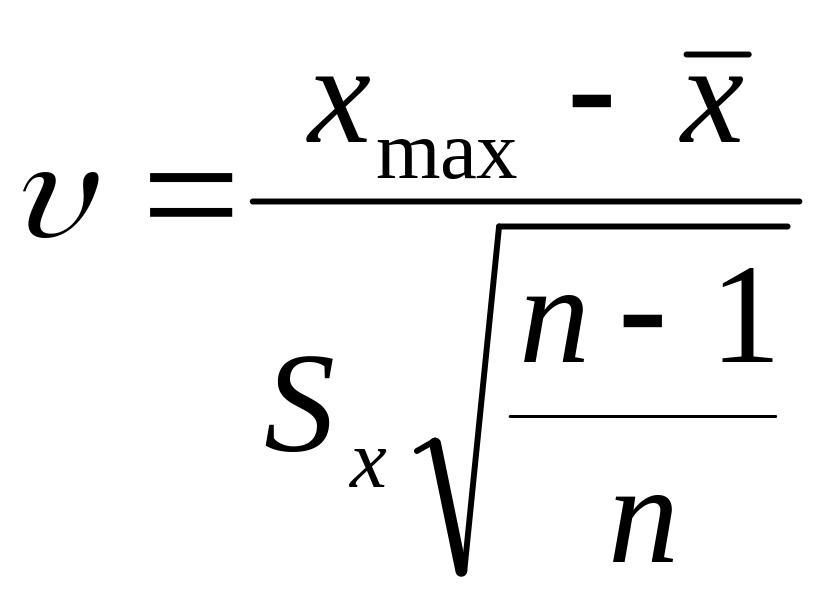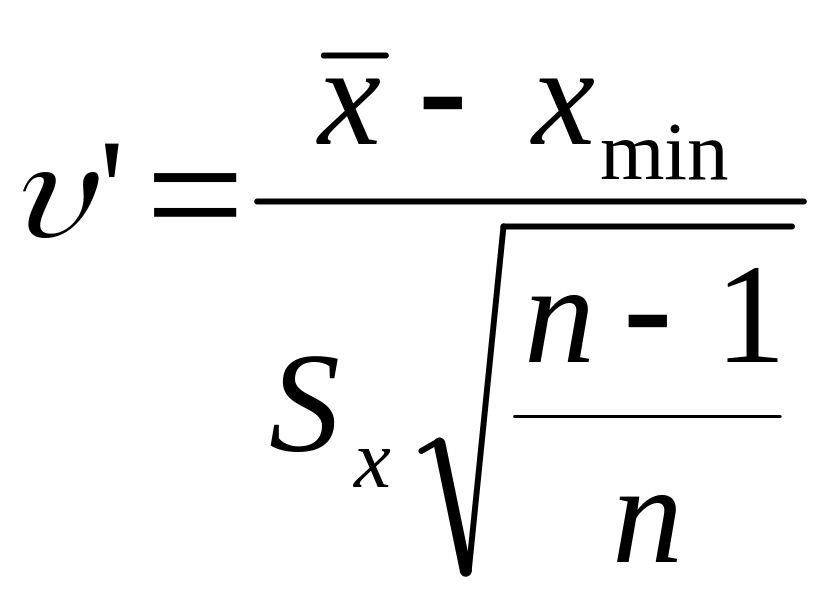3.4 Матрицу типа можно разбить на количество блоков при n < к (n - степень двойки). Так, матрица разбивается на два блока по четыре опыта в каждом и на четыре блока по два опыта в каждом. Матрица - на два блока по восемь опытов в каждом, на четыре блока по четыре опыта и на восемь блоков по два опыта и т. д.

3.5 Необходимо различать понятия правильности и точности результатов измерения. Правильность измерения характеризуется систематической ошибкой, а точность - оценкой среднеквадратического отклонения S, характеризующего случайную ошибку.

3.6 Способом включения систематических ошибок в число случайных является рандомизация. Рандомизация позволяет уменьшить систематическую ошибку, если источник ее предсказать трудно. Если источник неоднородности известен, то можно воспользоваться методом разбиения матрицы на блоки.

3.7 Если источники систематических ошибок известны заранее (например, количество партий сырья, количество аппаратов), то целесообразно разбить матрицу планирования эксперимента на блоки. Межблоковый эффект при этом смешивается с взаимодействием, которым экспериментатор может пренебречь.

3.8 Грань между случайными и систематическими ошибками провести достаточно сложно, так как последние могут в соответствующих условиях рассматриваться как случайные величины. Способом включения систематических ошибок в число случайных является рандомизация.

Погрешность измерения можно условно разделить на две части: систематическую h и случайную .

Систематическими ошибками h можно назвать такие ошибки, величина которых во всех измерениях, проводящихся одним и тем же методом с помощью одних и тех же приборов, одинакова или изменяется по некоторому закону в зависимости от источников возникновения ошибок.

Случайными ошибками , можно назвать такие ошибки, величина которых во всех измерениях, проводящихся одним и тем же методом и с помощью одних и тех же приборов, изменяется. Случайные ошибки независимых измерений подчиняются нормальному закону распределения, что и определяет их свойства.

3.9. Если источник систематических ошибок не известен, то для рандомизации удобно пользоваться случайными числами. Порядок выполнения опытов может быть намечен по таблице случайных чисел (см. прил. 5), или с использованием вычислительной техники, способной генерировать случайные числа.

3.10. Для разбиения любого эксперимента типа 2к на два блока следует выбрать взаимодействие, которым можно пожертвовать (чаще это взаимодействие самого высокого порядка). Взаимодействием низкого порядка, например двойным, можно пожертвовать в том случае, если известно, что оно лишено физико-химического смысла. Далее в первый блок необходимо сгруппировать все опыты, в которых это взаимодействие равно +1, а во второй, где оно равно -1.

Например, если планируется проводить эксперимент одновременно на двух идентичных установках, то матрицу полного факторного эксперимента для трех факторов на двух уровнях (из восьми опытов) можно разбить на два блока (табл. 3.2), так, чтобы эффект от возможного влияния разницы установок отразился только на величине трехфакторного взаимодействия . При составлении первого блока (планировании опытов, проводимых на первом станке) необходимо сгруппировать все строки, для которых , на втором станке проводить опыты, для которых этот эффект равен -1.

Таблица 3.2. Разбиение матрицы на два блока

Блок								y
I	-1	-1	+1	+1	-1	-1	+1
	+1	-1	-1	-1	-1	+1	+1
	-1	+1	-1	-1	+1	-1	+1
	+1	+1	+1	+1	+1	+1	+1
II	-1	-1	-1	+1	+1	+1	-1
	+1	-1	+1	-1	+1	-1	-1
	-1	+1	+1	-1	-1	+1	-1
	+1	+1	-1	+1	-1	-1	-I

Система смешивания эффектов при таком разбиении будет иметь вид

= 1/8 [( ) + ( ) + ( ) + ( ) + + + + ];

= 1/8 [-( ) + ( ) -( ) + ( ) - + - + ];

Аналогичные расчеты для остальных коэффициентов показывают, что они не смешаны друг с другом и остальными эффектами взаимодействия:

.

Эффект смены оборудования может отразиться только на взаимодействии второго порядка :

=1/8 [( )+( )+( ) + ( ) - - - - ],

Межблоковый эффект отразится на подсчете и . Остальные коэффициенты регрессии освобождены от влияния источников неоднородности.

3.11. Если, например, необходимо провести восемь опытов, то, согласно фрагменту случайных чисел (см. прил. 5), получаем следующую последовательность опытов:

7,2,4, 8,3,5,1,6 - при движении по строкам таблицы слева направо;

4,1,2,7,3,6,8,5 - при движении по столбцам таблицы сверху вниз.

Выбранную случайным образом последовательность опытов не рекомендуется нарушать.

Данная методика оправдывает себя в тех случаях, когда источник систематических ошибок заранее предсказать трудно.

3.12. Для компенсации влияния систематических ошибок опыты рандомизируются во времени. Термин рандомизация происходит от английского слова random - случайный. Таким образом, рандомизировать - значит провести опыты в случайном порядке.

Если источник систематических ошибок не известен, то для рандомизации удобно пользоваться случайными числами. Порядок выполнения опытов может быть намечен по таблице случайных чисел или с использованием вычислительной техники, способной генерировать случайные числа.

Если источники систематических ошибок известны заранее (например, количество партий сырья, количество аппаратов), то целесообразно разбить матрицу планирования эксперимента на блоки. Межблоковый эффект при этом смешивается с взаимодействием, которым экспериментатор может пренебречь.