Контрольные вопросы

1.1. Что представляют собой полиномы разных степеней?

1.2. Как определить степень согласованности в работе экспертов?

1.3. Как построить диаграмму рангов?

1.4. Какая модель является адекватной эксперименту?

1.5. Что такое фактор? Какими свойствами обладают факторы?

1.6. Зачем рассчитывают коэффициент конкордации? Как оценить его значимость?

1.7. Что такое априорное ранжирование факторов? Как на практике осуществить априорное ранжирование факторов?

1.8. С чего начать эксперимент, если факторов, влияющих на объект исследования много?

1.9. Что представляет собой модель исследования?

1.10. Каковы требования к совокупности фактов?

1.11. Как выделить наиболее существенные факторы?

1.12. Как узнать, сколько коэффициентов будет в полиноминальной модели?

1.13. Что такое эксперимент? Чем различаются активные и пассивные эксперименты?

1.14. Какие факторы могут быть включены в активный эксперимент?

1.15. Каковы критерии выбора модели исследования?

1.16. На чем основано сравнение объекта исследования с «черным ящиком»?

1.17. Как интерпретировать априорную диаграмму рангов?

Краткие ответы

1. Полином - это частный случай регрессионной модели, когда функции факторов 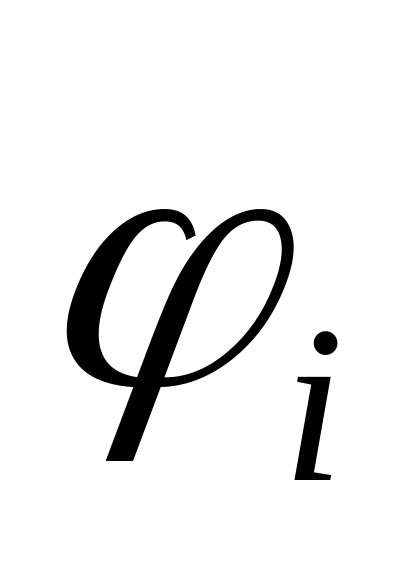являются степенными. Общий вид полинома степени d от k факторов представлен ниже:

здесь где - выборочные коэффициенты регрессии, которые можно получить, пользуясь результатами эксперимента.

Полиномы различаются по максимальным степеням входящих в них переменных. Для двух факторов полиномы будут иметь следующий вид:

нулевой степени: ;

первой степени: ;

второй степени: ;

третьей степени: + .

1.2 Степень согласованности мнений специалистов оценивается по коэффициенту конкордации – W. Для расчета W подсчитывается сумма рангов каждого фактора, средняя сумма рангов , разность между суммой рангов каждого фактора и средней суммой рангов их квадраты , а также сумма квадратов этих разностей S:

.

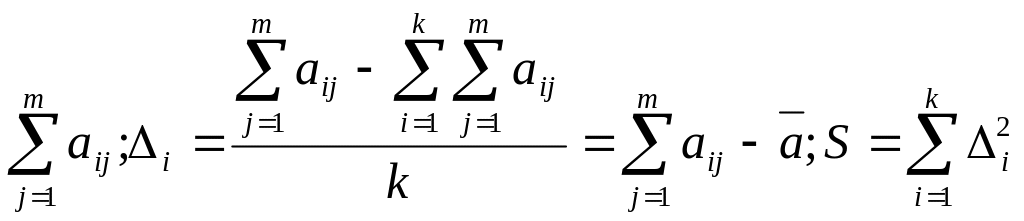Для проверки значимости самого коэффициента конкордации можно воспользоваться критерием (значения приведены в прил. 3).

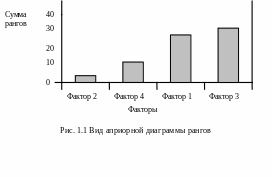
1.3 На априорной диаграмме рангов (рис. 1.1) по оси абсцисс откладываются факторы, а по оси ординат – соответствующие суммы рангов. Факторы должны следовать в порядке увеличения их суммы рангов. По оси ординат можно также откладывать и средние значения рангов для факторов, что повлияет лишь на масштаб диаграммы вдоль оси ординат.

1.4 Проверка адекватности – строго формализованная статистическая процедура, выполняемая с помощью F – критерия Фишера:

где - дисперсия адекватности; - дисперсия, характеризующая ошибку опыта.

Модель считается адекватной в том случае, если расчетное значение критерия F, не превышает соответствующего табличного, при некотором уровне значимости. Обычно при решении инженерных задач уровень значимости принимается равным 0,05 (5 %).

1.5. Фактором называется измеряемая переменная величина, принимающая в некоторый момент времени определенное значение. Факторы соответствуют способам воздействия на объект исследования.

Каждый фактор имеет область определения, т.е. совокупность всех значений, которые в принципе может принимать данный фактор. В практических задачах области определения факторов, как правило, ограничены. Ограничения могут носить принципиальный либо технический характер. Совокупность значений фактора, которая используется в эксперименте, является подмножеством из множества значений, образующих область определения. Область определения может быть непрерывной и дискретной. Однако для факторов с непрерывной областью определения, таких, как температура, время, количество вещества, всегда выбираются дискретные множества уровней.

Факторы подразделяются на количественные и качественные. Качественные факторы - это разные вещества, разные технологические способы, аппараты, исполнители и т.д. Время реакции, температура, концентрация реагирующих веществ, скорость подачи веществ, величина pH - это примеры наиболее часто встречающихся количественных факторов. В ряде случаев граница между понятием качественного и количественного фактора весьма условна.

1.6. Коэффициент конкордации может меняться от 0 до 1, что означает либо полное несогласие, либо полное согласие во мнениях опрошенных. Гипотеза о наличии согласия между исследователями не отвергается, если расчетное значение - критерия больше табличного (см. прил. 3) при выбранном уровне значимости и числе степеней свободы f = к- 1:

1.7. Априорное ранжирование - эхо психологический эксперимент, основанный на методах ранговой корреляции. Проранжировать - значит расставить объекты экспертизы в порядке возрастания или убывания, т. е. присвоить им ранг.

Так как мнение одного специалиста носит субъективный характер, для объективной оценки информации о процессе целесообразно учитывать мнения многих специалистов. При этом каждый специалист должен расположить исследуемые факторы в порядке убывания их воздействия на параметр оптимизации - проранжировать. Ранг i-го фактора у j-го исследователя - может принимать одно из значений множества {1,2, ...,к}.

1.8. Включение в программу исследования всех «подозреваемых» факторов может потребовать значительного увеличения экспериментальных работ. Детальное исследование всех переменных оказывается практически невозможным из-за большого числа опытов, поэтому появляется необходимость предварительного отсеивания факторов, оказывающих меньшее влияние, и выделения наиболее существенных факторов для их дальнейшего детального изучения.

1.9. Зависимость между выходным параметром (откликом) и входными параметрами (факторами) называется функцией отклика и имеет следующий вид:

у = где у - отклик (результат эксперимента); - независимые переменные (факторы), которые можно варьировать при постановке экспериментов.

Полученное эмпирическим путем уравнение, связывающее отклики и факторы, часто называют математической моделью (или просто моделью) процесса. Некоторая гиперповерхность в многомерном пространстве соответствующая данному уравнению, называется поверхностью отклика, а пространство, в котором существует указанная поверхность, - факторным пространством. В простейшем случае, когда исследуется зависимость отклика от одного фактора, поверхность отклика представляет собой линию на плоскости, т.е. в двухмерном пространстве. В общем случае, когда рассматриваются k факторов, уравнение описывает поверхность отклика в (k+1)-мерном пространстве.

Модель называют регрессионной, если она имеет вид

где - известные функции k факторов, а - неизвестные коэффициенты (эффекты), которые исследователь должен оценить по результатам наблюдений.

В регрессионную модель эффекты должны входить обязательно линейно. Например, модель - регрессионная, а модель таковой не является.

Частным случаем регрессионной модели является полином. При весьма ограниченных знаниях о механизме процесса аналитическое выражение функции отклика неизвестно. Поэтому и приходится ограничиваться представлением ее полиномом.

1.10. При планировании эксперимента обычно одновременно изменяется несколько факторов, поэтому очень важно сформулировать требования, которые предъявляются к совокупности факторов. Прежде всего выдвигается требование совместимости. Совместимость факторов означает, что все их комбинации осуществимы и безопасны.

При планировании эксперимента важна независимость факторов, т.е. возможность установления фактора на любом уровне вне зависимости от уровней других факторов.

1.11. Если число факторов велико, нужно обратиться к методам отсеивания несущественных факторов. Здесь можно воспользоваться формализацией априорной информации, методом случайного баланса, планами Плаккета-Бермана и др. Существуют и экспериментально-статистические методы отсеивания.

1.12. Число эффектов в полиноминальной модели порядка d для k факторов можно рассчитать по формуле

1.13. Для получения выборочных оценок коэффициентов регрессии можно организовать проведение эксперимента двумя принципиально различными путями. Первый, более простой путь состоит в том, что исследователь дает возможность некоторым условиям, в которых протекает процесс, произвольным образом изменяться, фиксируя эти условия и соответствующий им результат. Эксперимент, организованный таким образом, обычно называют пассивным. Пассивный эксперимент не нашел широкого применения для математического описания, оптимального управления и оптимизации систем.

Второй путь состоит в том, что экспериментатор изменяет условия по специально разработанной программе и фиксирует только те результаты, которые получены при этих заранее предусмотренных условиях. Эксперимент, организованный по второй схеме, называется активным. Планирование эксперимента базируется преимущественно на активном эксперименте.

1.14. В план эксперимента можно включать только управляемые факторы, т.е. экспериментатор должен иметь возможность, выбрав нужное значение фактора, поддерживать его постоянным в течение всего опыта. В этом состоит особенность «активного» эксперимента. Температура нагрева колбы - управляемый фактор, а температурой воздуха на открытой площадке управлять невозможно. Ее можно только контролировать.

Точность замера факторов должна быть возможно более высокой. Степень точности определяется диапазоном изменения факторов. При изучении процесса, который длится десятки часов, нет необходимости учитывать доли минуты, а в быстрых процессах, возможно, необходимо учитывать, доли секунды. Если факторы измеряются с большой ошибкой или особенность объекта исследования такова, что значения факторов трудно поддерживать на выбранном уровне (уровень фактора «плывет»), то экспериментатору следует обратиться к конфлюэнтному анализу.

Факторы должны непосредственно воздействовать на объект. Они должны быть однозначными, т.е. не являться функцией других факторов. Но в планировании могут участвовать сложные факторы, такие, как соотношения между компонентами, их логарифмы и т.п.

1.15. Главное требование к модели - это способность предсказывать направление дальнейших опытов, причем с требуемой точностью. Это значит, что в некоторой подобласти, в которую входят и координаты выполненных опытов, предсказанное с помощью модели значение отклика не должно отличаться от фактического больше, чем на некоторую заранее заданную величину. Модель, которая удовлетворяет такому или какому-либо аналогичному требованию, называется адекватной. Проверка выполнимости этого требования называется проверкой адекватности модели. Если несколько различных моделей отвечают нужным требованиям, то следует предпочесть ту из них, которая является самой простой. Наиболее простой путь - это представление функции отклика полиномом. На начальном этапе исследований ограничиваются линейной моделью, затем постепенно повышают степень полинома до тех пор, пока модель не окажется адекватной.

Эксперимент нужен только для того, чтобы найти численные значения коэффициентов полинома. Поэтому чем больше коэффициентов, тем больше опытов окажется необходимым. Чем ниже степень полинома при заданном числе факторов, тем меньше в нем коэффициентов. Надо найти такой полином, который содержит как можно меньше коэффициентов, но удовлетворяет требованиям, предъявленным к модели, т.е. оптимальная полиноминальная модель содержит минимум коэффициентов, но адекватно описывает эксперимент.

1.16. Зачастую, приступая к решению экспериментальных задач, исследователь не имеет исчерпывающих сведений о механизме процесса. Он может только назвать параметры, определяющие условия протекания процесса, и требования к его результатам. Ответ на вопрос о природе данного явления остается «за кадром», т.е. сам объект исследования представляет из себя «черный ящик», информация об элементарных операциях внутри которого чрезвычайно мала (рис. 1.2). Стрелками, входящими в объект, показаны входные параметры, которые могут быть управляемыми (х) и неуправляемыми ( ). Работа объекта может характеризоваться несколькими выходными параметрами (у), которые на схеме обозначены стрелками, выходящими из прямоугольника.

Рис. 1.2. Схема «черного ящика»

1.17. Если распределение факторов по рангам близко к равномерному или наблюдается слабое монотонное возрастание, то отдать предпочтение каким-либо факторам трудно (либо сильно влияние всех этих факторов, либо низок уровень априорной информации), поэтому желательно включить все факторы в реальный физический эксперимент.

Если распределение неравномерное, возрастание быстрое, то можно отбросить часть факторов с наибольшей суммой рангов (шумовое поле). Если на диаграмме имеются ярко выраженные скачки, то в эксперимент желательно включить все факторы до скачка.