2.2.Системы координат, применяемые в геодезии и картографии

При производстве топографо-геодезических работ используют географическую (астрономическую), плоскую прямоугольную, полярную, геодезическую и зональную системы координат и высот.

2.2.1.Географическая (астрономическая) система координат

Положение любой точки М, лежащей на поверхности земного шара – геоида (рис. 2 .2), определяется ее географической широтой φ и географической долготой λ, которые получают из астрономических наблюдений.

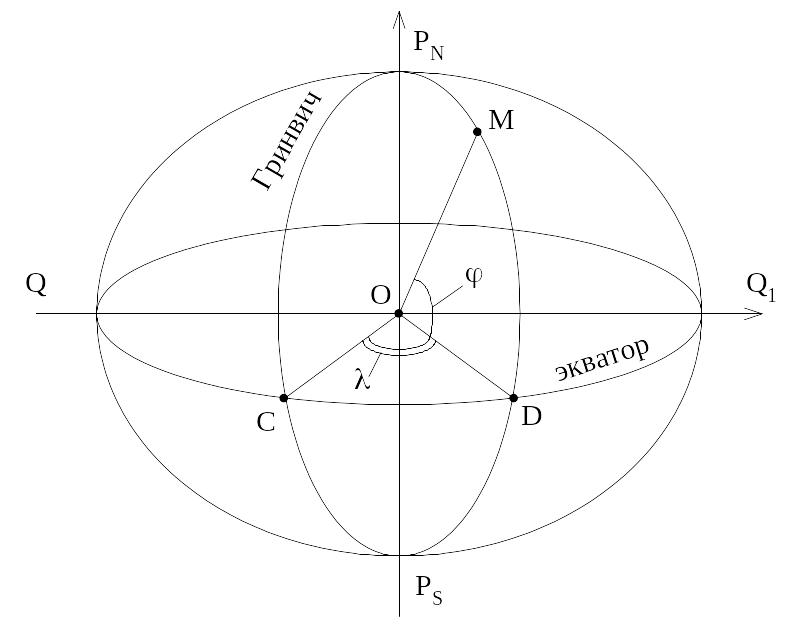
Рис. 2.2. Схема определения положения точки в географической системе координат

На рис. 2 .2 P_N, P_S – обозначение точек полюсов, соответственно северного и южного, а QQ₁ – линия экватора.

При этом координаты φ, λ точки М определяются следующим образом. Пусть МО – отвесная линия (нормаль к уровню поверхности геоида); φ – угол между отвесной линией и плоскостью экватора (на север берется со знаком «+», на юг – со знаком «–»); λ – двугранный угол между меридианом данной точки М и начальным (Гринвичским) меридианом. Счет долготы ведется от Гринвича на 180 на запад со знаком «–», а на восток – со знаком «+».

2.2.2.Геодезическая система координат

Положение любой точки А на поверхности эллипсоида определяется геодезической широтой B и долготой L, которые определяют по результатам геодезических измерений (рис. 2 .3). При этом L – это угол между Гринвичским меридианом и меридианом, проходящим через точку A, а B – угол между нормалью к поверхности эллипсоида в данной точке и плоскостью экватора.

Заметим, что в географической (астрономической) и геодезической системах координат используются разные модели Земли: в первой – геоид, во второй – эллипсоид.

Взаимное расположение отвесных линий и нормалей к поверхности эллипсоида и геоида приведено на рис. 2 .4.

Рис. 2.3. Схема определения положения точки в геодезической системе координат

Рис. 2.4. Схема расположения отвесной лини к поверхности геоида и нормали к поверхности референц-эллипсоида

E – уклонение отвесной линии от нормали, обычно Е3-4, в отдельных регионах до десятков секунд. Учтем, что 1  31 м на поверхности Земли. Следовательно, координаты одной и той же точки в географической и геодезической системах координат могут различаться на 100 м и более.

2.2.3.Система прямоугольных координат

Схема использования прямоугольных координат изображена на рис. 2 .5.

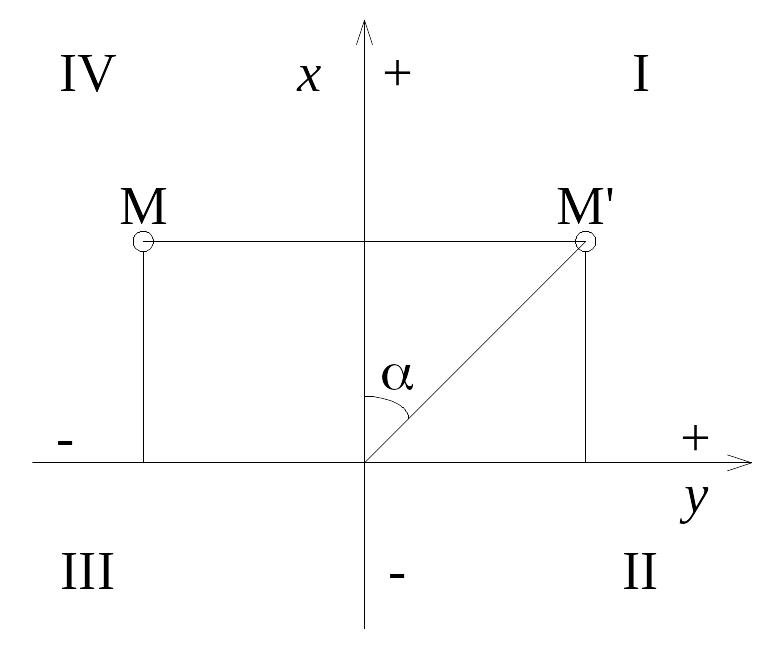
Рис. 2.5. Положение точек M и M' в системе прямоугольных координат

Углы отсчитываются от положительного направления оси х по ходу часовой стрелки. Положение любой точки М в этой системе определяется координатами х и у с соответствующими знаками.

2.2.4.Полярная система координат

Схема полярной системы координат изображена на рис. 2 .6., где

О – полюс,

ОХ – полярная ось (меридиан),

d – расстояние до объекта.

Положение любого пункта можно определить по радиусу r(d) и углу  между полярной осью (ось OX) и направлением на координируемый объект.

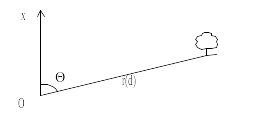
Рис. 2.6. Система полярных координат

2.2.5.Зональная система координат

Зональная система координат используется для определения прямоугольных координат в проекции Гаусса-Крюгера. Поверхность Земли разбивается на 60 зон, каждая по 6^о шириной. Так как абсциссы х отсчитываются от экватора к полюсам, то для территории России, расположенной в северном полушарии, они будут всегда положительные. Ординаты же в каждой зоне будут как положительными, так и отрицательными, в зависимости от того, где находится точка по отношению к осевому меридиану каждой зоны (на запад «–» ; на восток «+»).

Для удобства в работе необходимо избавиться от отрицательных значений ординат в пределах каждой зоны. Расстояние от осевого меридиана зоны до ее крайнего меридиана даже в самом широком месте зоны 330 км. Но для расчетов удобнее взять расстояние, равное круглому числу километров. С этой целью, ординату осевого меридиана зоны условились считать равной 500 км. За начало координат для каждой зоны принимают точку с координатами х=0 км, у=500 км (рис. 2 .7). Так как одинаковые координаты точек могут повториться в каждой из 60 зон, необходимо указывать номер зоны, в которой расположен данный пункт (при указании координаты у).

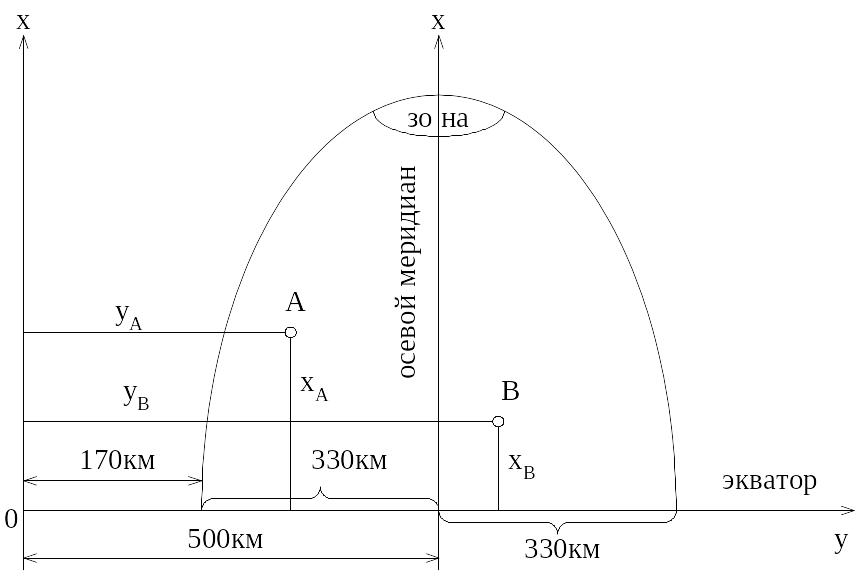
Рис. 2.7. Зональная система координат

Пример записи координат точек A и B для 7-й зоны:

х_А = 6136000 м, х_В = 4200000 м.

у_А = 7316000 м, у_В = 7630000 м.