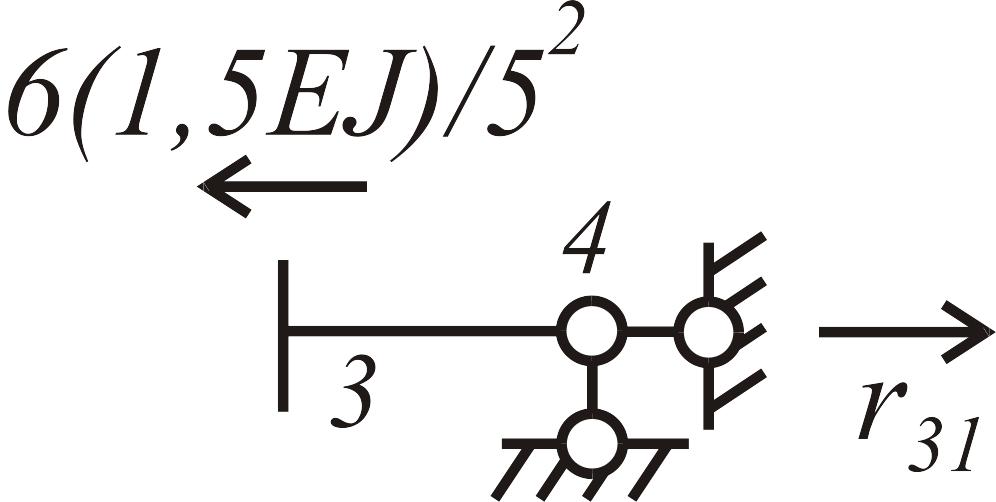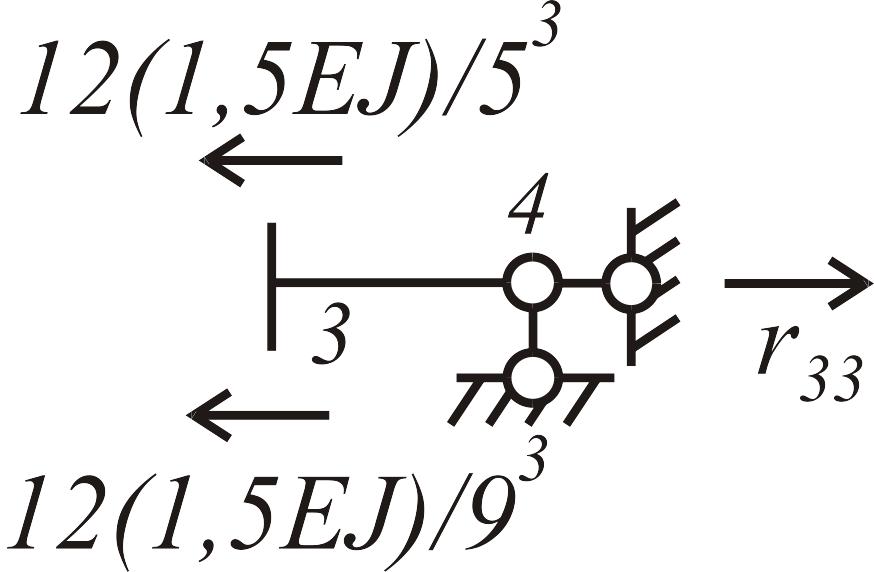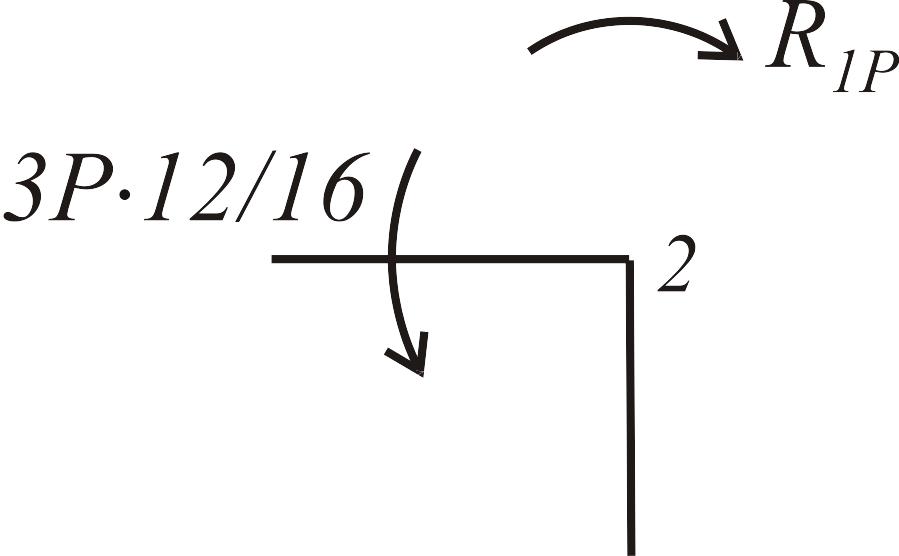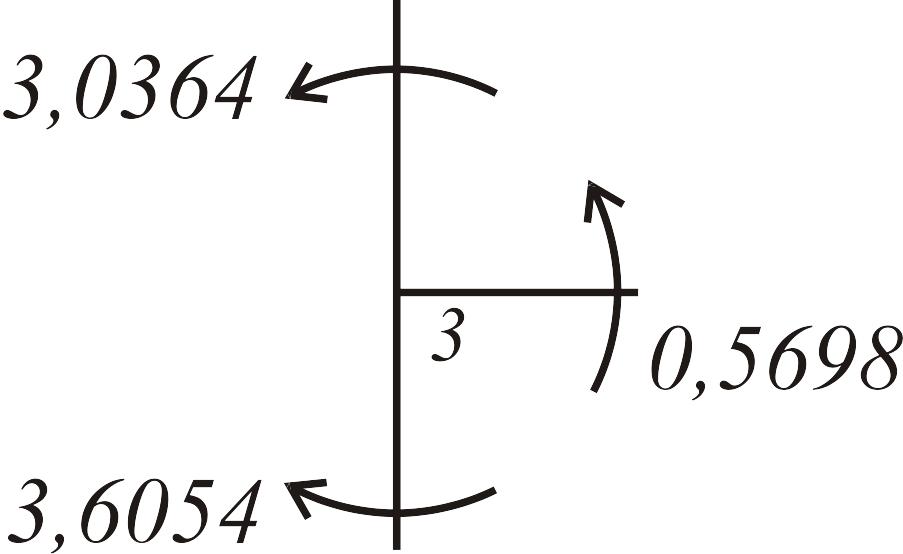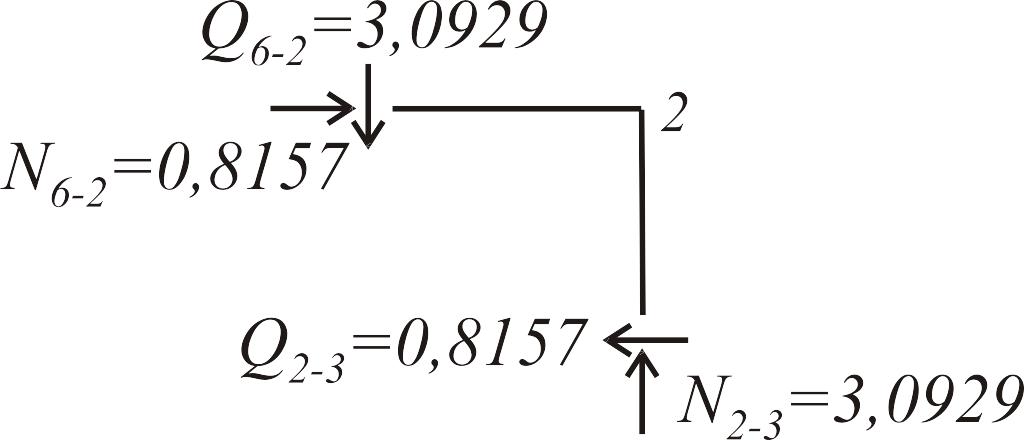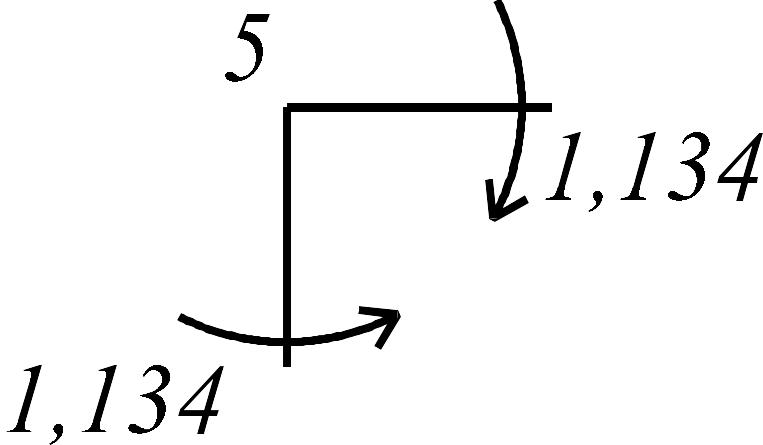Окончание табл. 5
Схема |
Уравнения равновесия |
Величина коэффициента |
Состояние 1 (эпюра )
|
:
|
|
Состояние 2 (эпюра )
|
:
|
|
Состояние 3 (эпюра )
|
:
|
|
Грузовое состояние (эпюра )
|
|
|
Грузовое состояние (эпюра )
|
:
|
|
Грузовое состояние (эпюра )
|
:
|
|
:
Подставим значения коэффициентов в систему уравнений:
Решим систему уравнений, используя ПЭВМ:
;
;
.
Проверим правильность решения, подставив его значения в систему уравнений:
Действительную (окончательную) эпюру строим сложением грузовой эпюры (рис. 3.16 г) и исправленных эпюр (рис. 3.17 а-в).
а |
|
б |
|
в |
|
г |
|
Рис.3.17
Выполним статическую проверку окончательной эпюры моментов . Для этого вырежем узлы 2, 3 (рис. 3.18 а, б) и рассмотрим их равновесие.
а |
|
б |
|
Рис. 3.18
Рис. 3.19
от силы
в выбранной по методу сил основной
системе (рис. 3.19). «Умножив» ее на
окончательную эпюру
,
определим перемещение по направлению
:
.
Погрешность
равна
.
Построим
эпюры
и
.
Определим поперечные силы, используя
дифференциальные зависимости
от
:
.
Тогда
|
|
|
|
|
|
;
;
;
;
.
Продольные силы найдем по известным величинам поперечных сил, исходя из условий равновесия узлов рамы (рис. 3.20 а, б).
а |
|
б |
|
Рис. 3.20
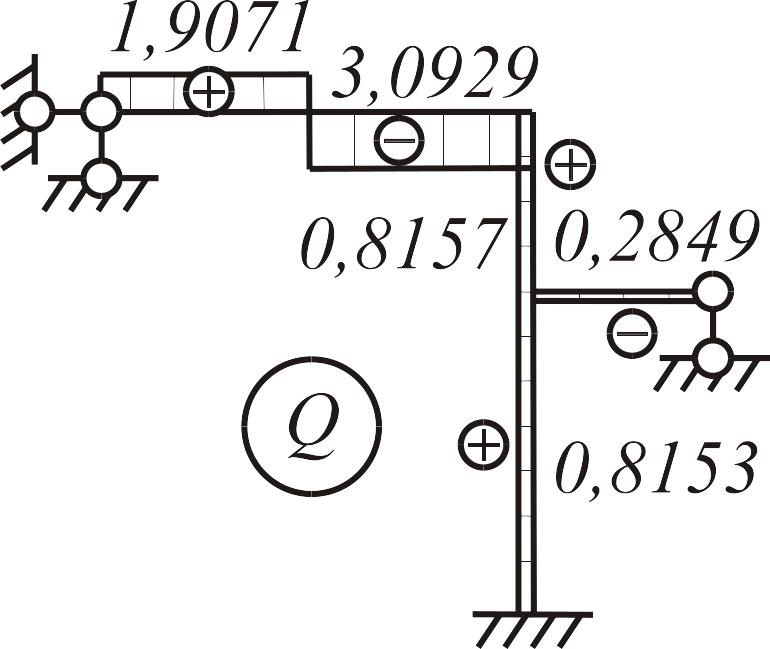
Эпюры и показаны на рис. 3.21 а, б.
а |
|
б |
|
Рис. 3.21
Рис. 3.22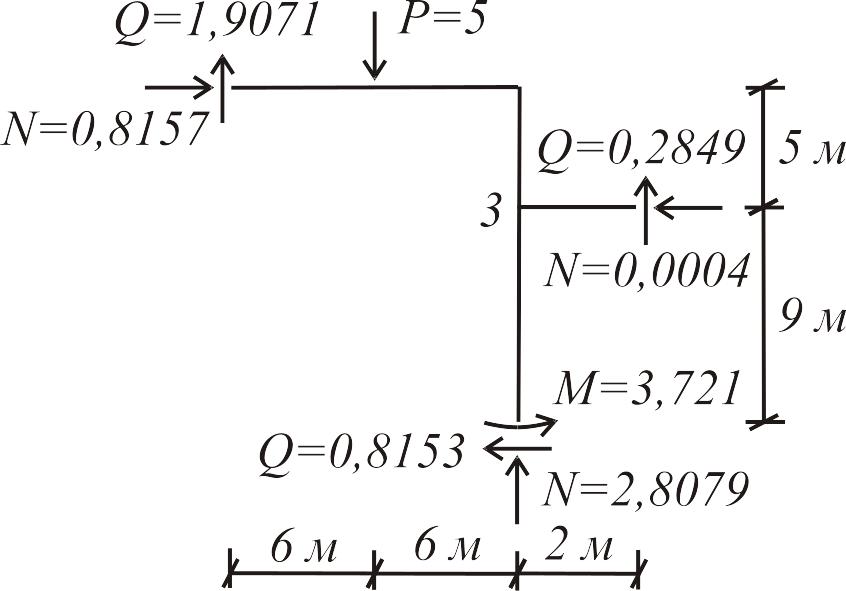
Составим три уравнения равновесия:
:
;
:
;
:
.
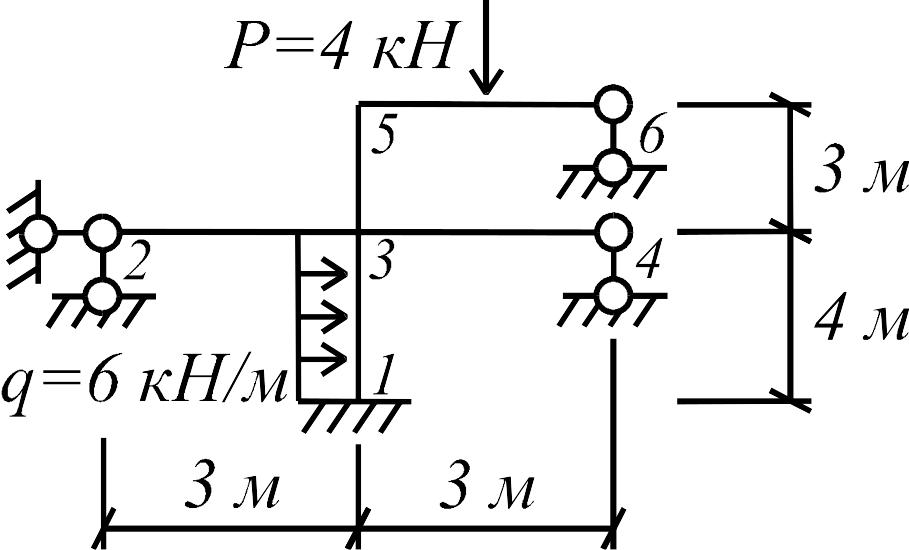
Задача 4. Требуется рассчитать статически неопределимую раму постоянной жесткости (рис. 3.23 а).
Решение. Для выбора рационального метода расчета вначале найдем общее число неизвестных по методам сил и перемещений.
Степень статической неопределимости -
.
Степень кинематической неопределимости -
.
Таким образом, рама четыре раза статически и три раза кинематически неопределима. Основные системы для методов сил и перемещений показаны на рис. 3.23 б, в соответственно.
а |
|
б |
|
в |
|
г |
|
Рис. 3.23
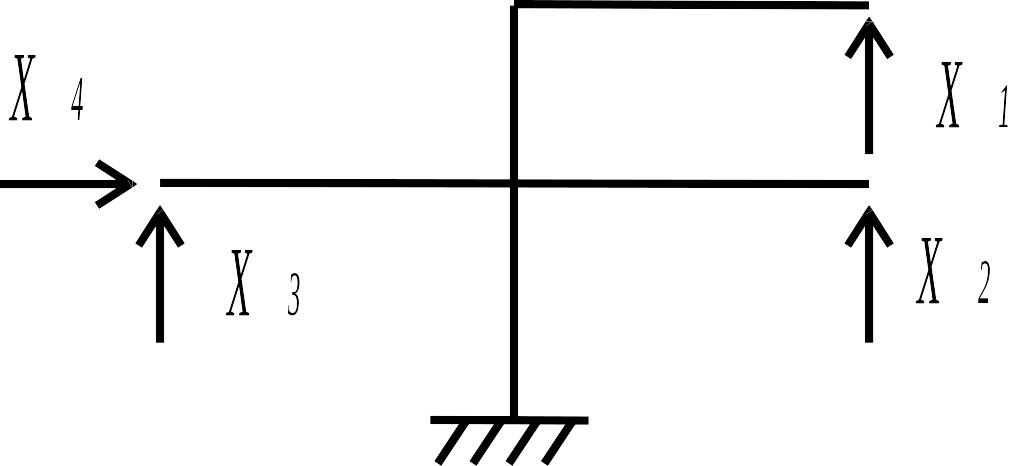
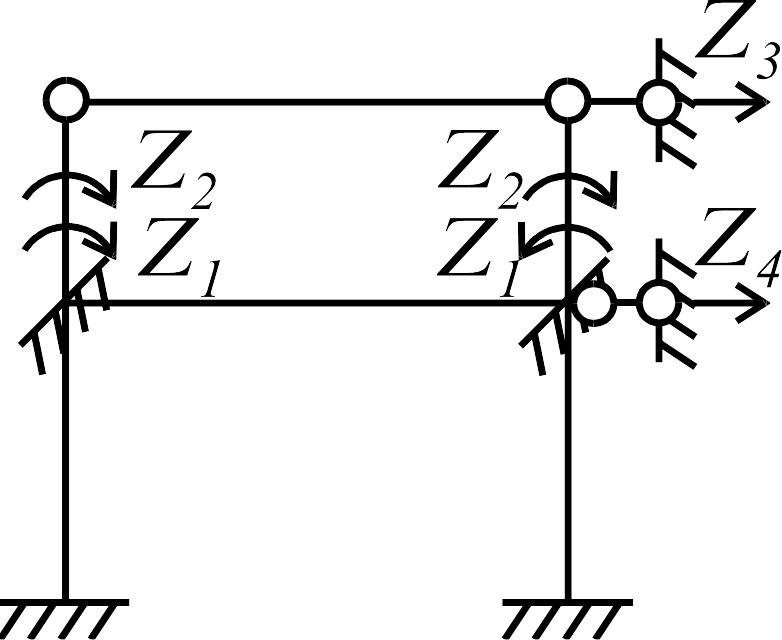
Определение общего числа неизвестных по смешанному методу. Для удобства подсчета мысленно проведем сечение 1 (рис. 3.23 г), «разделяющее» раму на две части, одна из которой обладает высокой статической, а другая высокой кинематической неопределимостью. В данном случае это будут нижняя и верхняя части соответственно. Результаты подсчета представим в табл. 6.
Таблица 6
Метод сил |
Метод перемещений |
Смешанный метод |
4 |
3 |
2 |
1 |
2 |
Верхняя часть |
3 |
1 |
Нижняя часть |
Как видно из данной таблицы, для верхней части более выгодным является метод сил, а для нижней - метод перемещений. Таким образом, рациональным является смешанный метод расчета. Окончательно имеем два неизвестных по смешанному методу: одно (по методу сил) в верхней части рамы и одно (по методу перемещений) в нижней ее части. Если применять только метод сил или только метод перемещений, то число неизвестных будет большим.
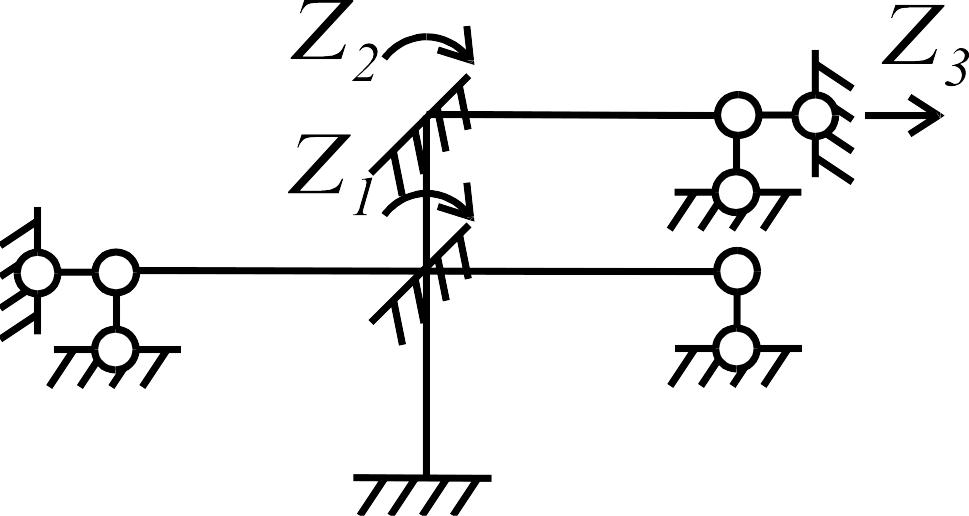
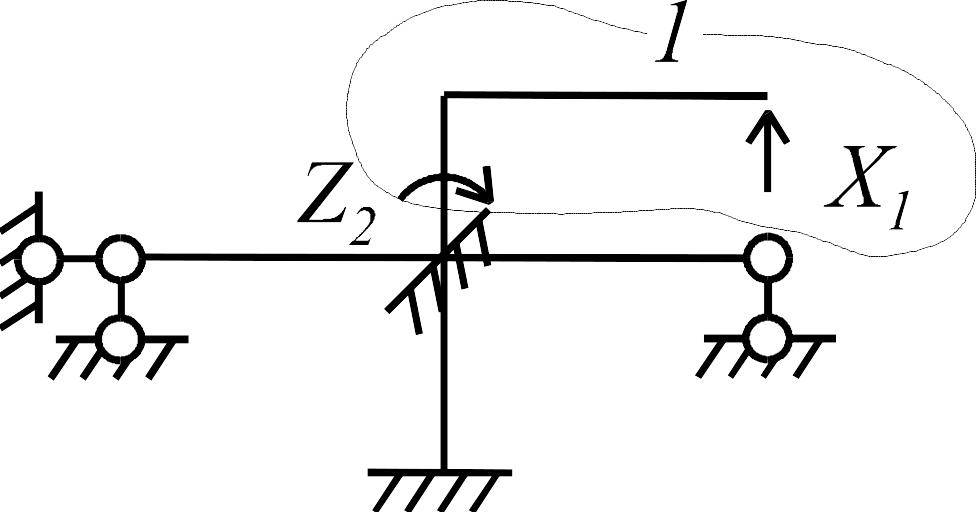
Основную
систему смешанного метода
получим из заданной следующим образом:
одновременно «отбросим» лишнюю связь
(вертикальный опорный стержень) в верхней
части рамы и введем дополнительную
связь (упругую заделку) в узел 3 ее нижней
части (рис. 3.23 г). Неизвестными приняты
реакция
в связи 6 и угол поворота
узла 3.
Составление канонических уравнений. Эквивалентность основной системы (рис. 3.23 г) заданной (рис. 3.23 а) выражается системой уравнений
Первое уравнение отрицает перемещение по направлению «отброшенной» связи, а второе - полную реакцию в дополнительной связи (заделке) от совместного действия , и заданной нагрузки.
Коэффициенты
,
называются смешанными. Коэффициент
определяется из условия равновесия
узла 3
с дополнительной связью, а
- из теоремы о совместности реакций и
перемещений, согласно которой
.
Смешанные коэффициенты метода сил
могут быть определены также и методом
векторной алгебры. Для этого искомое
перемещение
представляем в виде единичного вектора,
величина которого равна его моменту
относительно точки вращения.
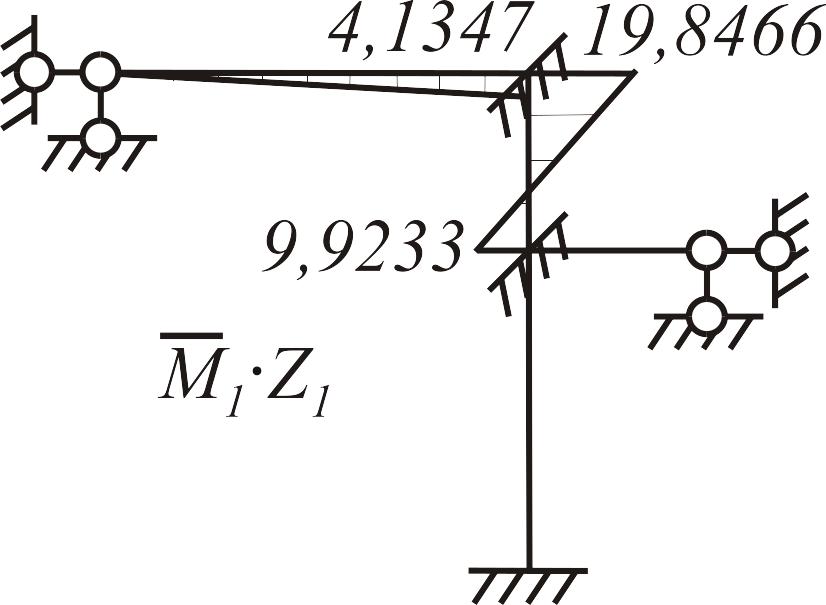
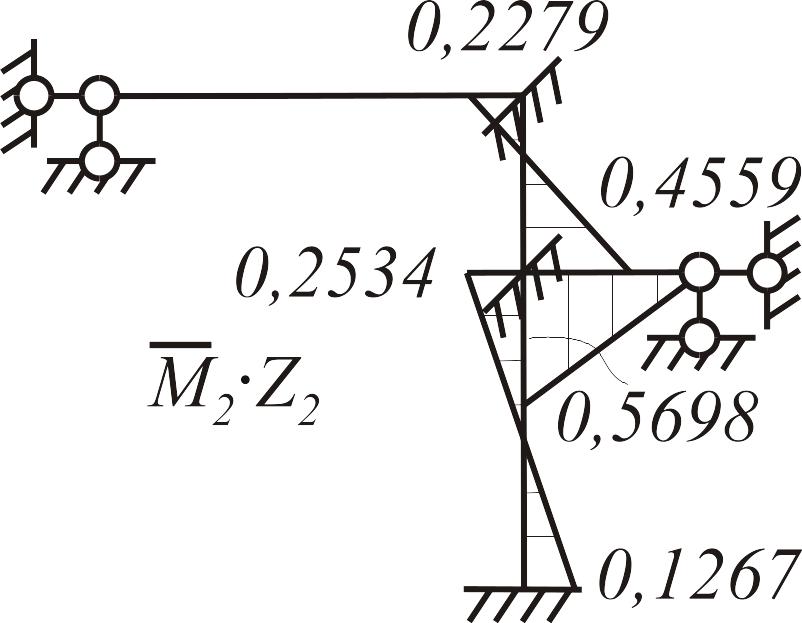
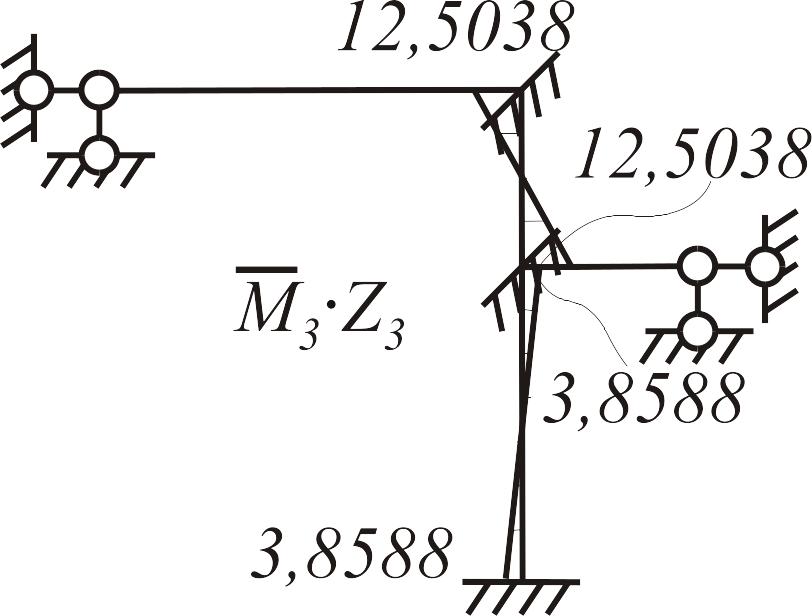
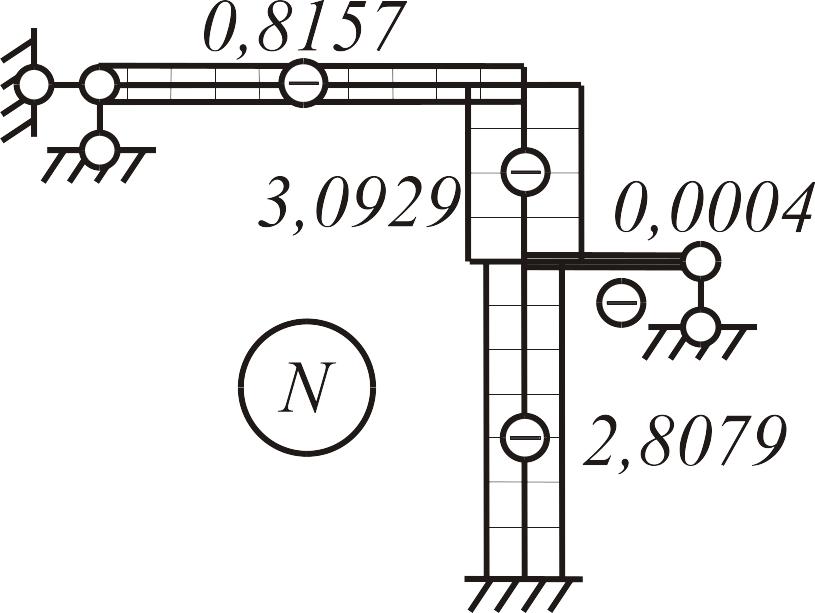
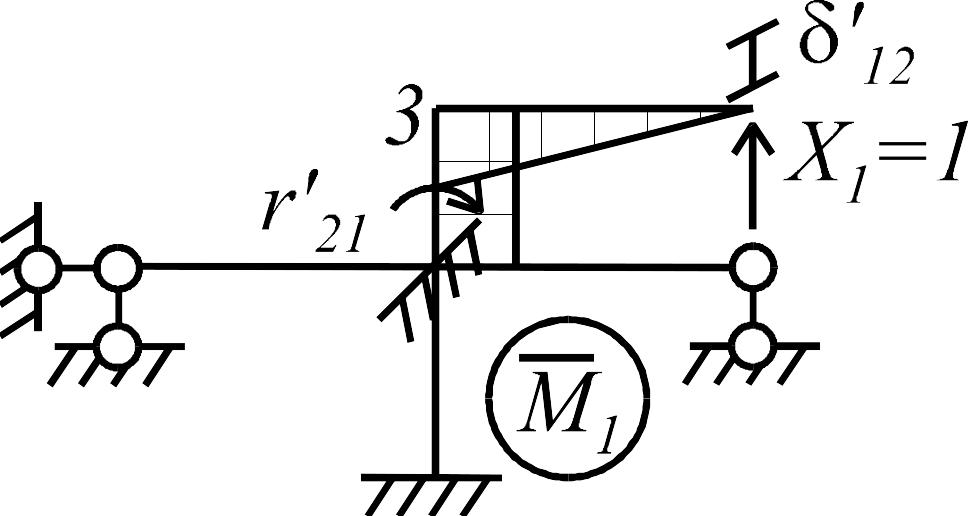
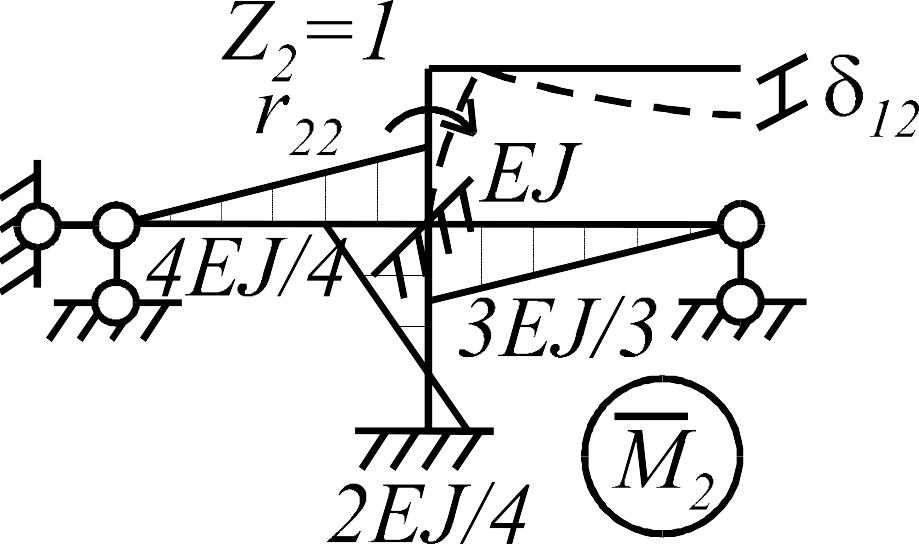
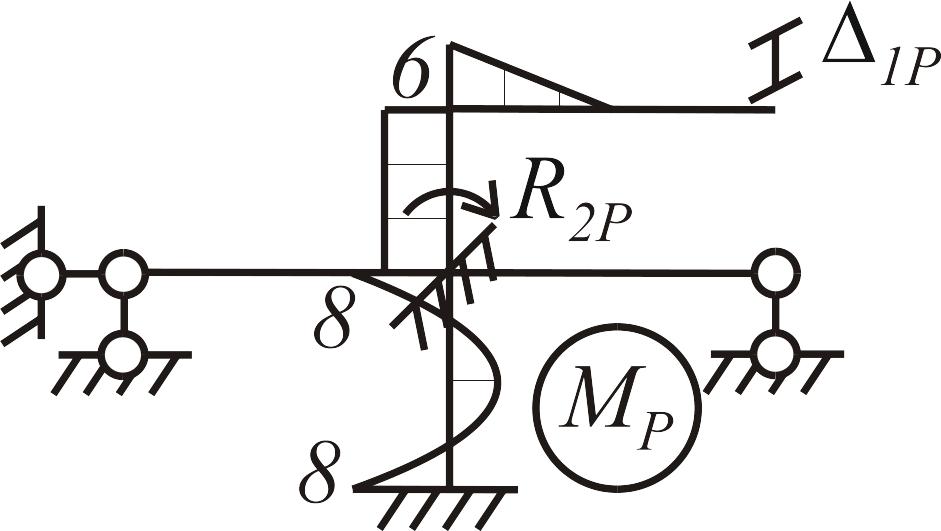
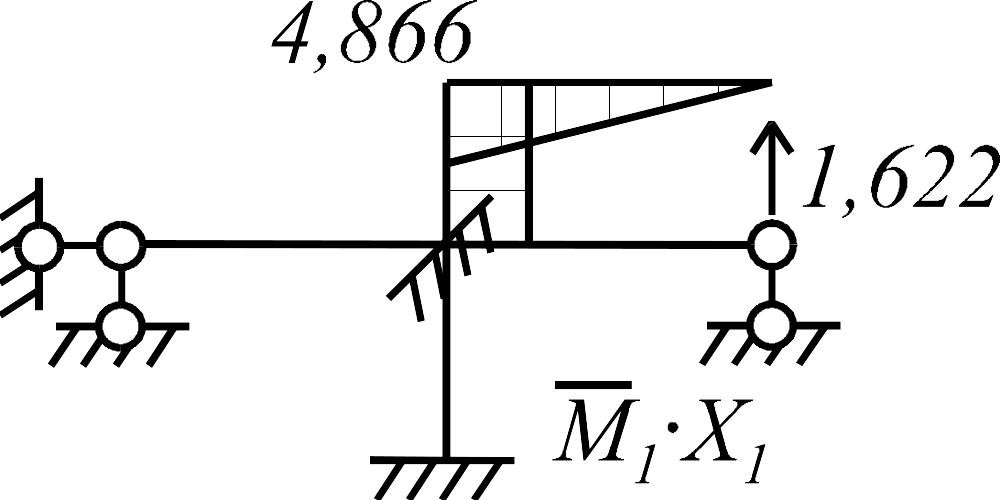
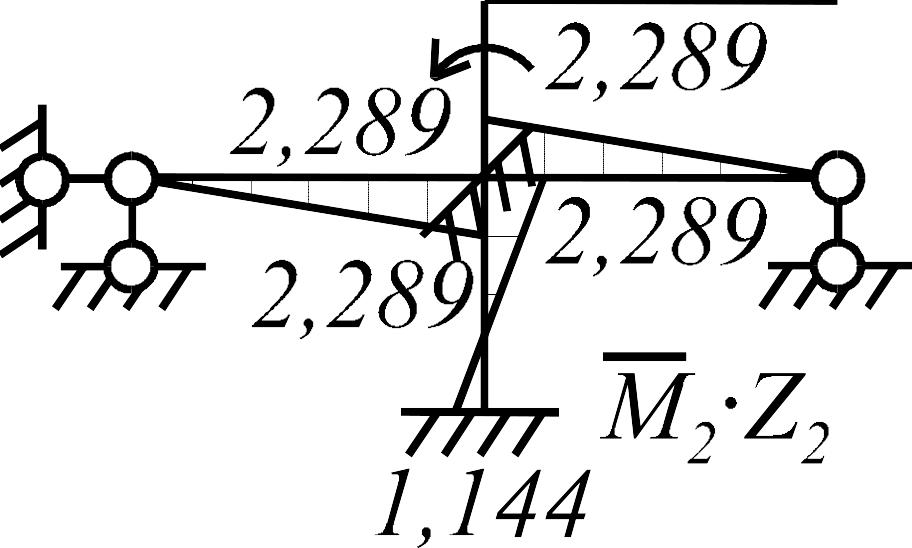
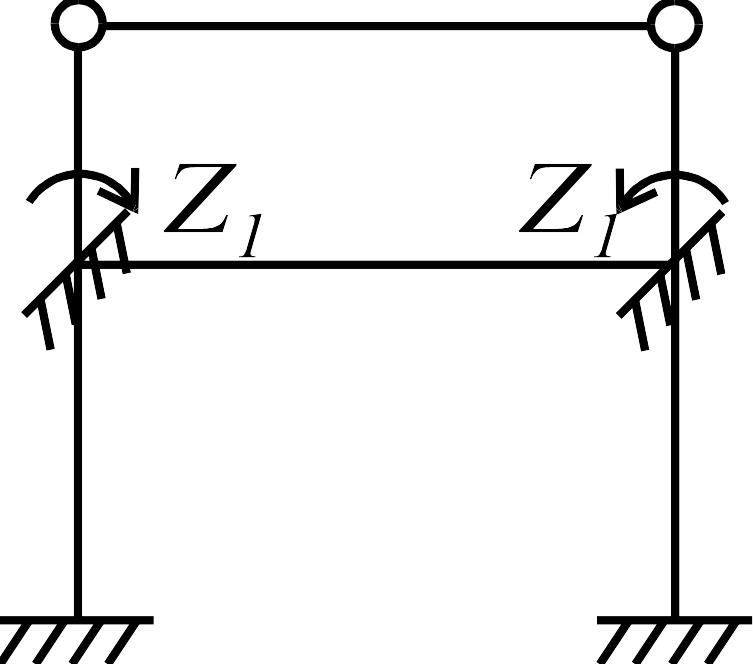
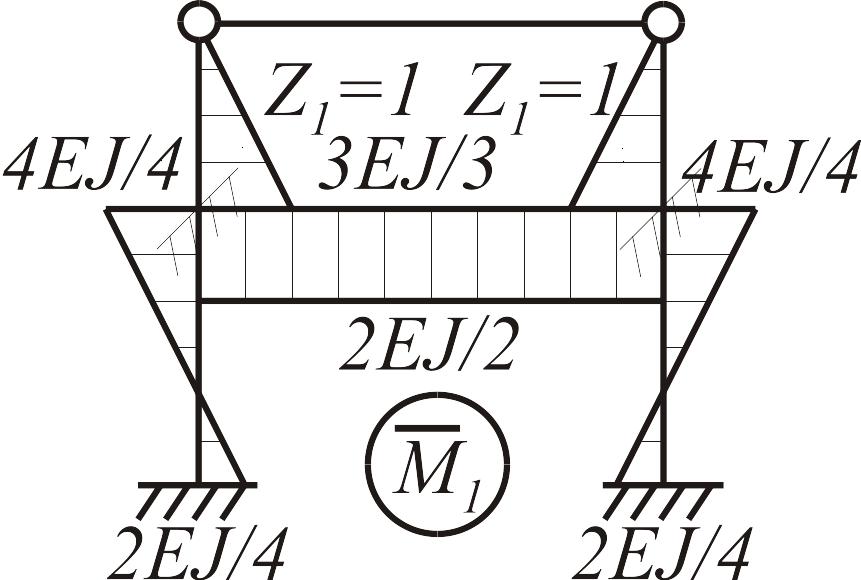
Построение единичных и грузовых эпюр в основной системе. В нижней части рамы, состоящей из статически неопределимых балок, единичные и грузовая эпюры строятся с использованием табличных решений, в верхней части (статически определимой) - методом сечений, рис.3.24.
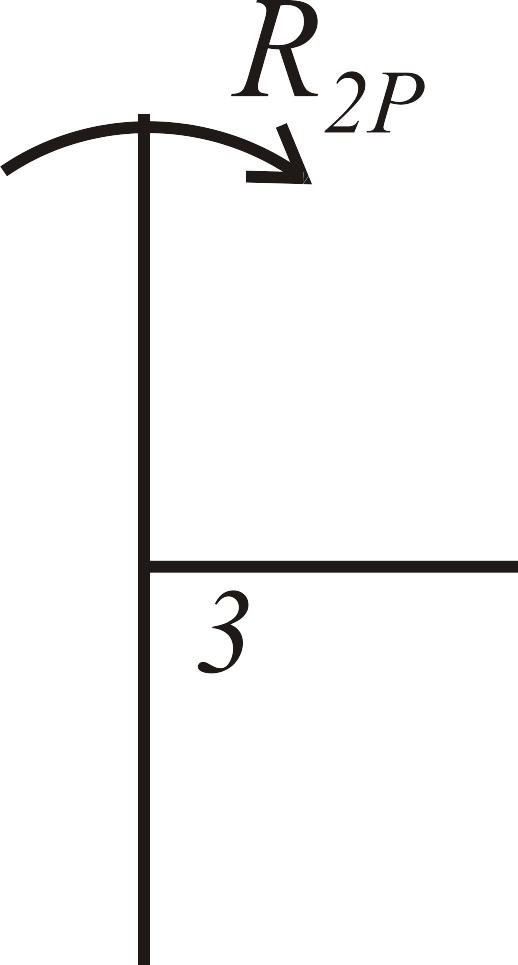
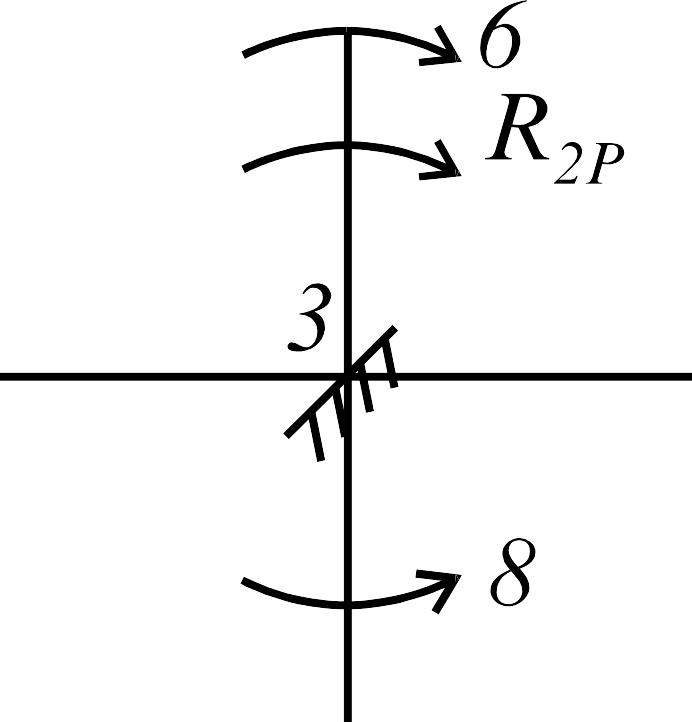
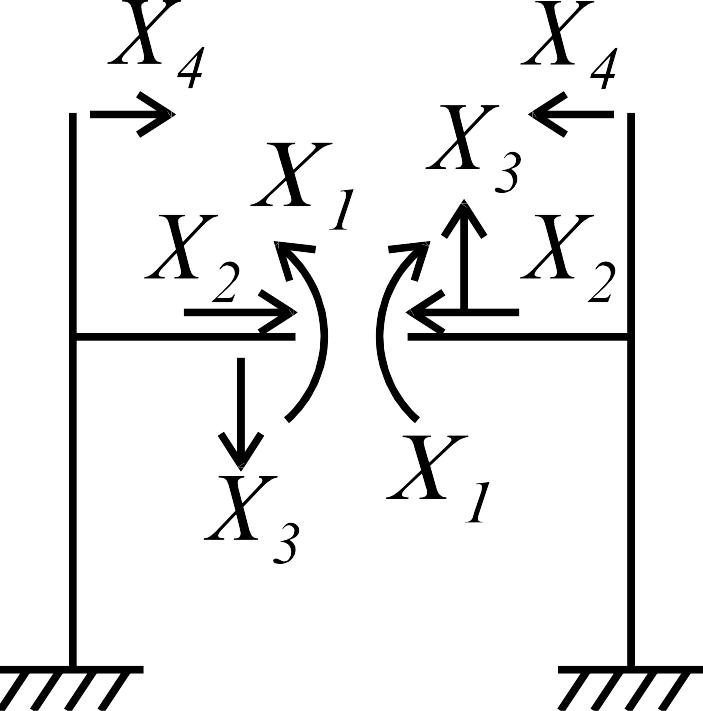
Коэффициенты канонических уравнений находим из условия равновесия узлов с дополнительными связями (рис. 3.25):
;
;
.
а |
б |
в |
|
|
|
Рис. 3.24
а |
|
б |
|
в |
|
Рис. 3.25
Коэффициенты
метода сил
определяем перемножением эпюр, используя
интеграл Мора и правило Верещагина.
Исключение составляют смешанные
коэффициенты метода сил
,
которые удобнее находить из зависимости
:
;
;
.
Система канонических уравнений решается любым из методов линейной алгебры (определителей, подстановки, Гаусса и др.)
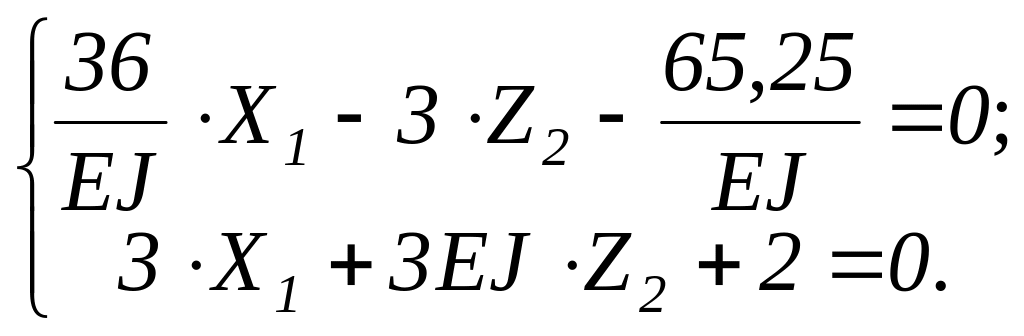
Окончательно имеем
,
.
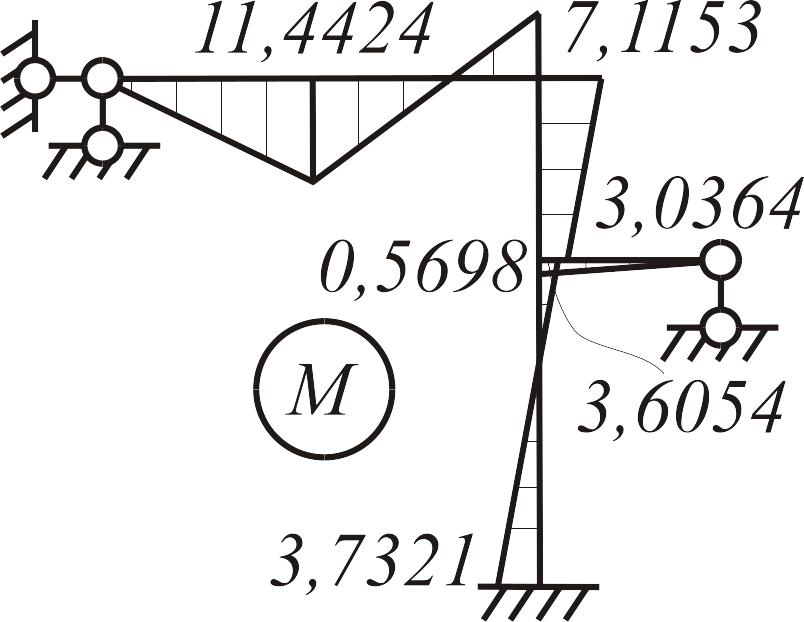
Действительную эпюру моментов строим в соответствии с принципом независимости действия сил (рис. 3.26):
.
а |
б |
в |
|
|
|
Рис. 3.26
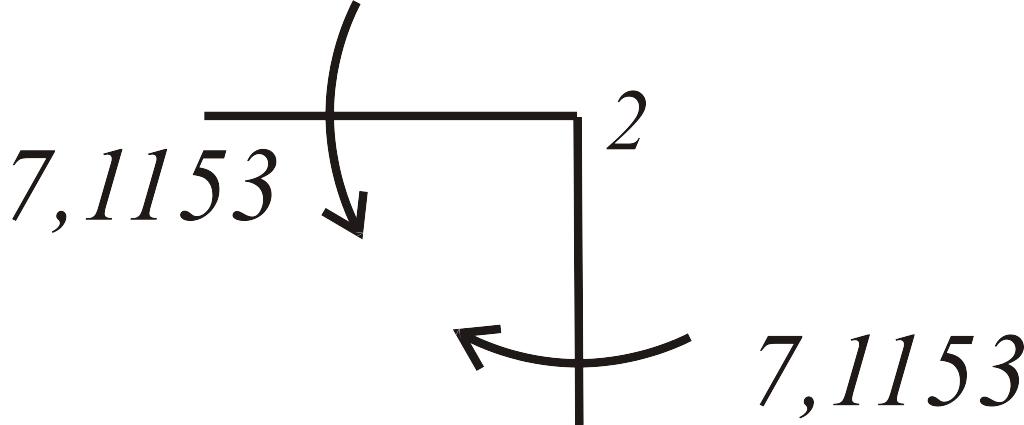
Для проверки правильности эпюры вырежем узлы 3 и 5 (рис. 3.27).
а |
|
б |
|
Рис. 3.27
Эпюры
и
строятся так же, как и в методе перемещений
(
,
- по значениям
из равновесия узлов рамы).
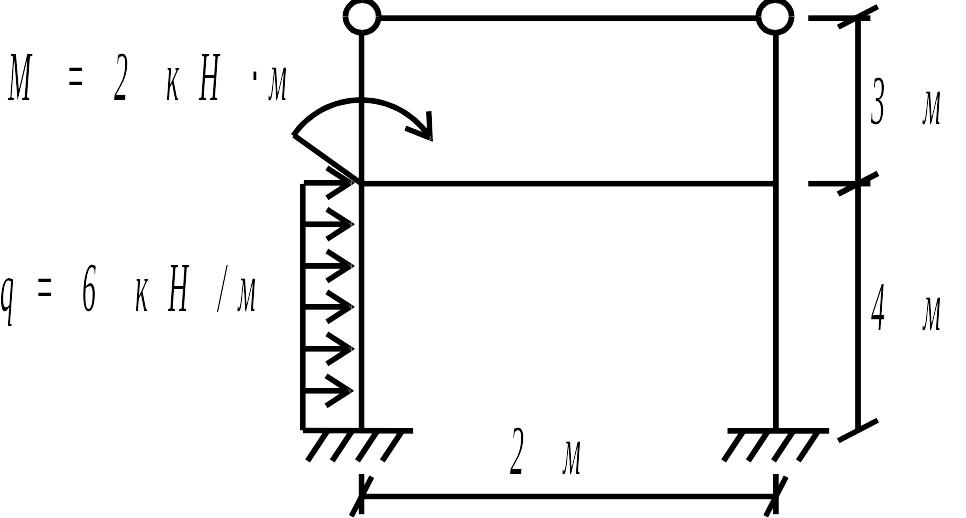
Задача 5. Рассчитать статически неопределимую раму (рис. 3.28 а) комбинированным методом.
а |
|
б |
|
||
в |
|
|
|||
Рис. 3.28
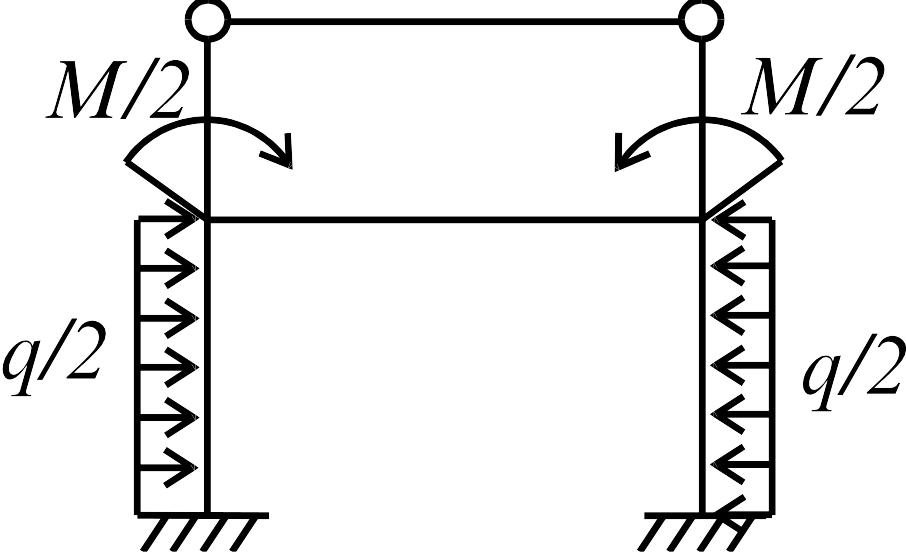
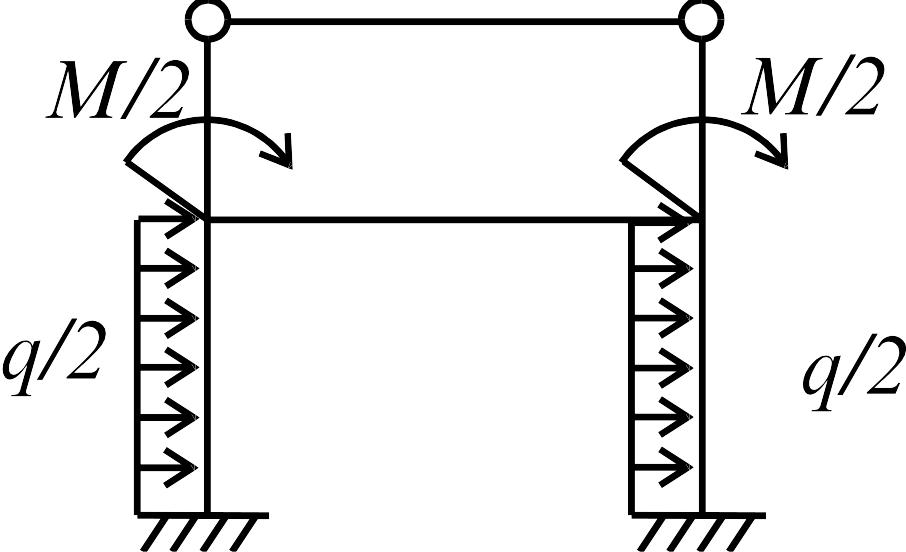
Решение. Разложим нагрузку на симметричную и кососимметричную составляющие (рис. 3.28 б, в). Число неизвестных для методов сил и перемещений показано в табл. 7 и на рис. 3.29 а, б.
Таблица 7
Метод расчета |
Количество неизвестных |
Всего |
|
симметричных |
кососимметричных |
||
Метод сил |
3 |
1 |
4 |
Метод перемещений |
1 |
3 |
4 |
Комбинированный метод |
1 |
1 |
2 |
На симметричную составляющую нагрузки раму рассчитаем методом перемещений и определим только симметричные неизвестные, т.к. кососимметричные равны нулю.
а |
|
б |
|
Рис. 3.29
На рис. 3.30 а, б, в показаны соответственно основная система метода перемещений с учетом симметрии, единичная и грузовая эпюры в ней.
а |
|
б |
|
в |
|
|
|
Рис. 3.30
а
б
Рис. 3.31
.
Коэффициенты вычисляем из условия равновесия узлов (рис. 3.31 а, б):
;
.
Решив уравнение
,
найдем
перемещение
.
Действительную эпюру изгибающих моментов от симметричной составляющей нагрузки построим, используя принцип наложения (рис. 3.32 а, б):
.
а |
|
б |
|
Рис. 3.32
На кососимметричную составляющую нагрузки раму рассчитаем методом сил, определяя только кососимметричное неизвестное, т.к. симметричные неизвестные обращаются в нуль.
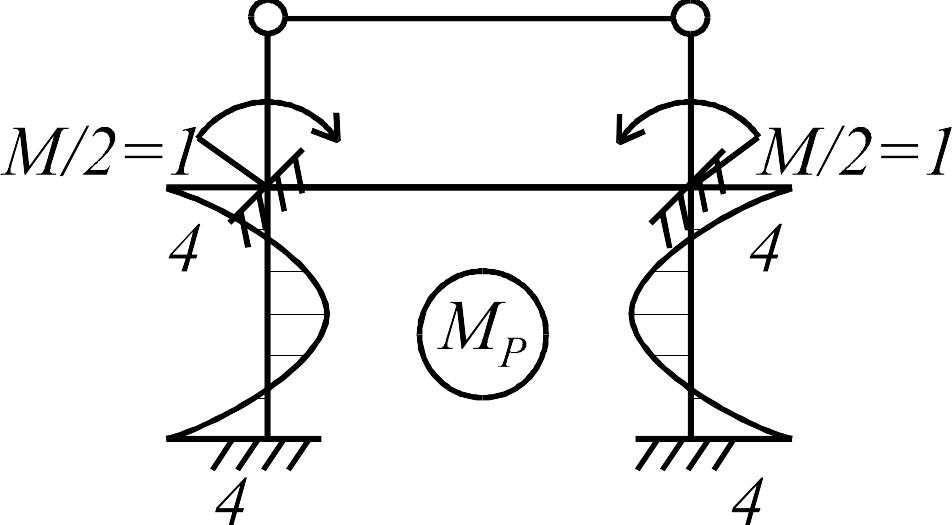
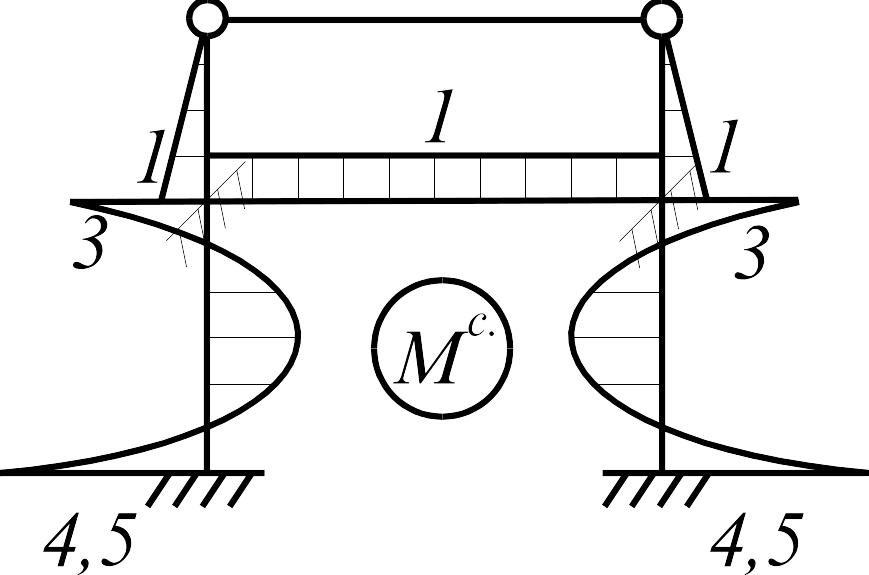
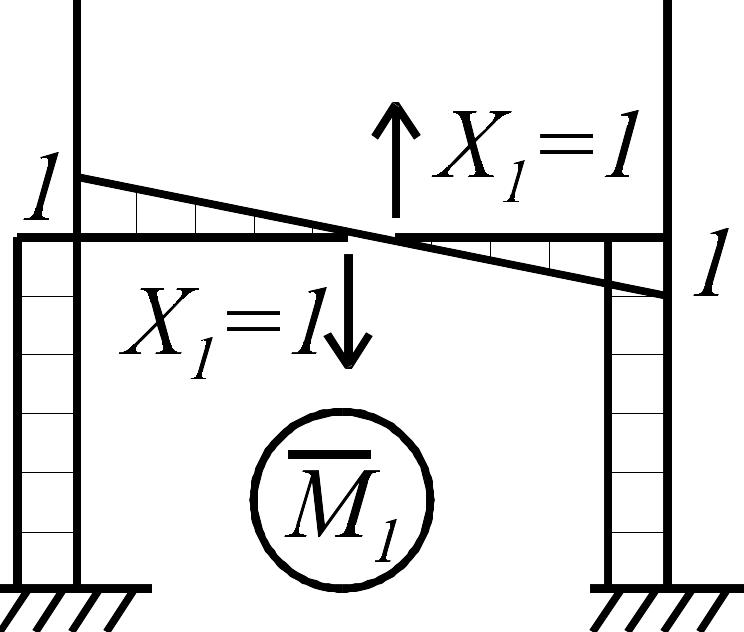
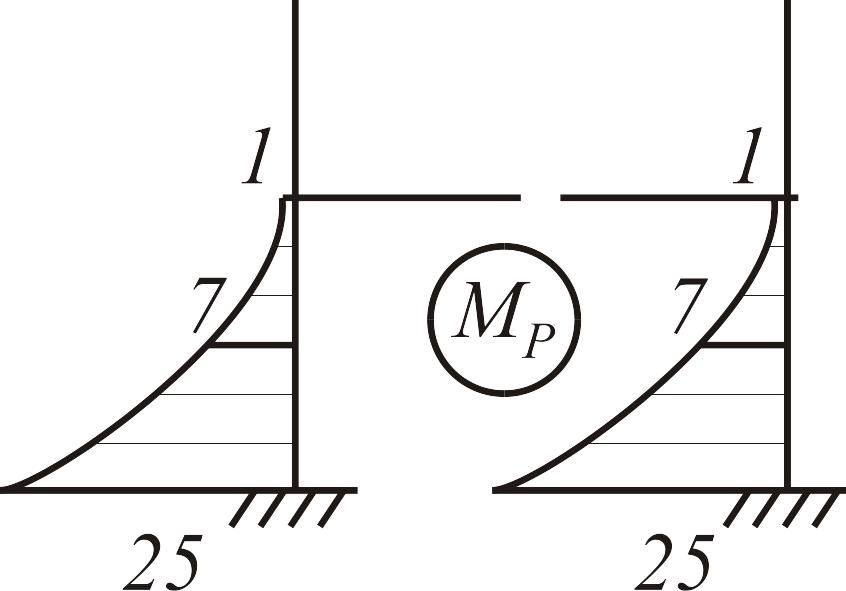
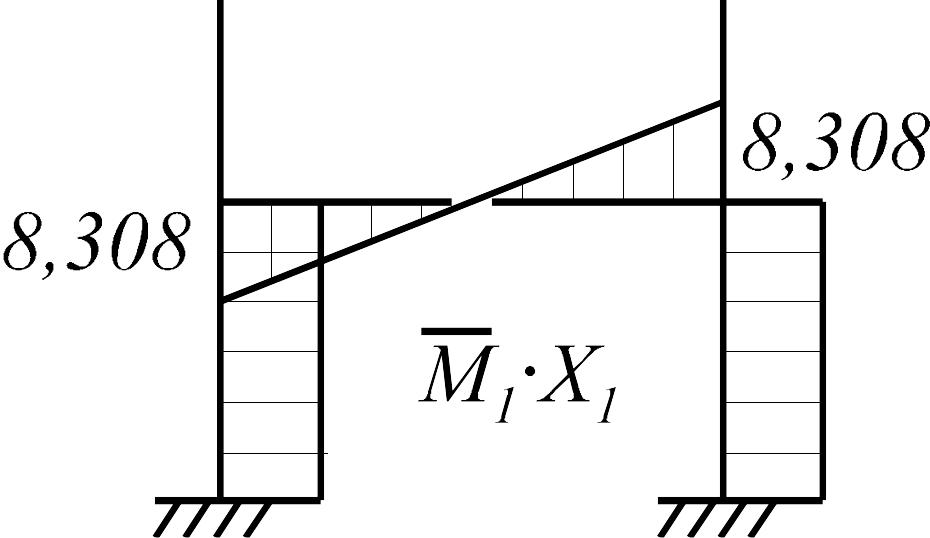
Основная система, единичная и грузовая эпюры для расчета методом сил с учетом симметрии показаны на рис. 3.33 а-в.
Уравнение метода сил примет вид
.
Коэффициенты уравнения вычислим по правилу Верещагина и правилу Симпсона:
;
.
а |
|
б |
|
в |
|
Рис. 3.33
Усилие в лишней связи найдем из уравнения
;
.
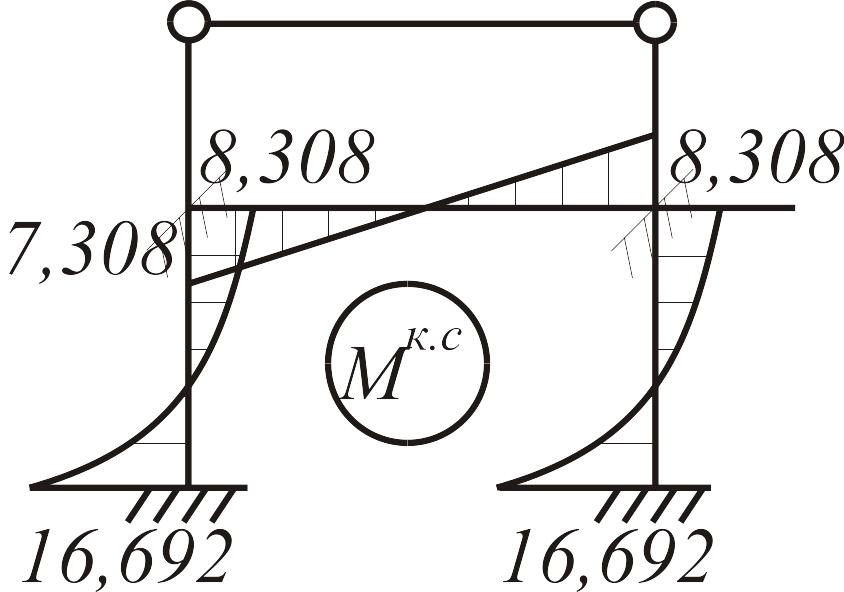
Действительную эпюру изгибающих моментов от кососимметричной составляющей нагрузки построим с помощью принципа наложения (рис. 3.34 а, б):
.
а |
|
б |
|
Рис. 3.35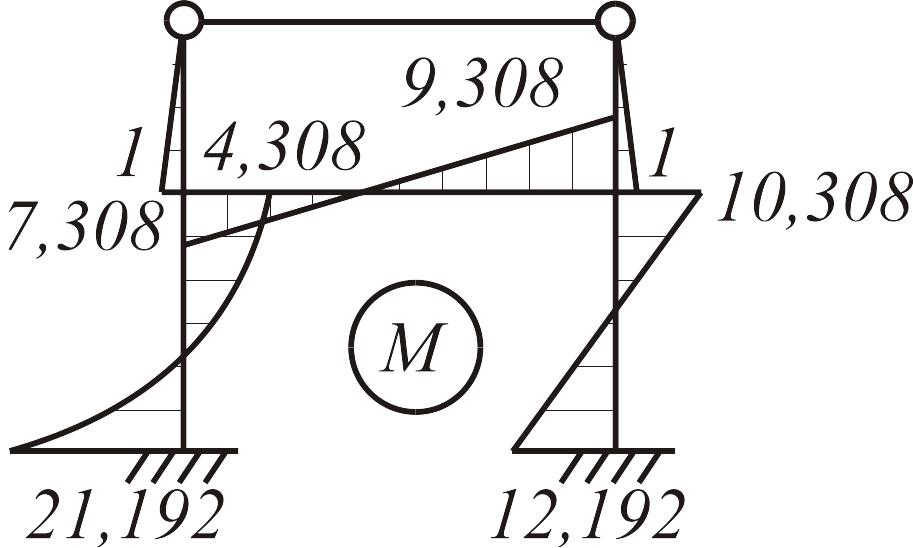
Действительную эпюру от заданной нагрузки построим сложением эпюр, полученных от симметричной и кососимметричной составляющих (рис. 3.35):
а
б
Рис. 3.36
.
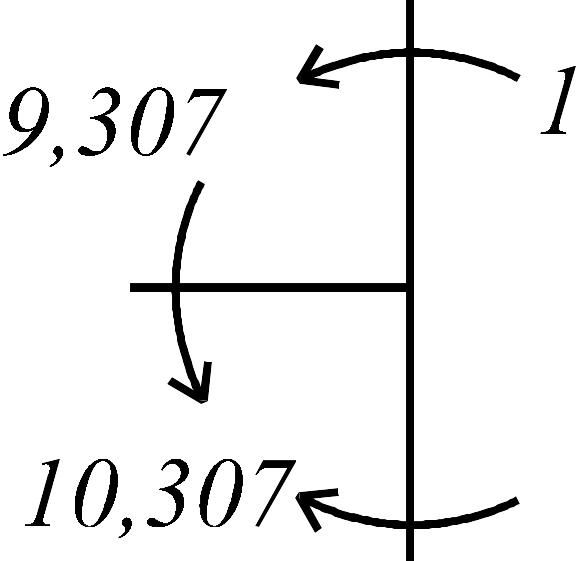
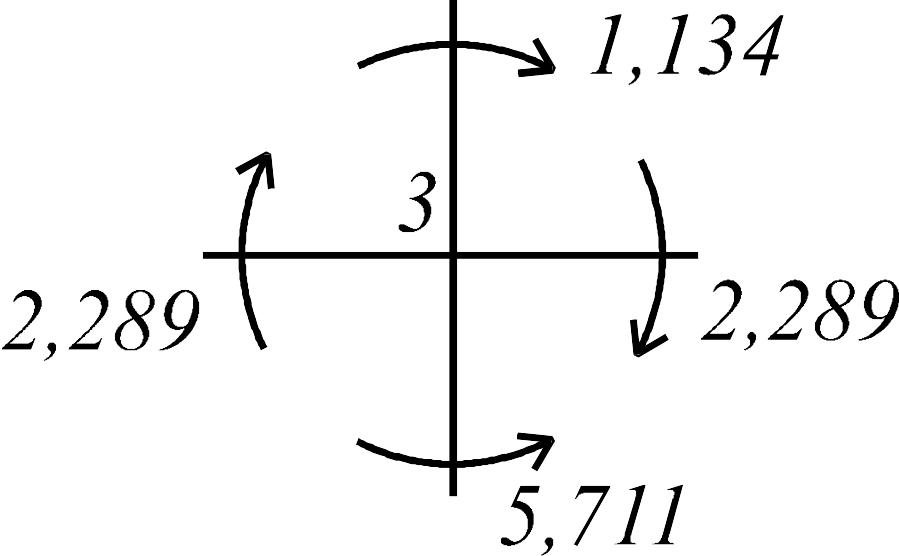
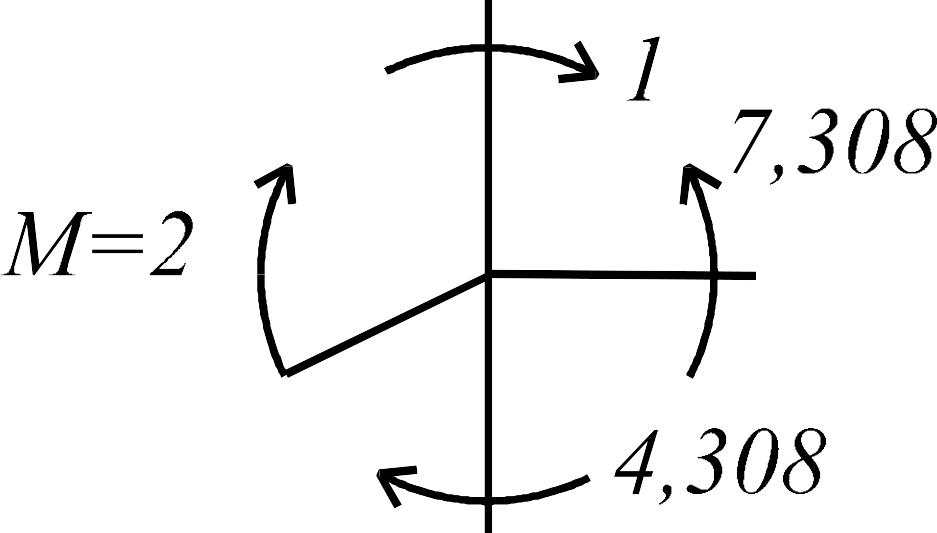
Проверка эпюры моментов для узлов рамы показана на рис. 3.36 а, б.
Эпюра
строится по эпюре
,
а эпюра
- по эпюре
.
Для систем, изображенных на рис. 1.12 б, в, подсчет неизвестных производить не будем. Для первой из них с учетом симметрии нагрузки предпочтительнее метод перемещений, а для второй - метод сил.
В системе, см. рис.
1.12 г, степень статической неопределимости
;
степень кинематической неопределимости
.
Наиболее эффективным при расчете
является комбинированный метод.
Системы, показанные на рис. 1.12 д-ж, следует рассчитывать смешанным методом.
Основные системы с приложенными неизвестными методов расчета всех разобранных схем показаны соответственно на рис. 1.13 а-ж.