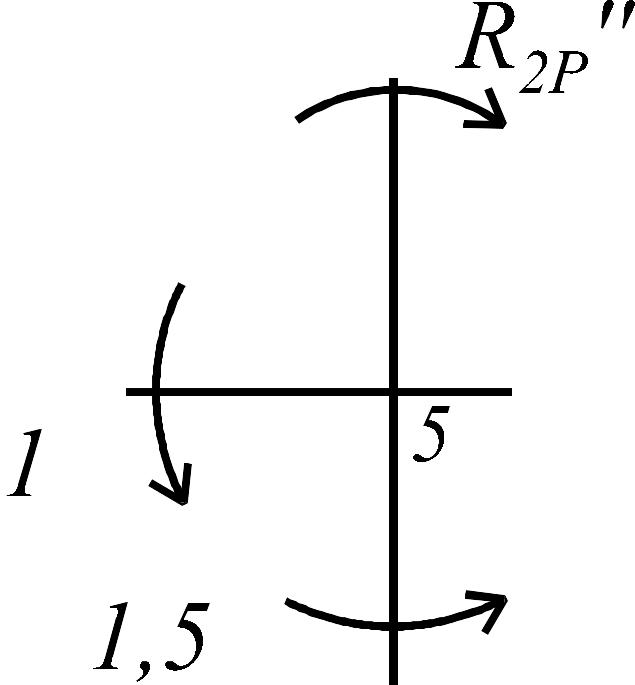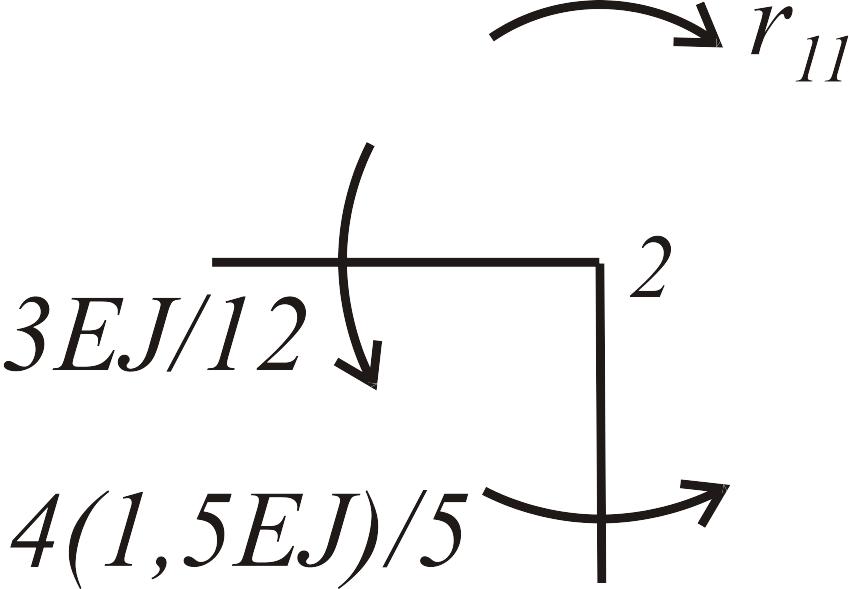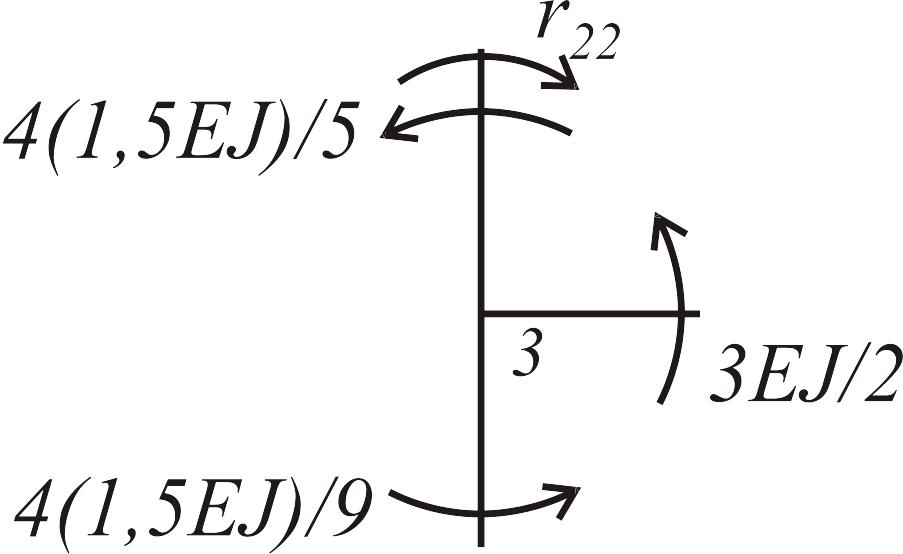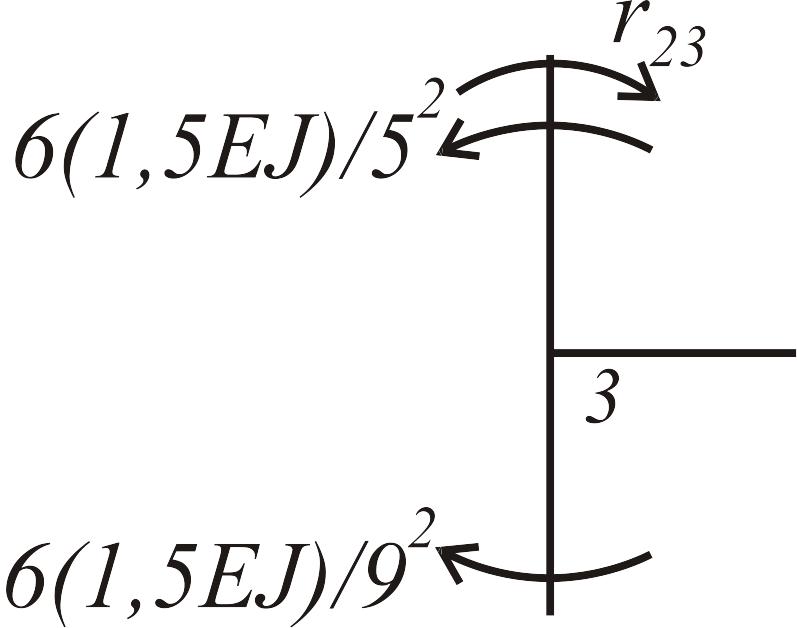- •13. Расчет статически неопределимых стержневых систем методом перемещений, смешанным и комбинированным методами
- •1. Основные положения методов перемещений, смешанного и комбинированного
- •1.1. Расчет статически неопределимых систем методом перемещений
- •1.1.1. Выбор неизвестных и основной системы
- •1.1.2. Система разрешающих уравнений в канонической форме
- •1.1.3. Вычисление коэффициентов системы канонических уравнений
- •1.1.4. Построение действительных эпюр внутренних усилий
- •1.1.5. Проверки расчетов
- •1.2. Особенности расчета симметричных рам
- •1.3. Особенности расчета статически неопределимых рам с наклонными стойками
- •1.4. Учет упругой податливости опор при расчете стержневых систем
- •1.5. Смешанный и комбинированный методы расчета статически неопределимых систем
- •Продолжение табл. 4
- •Окончание табл. 4
- •Окончание табл. 5
Продолжение табл. 4
Схема |
Уравнения равновесия |
Величина коэффициента |
Состояние
3 (эпюра
|
|
|
Состояние
1 (эпюра
|
:
:
|
|
Состояние 2 (эпюра )
|
:
:
|
|
Состояние 3 (эпюра )
|
:
:
|
|
Состояние 1 (эпюра )
|
|
|
Состояние 2 (эпюра )
|
:
|
|
Состояние 3 (эпюра )
|
:
|
|
Окончание табл. 4
Схема |
Уравнения равновесия |
Величина коэффициента |
|
Грузовое состояние (эпюра ) |
|
|
|
|
|
:
:
|
|
Грузовое состояние (эпюра ) |
|
|
|
|
|
:
:
|
|
Грузовое состояние (эпюра )
|
:
|
|
|
Подставив значения коэффициентов в систему канонических уравнений, получим одно уравнение с симметричным неизвестным и систему двух уравнений с кососимметричными неизвестными, независимых друг от друга:
![]() ;
;

В результате решения находим значения неизвестных:
![]() ,
,
![]() ,
,
![]() .
.
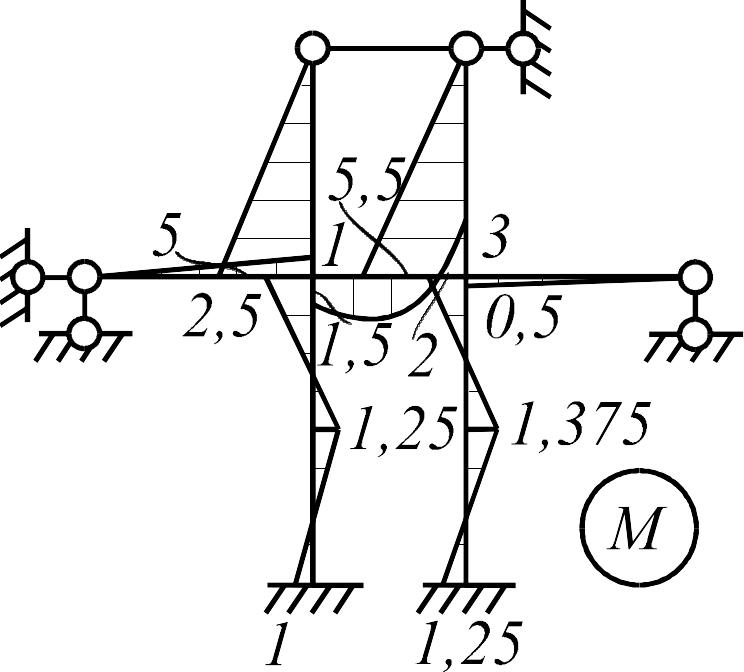
Действительную (окончательную) эпюру (рис. 3.13 г) строим способом наложения, складывая грузовую и исправленные эпюры (рис. 3.13 а-в).
а |
|
б |
|
в |
|
г |
|
Рис. 3.13
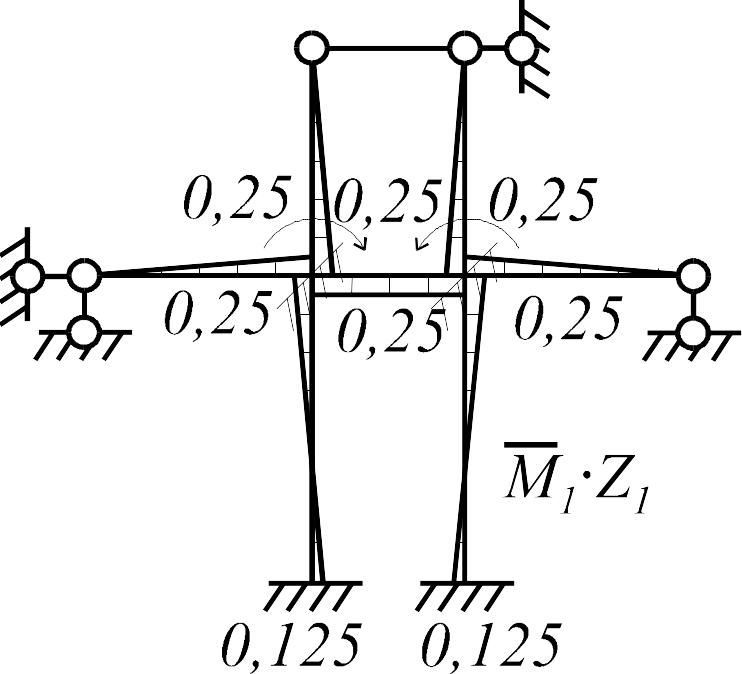
Выполняем статическую проверку эпюры . Для этого вырезаем узлы 4 и 5 на эпюре (рис. 3.14) и рассматриваем их равновесие.
а |
б |
|
|
Рис. 3.14
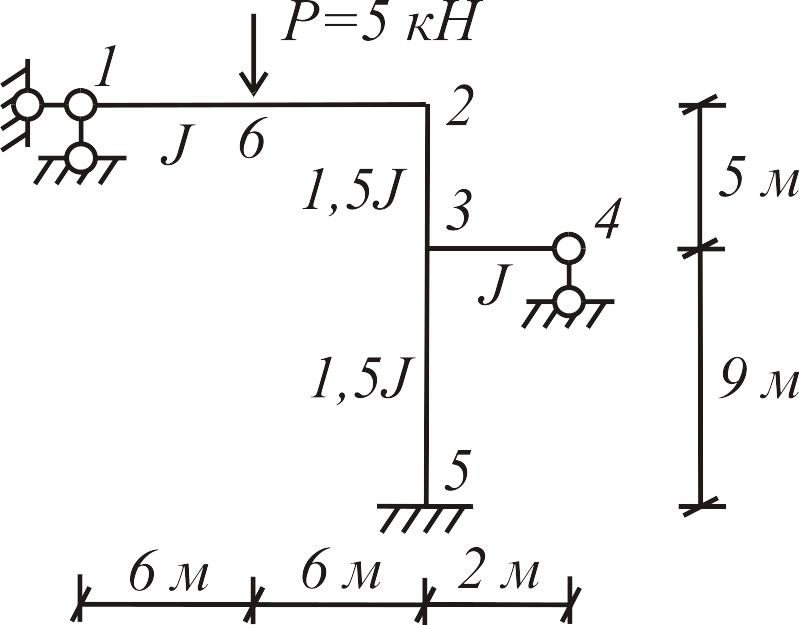
Задача
3. Для рамы
(рис. 3.15) построить эпюры
![]() ,
,
![]() ,
,
![]() методом перемещений и выполнить
необходимые проверки.
методом перемещений и выполнить
необходимые проверки.
а |
|
б |
|
|
в |
|
|
||
Рис.3.15
Решение.
Определим число неизвестных метода
перемещений. Число неизвестных углов
поворота
![]() ,
так как заданная рама имеет два жестких
узла. Для определения числа независимых
линейных смещений
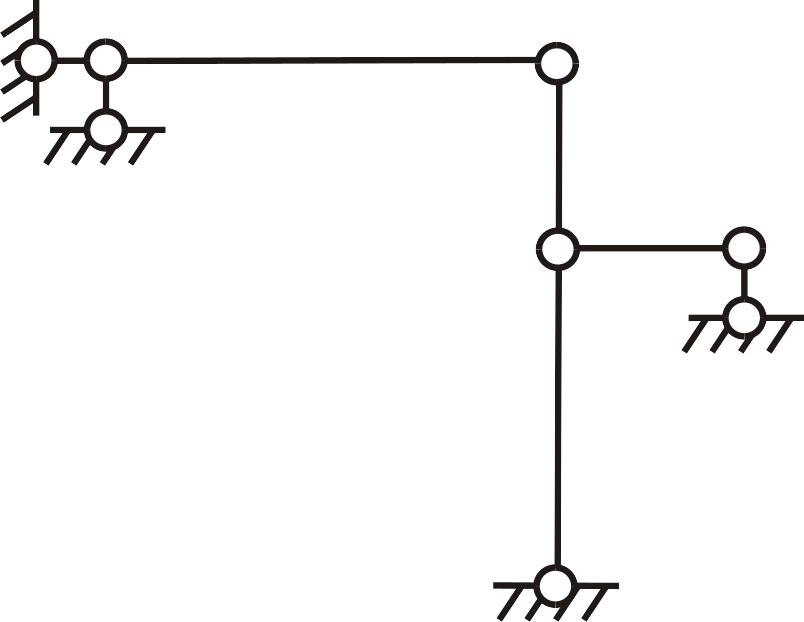
врезаем во все жесткие узлы рамы (рис.
3.15 а), включая опорные, шарниры. В итоге
рама превращается в шарнирно-стержневую
систему (рис.3.15 б).
,
так как заданная рама имеет два жестких
узла. Для определения числа независимых
линейных смещений
врезаем во все жесткие узлы рамы (рис.
3.15 а), включая опорные, шарниры. В итоге
рама превращается в шарнирно-стержневую
систему (рис.3.15 б).
Для
того чтобы преобразовать шарнирную
схему в геометрически неизменяемую
систему, достаточно ввести один опорный
стержень, препятствующий горизонтальному
смещению узлов 3,
4. Таким
образом, заданная рама имеет одно
независимое линейное перемещение:
![]()
![]() .
Общее число неизвестных
.
Общее число неизвестных
![]() ,
т.е. рама трижды кинематически неопределима.
,
т.е. рама трижды кинематически неопределима.
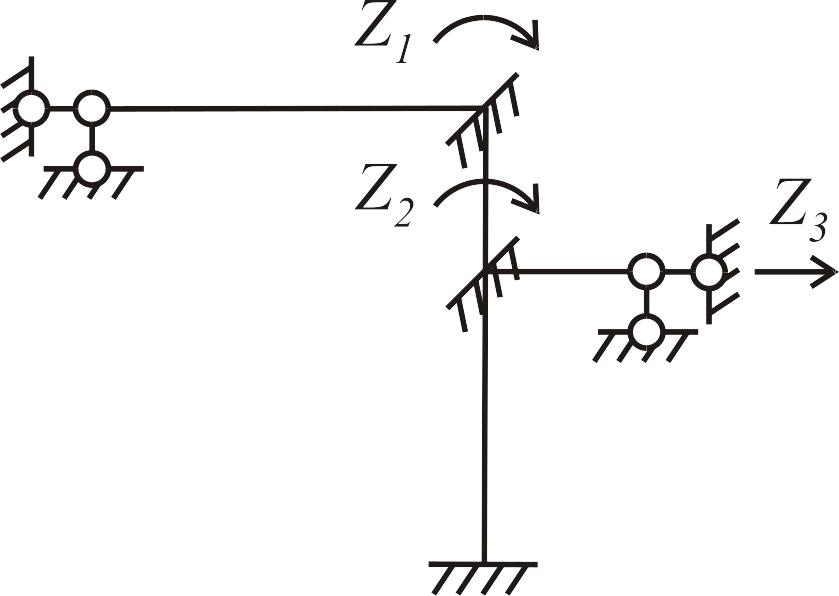
Образуем
основную
систему метода перемещений.
Для этого введем в жесткие узлы 2,
3 дополнительные
упругие заделки, препятствующие повороту
узлов, а по направлению линейного
смещения (вдоль ригеля рамы) - горизонтальную
связь, препятствующую ему (рис. 3.15 в).
Обозначим неизвестные: углы поворота
упругих заделок -
![]() ,
,
![]() ,
линейное смещение -
,
линейное смещение -
![]() (рис. 3.15 в).
(рис. 3.15 в).
Запишем систему канонических уравнений метода перемещений:

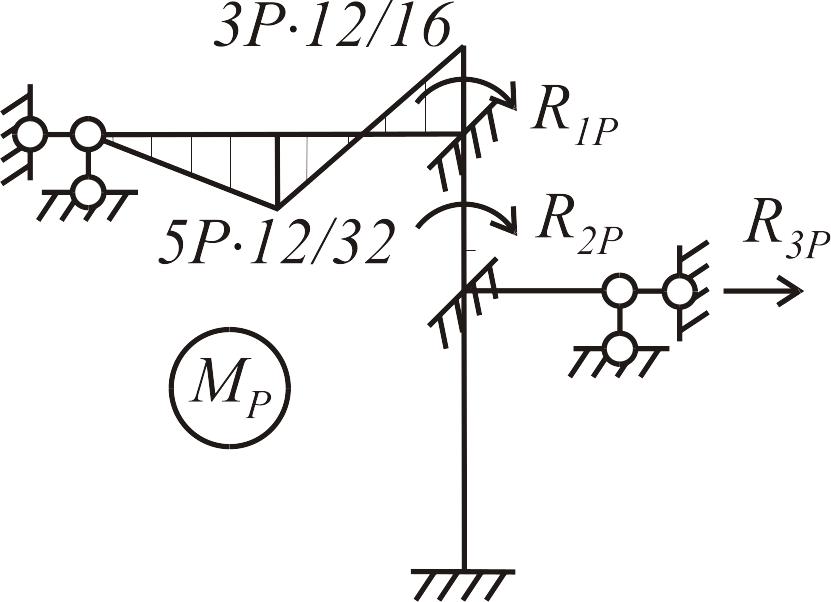
Для
определения ее коэффициентов
строим
единичные и грузовую эпюры изгибающих
моментов в основной системе. Для единичных
эпюр
,
,
![]() используем табл. 1, задавая упругим
заделкам единичные углы поворота
,
по ходу часовой стрелки (рис. 3.16 а), а по
направлению введенной линейной связи
- перемещение
используем табл. 1, задавая упругим
заделкам единичные углы поворота
,
по ходу часовой стрелки (рис. 3.16 а), а по
направлению введенной линейной связи
- перемещение
![]() (рис. 3.16 б). Грузовая эпюра
имеется только на тех стержнях, к которым
приложена внешняя нагрузка (рис. 3.16 в).
(рис. 3.16 б). Грузовая эпюра
имеется только на тех стержнях, к которым
приложена внешняя нагрузка (рис. 3.16 в).
а |
|
б |
|
в |
|
г |
|
Рис.3.16
Найдем
единичные и грузовые коэффициенты
первого (
,
![]() ,
,
![]() ,
,
![]() ),
второго (
),
второго (![]() ,
,
![]() ,
,
![]() ,
,
![]() )
и третьего (
)
и третьего (![]() ,
,
![]() ,
,
![]() ,
,
![]() )
уравнений, рассматривая соответственно
равновесие узлов 2, 3 и горизонтальной
отсеченной части рамы. Результаты сведем
в табл. 5.
)
уравнений, рассматривая соответственно
равновесие узлов 2, 3 и горизонтальной
отсеченной части рамы. Результаты сведем
в табл. 5.
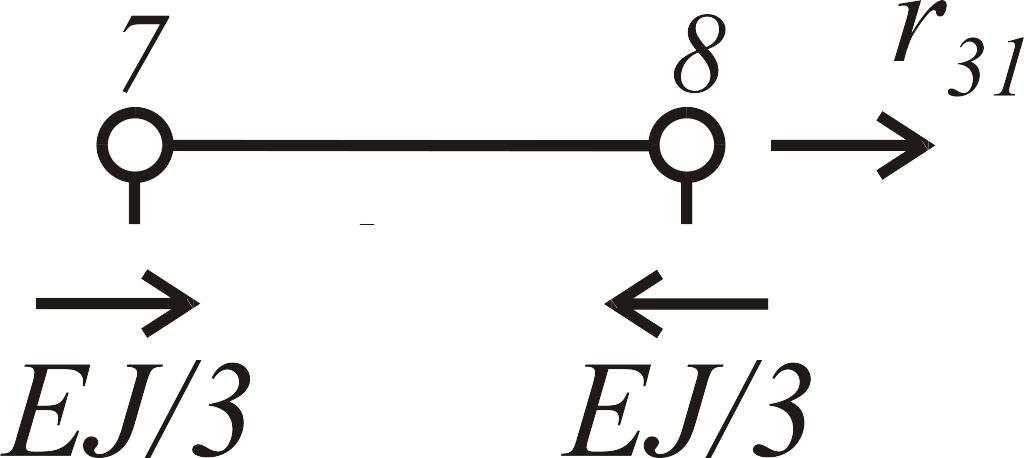
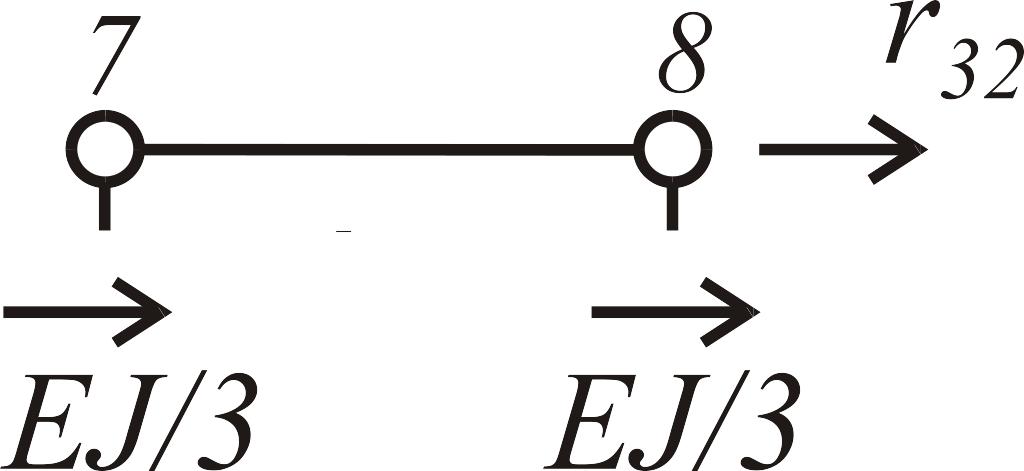
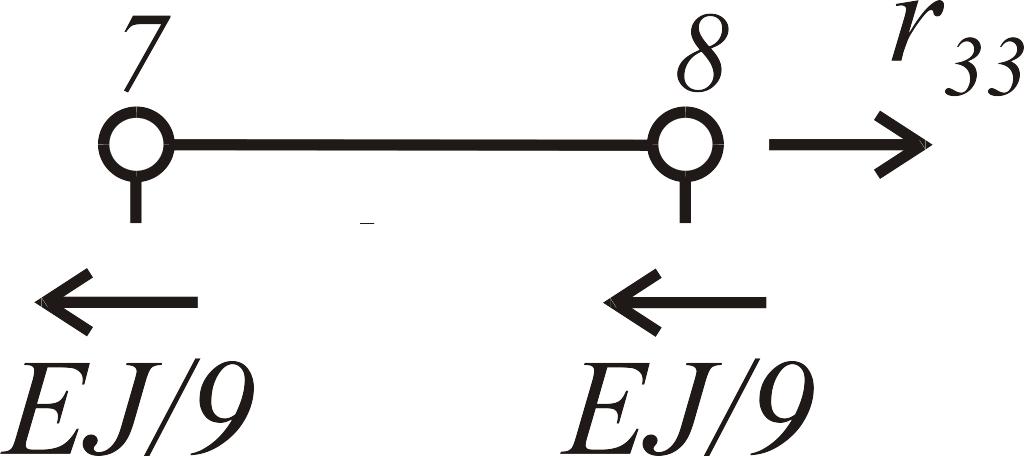
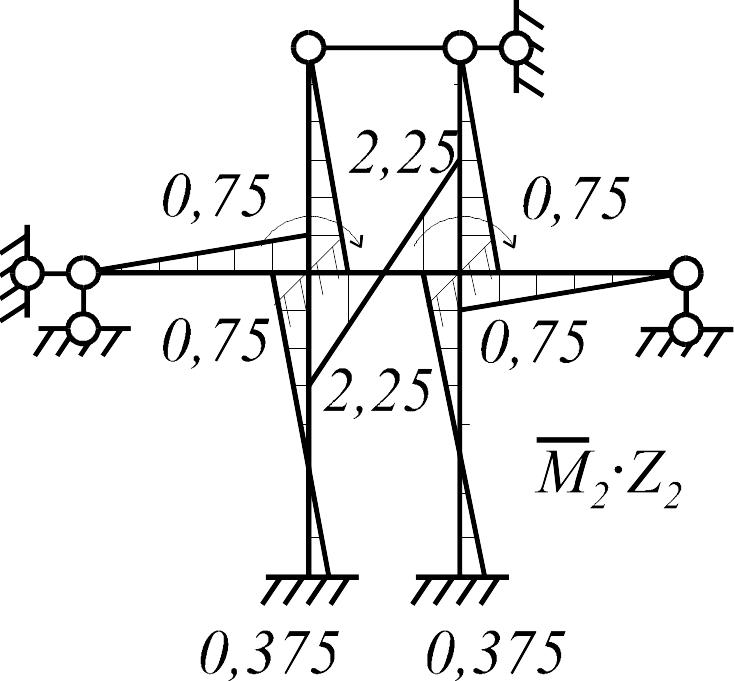
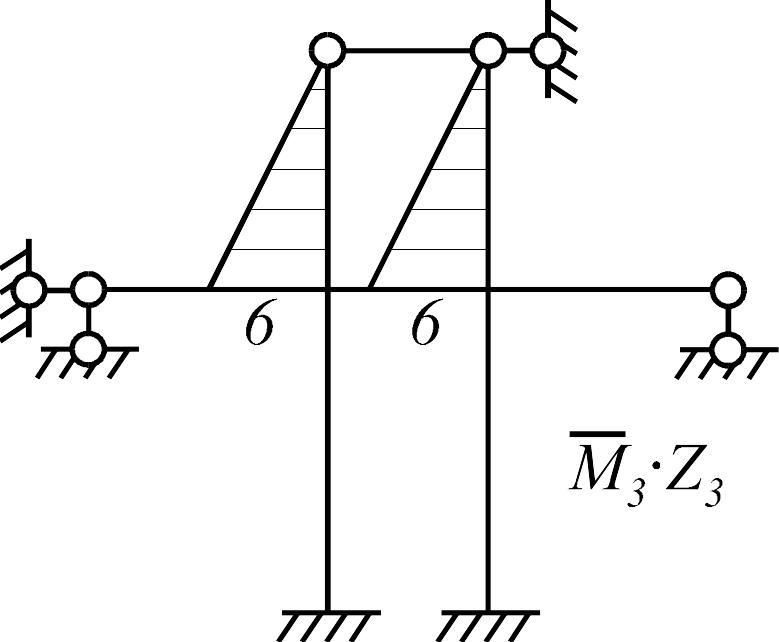
Таблица 5
Схема |
Уравнения равновесия |
Величина коэффициента |
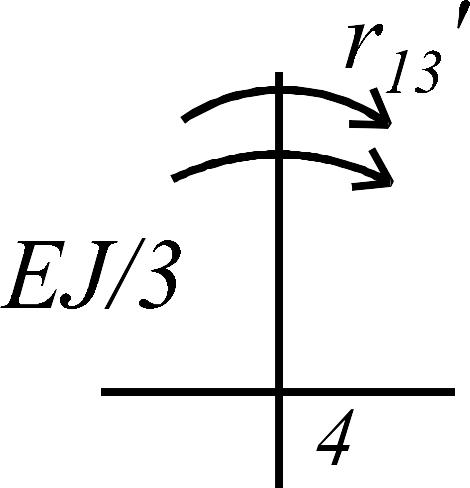
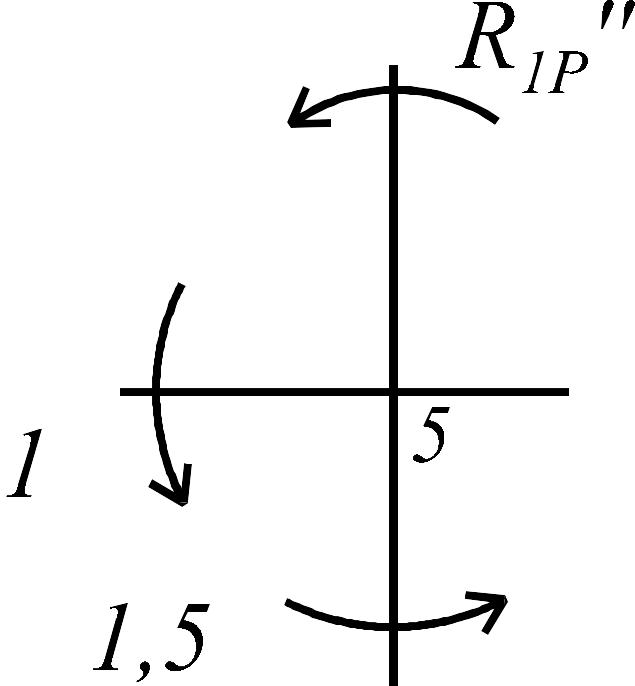
Состояние 1 (эпюра )
|
|
|
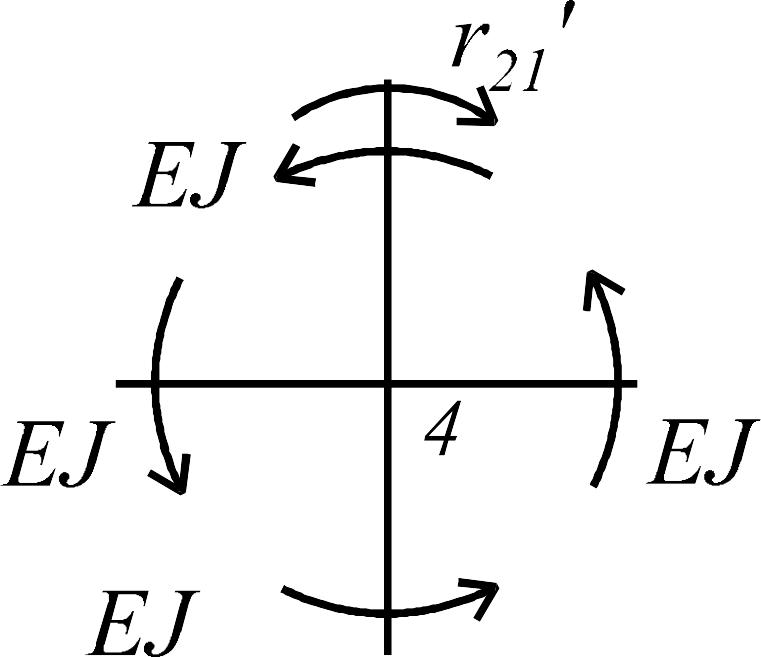
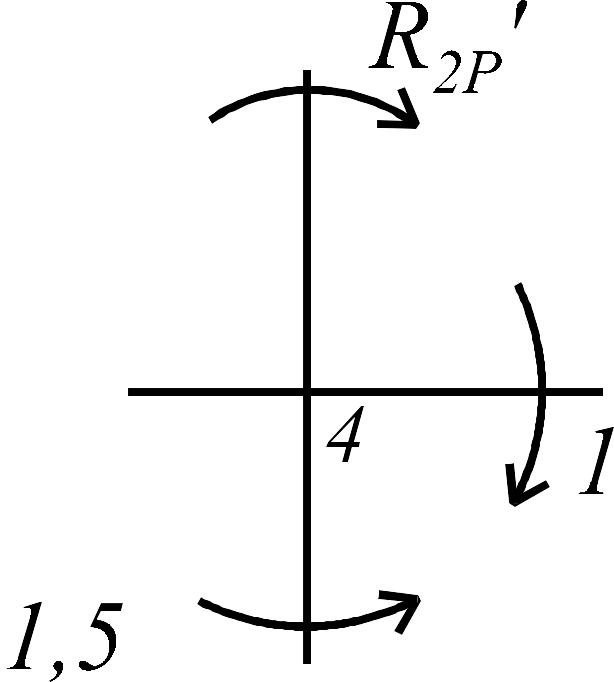
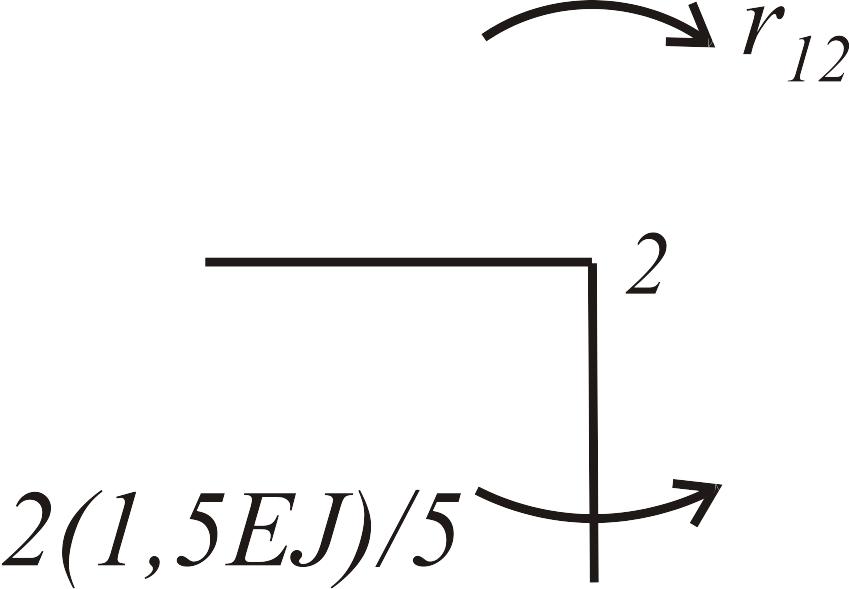
Состояние 2 (эпюра )
|
:
|
|
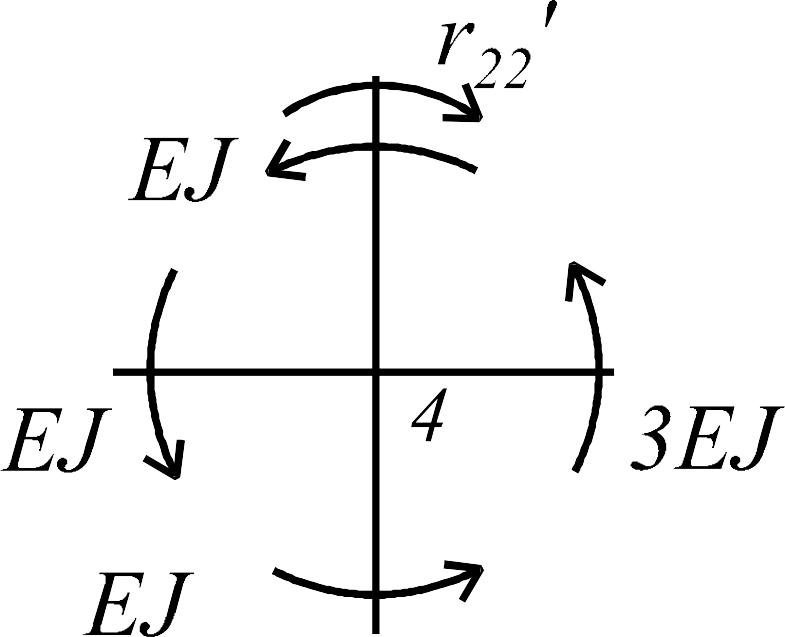
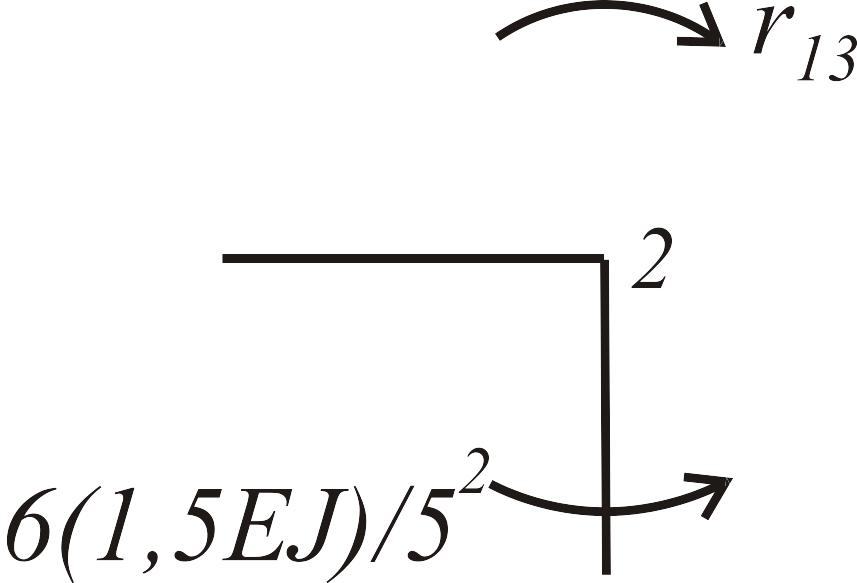
Состояние 3 (эпюра )
|
:
|
|
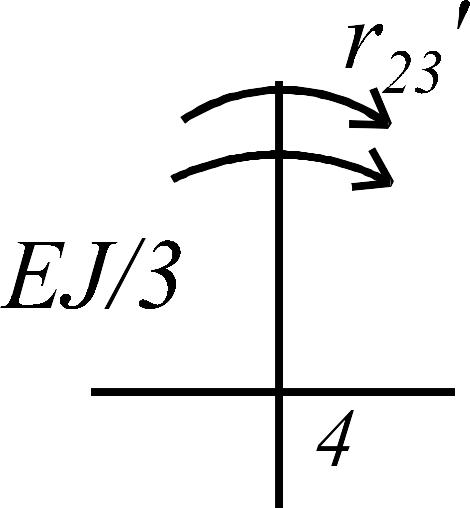
Состояние 1 (эпюра )
|
|
|
Состояние 2 (эпюра )
|
:
|
|
Состояние 3 (эпюра )
|
:
|
|