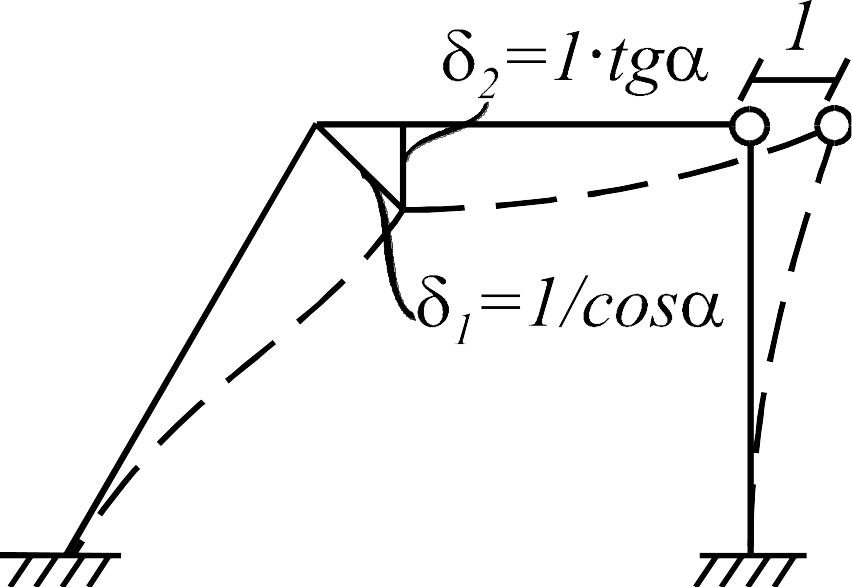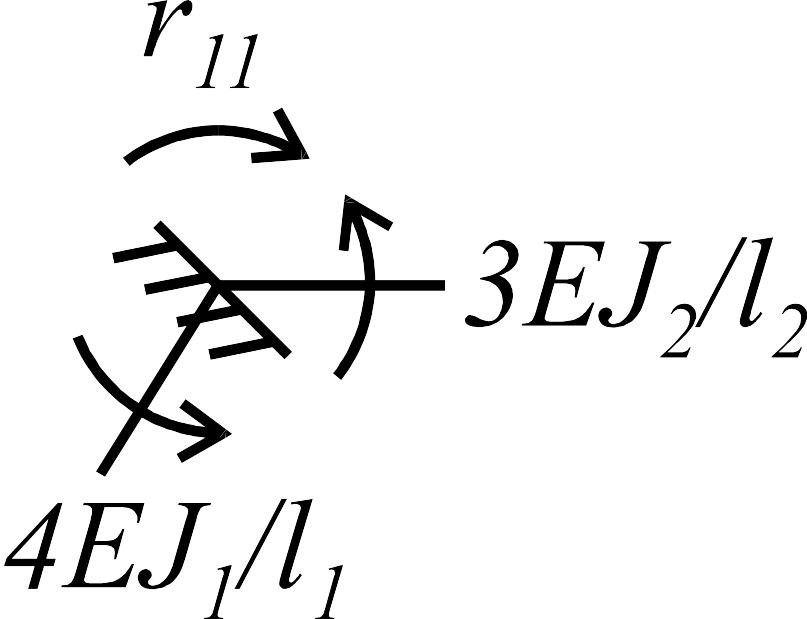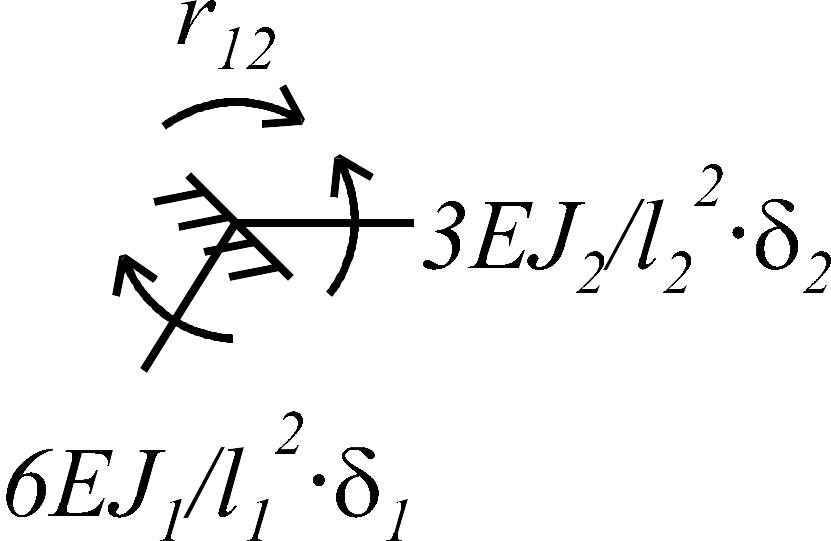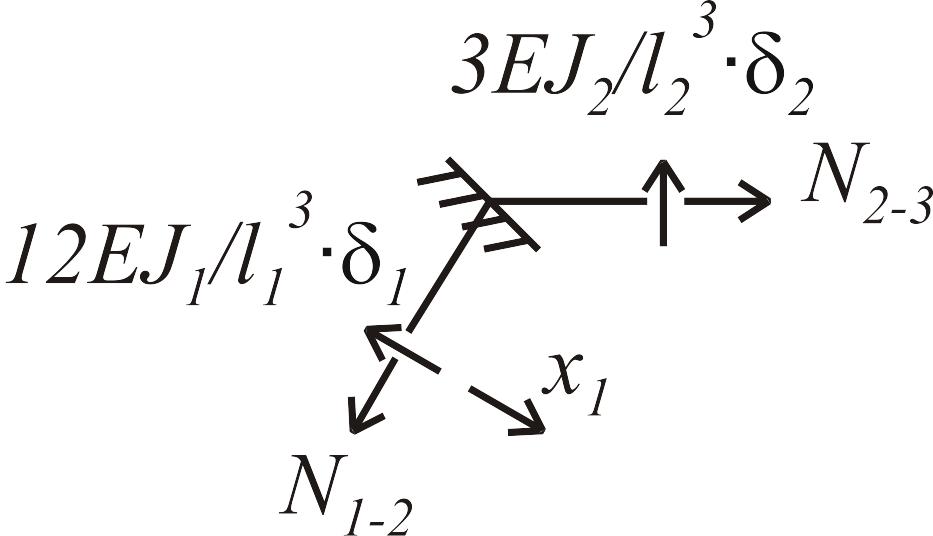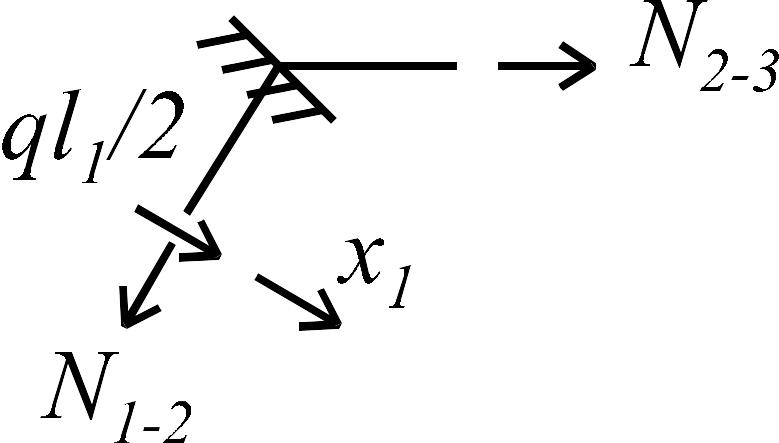- •13. Расчет статически неопределимых стержневых систем методом перемещений, смешанным и комбинированным методами
- •1. Основные положения методов перемещений, смешанного и комбинированного
- •1.1. Расчет статически неопределимых систем методом перемещений
- •1.1.1. Выбор неизвестных и основной системы
- •1.1.2. Система разрешающих уравнений в канонической форме
- •1.1.3. Вычисление коэффициентов системы канонических уравнений
- •1.1.4. Построение действительных эпюр внутренних усилий
- •1.1.5. Проверки расчетов
- •1.2. Особенности расчета симметричных рам
- •1.3. Особенности расчета статически неопределимых рам с наклонными стойками
- •1.4. Учет упругой податливости опор при расчете стержневых систем
- •1.5. Смешанный и комбинированный методы расчета статически неопределимых систем
- •Продолжение табл. 4
- •Окончание табл. 4
- •Окончание табл. 5
1.3. Особенности расчета статически неопределимых рам с наклонными стойками
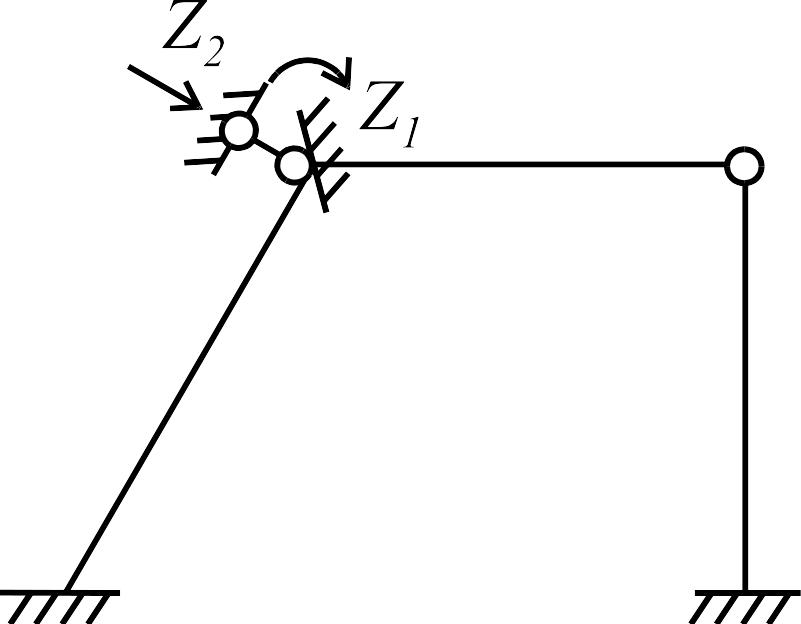
Наличие в статически неопределимых рамах наклонных (неортогонально соединенных) элементов приводит к заметному усложнению их расчета методом перемещений. Покажем это на примере рамы, изображенной на рис. 1.6 а. Выберем для нее основную систему метода перемещений, построим единичные и грузовую эпюры и определим коэффициенты канонических уравнений.
а |
б |
в |
|
|
|
Рис. 1.6
Примем основную систему метода перемещений, показанную на рис. 1.6 б, в. При этом дополнительную линейную связь можно поставить по-разному: либо перпендикулярно наклонному стержню (рис. 1.6 б), либо вдоль горизонтального элемента (рис. 1.6 в). В обоих случаях будут устранены линейные перемещения узлов рамы.
Единичная
(рис. 1.7 а) и грузовая
(рис. 1.7 д) эпюры строятся без каких-либо
осложнений с использованием табличных
решений. При этом из равновесия узла 2
определяются коэффициенты
![]() ,
(рис. 1.8 а, д):
,
(рис. 1.8 а, д):
![]() ;
;
![]() .
.
а |
|
б |
|
в |
|
||||
г |
|
д |
|
|
|||||
Рис. 1.7
а |
|
б |
|
в |
|
г |
|
д |
|
е |
|
ж |
|
з |
|
и |
|
Рис. 1.8
Сложности
появляются при построении эпюры
от линейного единичного смещения узла
3
![]() (при этом возникает эпюра моментов в
горизонтальном элементе 2-3). Предварительно
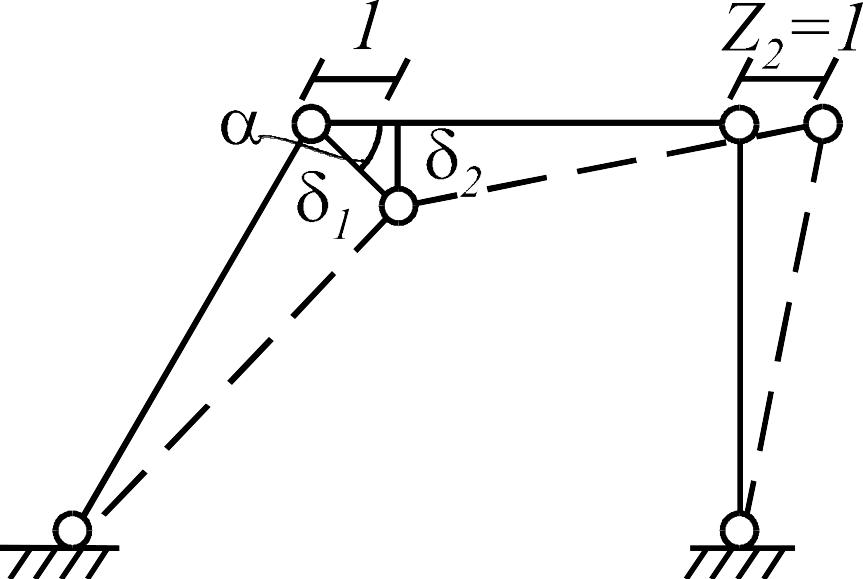
нужно построить план перемещений
шарнирно-стержневой схемы рамы (рис.
1.7 б). Все составляющие перемещений
узлов, необходимые для построения эпюры
,
приведены на рис. 1.7 в. При этом возникает
взаимное поперечное смещение концов
наклонного элемента и ригеля
(при этом возникает эпюра моментов в
горизонтальном элементе 2-3). Предварительно
нужно построить план перемещений
шарнирно-стержневой схемы рамы (рис.
1.7 б). Все составляющие перемещений
узлов, необходимые для построения эпюры
,
приведены на рис. 1.7 в. При этом возникает
взаимное поперечное смещение концов
наклонного элемента и ригеля
![]() и
и
![]() .
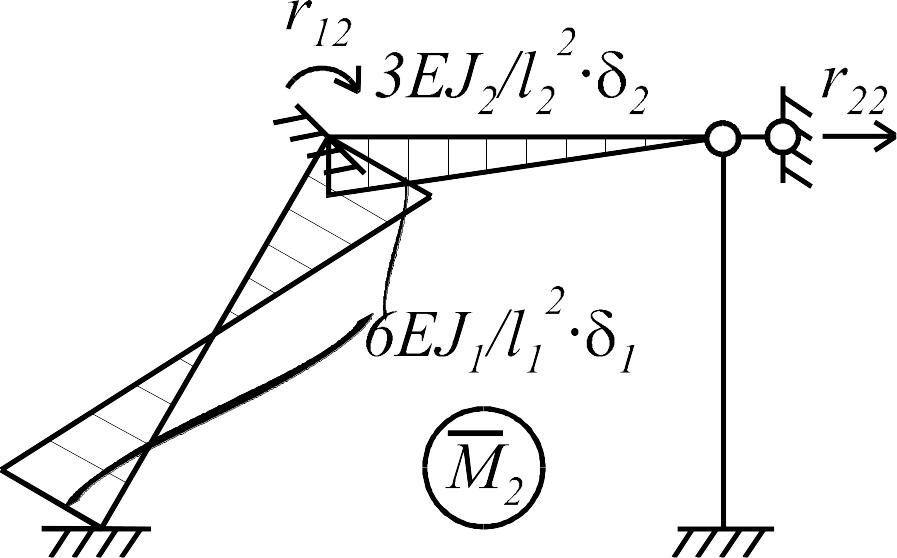
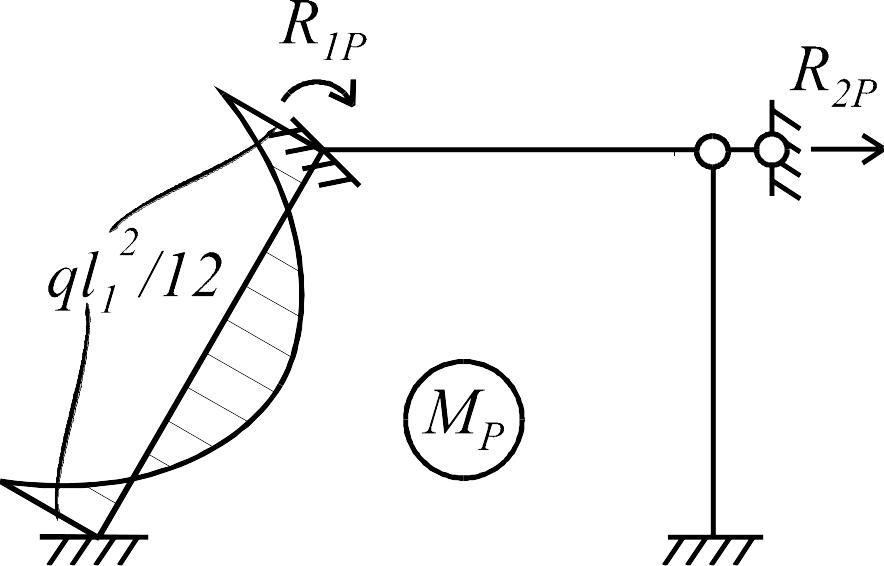
По данной эпюре (рис. 1.7 г) из условия
равновесия узла 1 (рис. 1.8 б) определим
коэффициент
.
По данной эпюре (рис. 1.7 г) из условия
равновесия узла 1 (рис. 1.8 б) определим
коэффициент
![]() :
:
![]() .
.
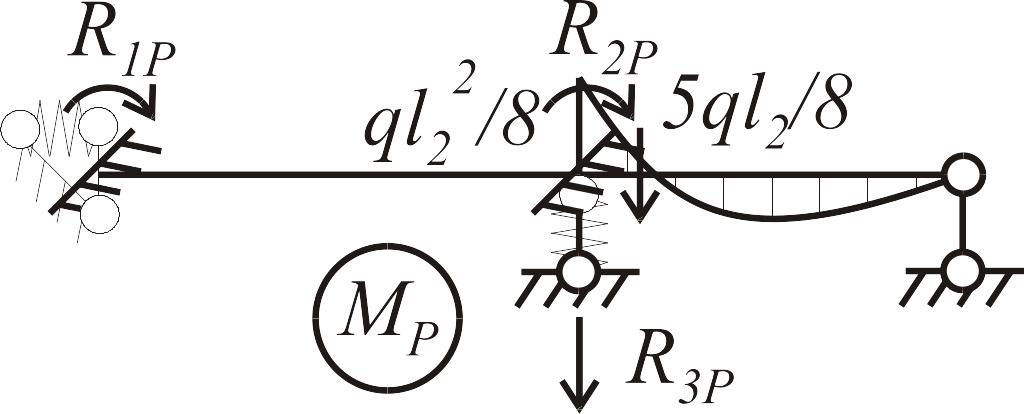
Отметим
еще одну особенность, которая возникает
при определении реакций в дополнительной
линейной связи в узле 3 (коэффициентов
![]() ,
,
![]() и
и
![]() ),
исходя из условия
),
исходя из условия
![]() .
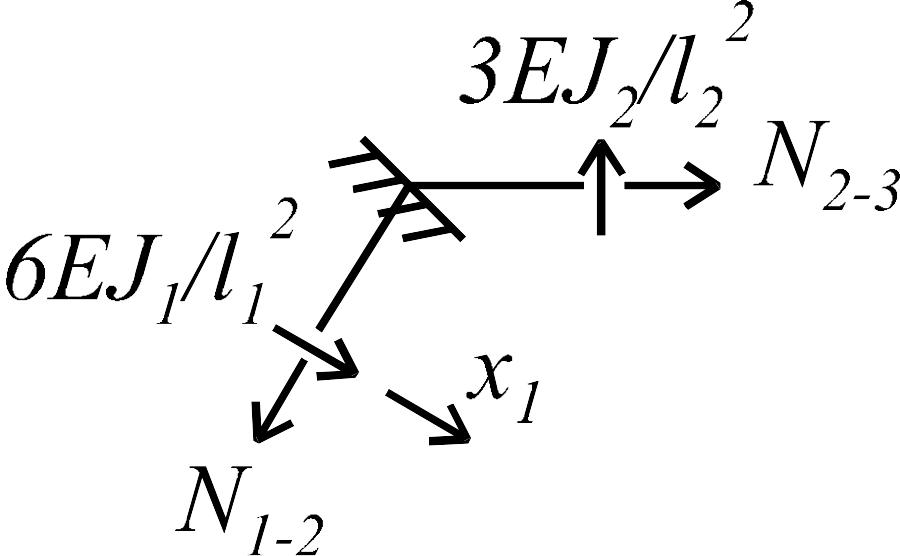
В это уравнение, кроме значений известных
поперечных сил и искомой реакции, входят
значения продольных сил в наклонном
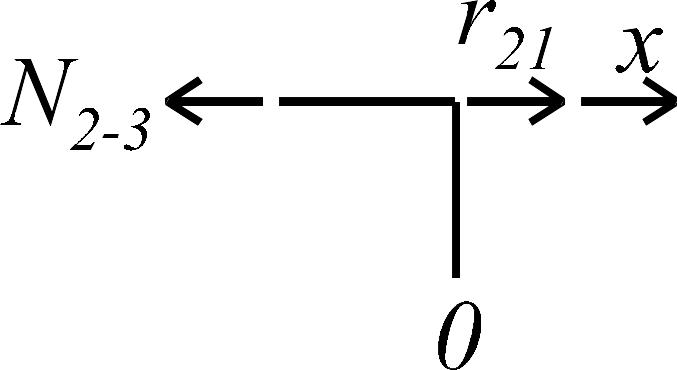
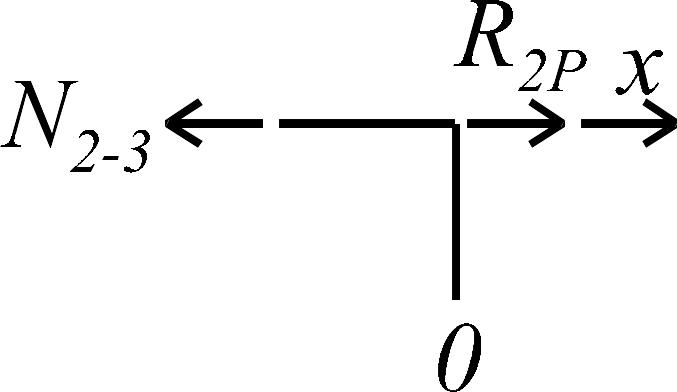
элементе. Для их определения вырежем
левый узел рамы, а затем из условий
равновесия правого узла найдем искомые
коэффициенты (рис. 1.8 г-и):
.
В это уравнение, кроме значений известных
поперечных сил и искомой реакции, входят
значения продольных сил в наклонном
элементе. Для их определения вырежем
левый узел рамы, а затем из условий
равновесия правого узла найдем искомые
коэффициенты (рис. 1.8 г-и):
 :
:
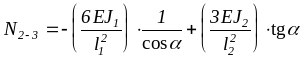 ;
;
![]() ;
;
 ;
;
 :
:
 ;
;
;
 ;
;
![]() :
:
![]() ;
;
![]() .
.
1.4. Учет упругой податливости опор при расчете стержневых систем
Опорные устройства реальных сооружений и конструкций обладают определенной податливостью, которую нередко приходится учитывать при составлении их расчетных схем.
Упруго-податливой связью (упруго смещающейся опорой) считают такую связь, перемещение которой пропорционально действующей на нее нагрузке (реакции). Упругими характеристиками таких опор являются коэффициенты податливости или жесткости, которые должны быть заданы заранее.
а
б
Рис. 1.9
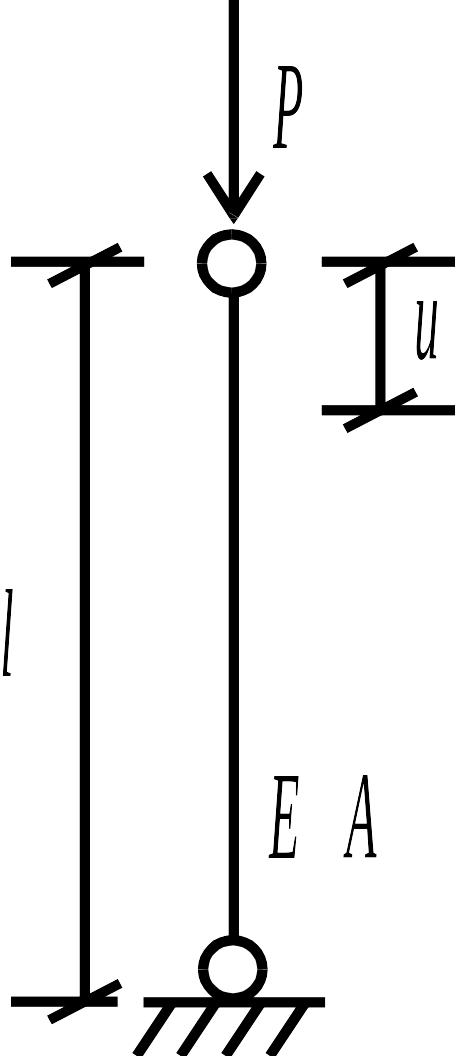
![]() и с поперечным сечением
и с поперечным сечением
![]() (укорочение
(укорочение
![]() ),
является число
),
является число
![]() .
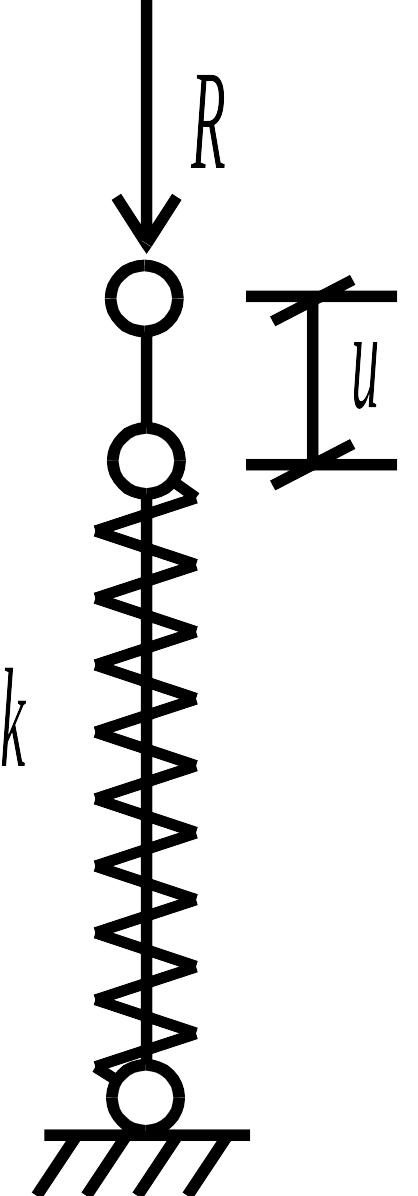
Коэффициентом жесткости
.
Коэффициентом жесткости
![]() (жесткостью опоры) называется величина,
обратная податливости, то есть
(жесткостью опоры) называется величина,
обратная податливости, то есть
![]() (рис. 1.9 б). При этом
(рис. 1.9 б). При этом
![]() ,
а величины
и
,
а величины
и
![]() подбирают так, чтобы
подбирают так, чтобы
![]() .
Коэффициент жесткости представляет
собой величину силы, необходимой для
единичного смещения опоры.
.
Коэффициент жесткости представляет
собой величину силы, необходимой для
единичного смещения опоры.
В
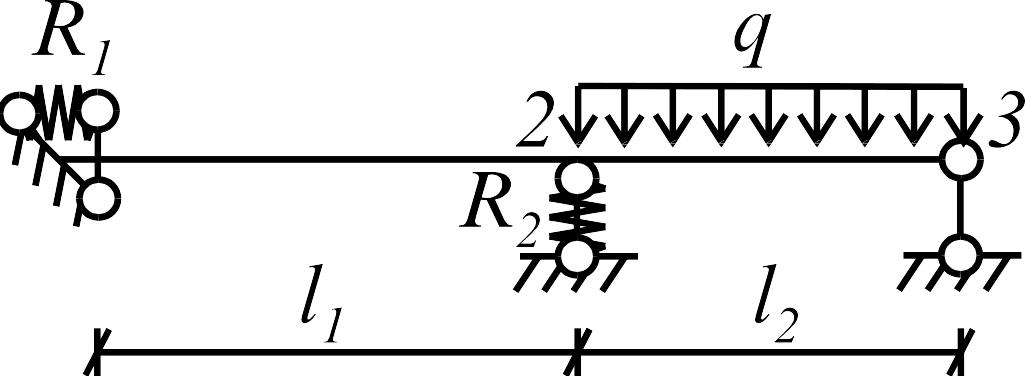
качестве примера системы, в которой
учитывается упругая податливость
опорных связей, рассмотрим неразрезную
балку (рис. 1.10 а). Ее левая опора представляет
собой заделку, упруго сопротивляющуюся
повороту (упругая моментная связь), а
промежуточная опора - сосредоточенную
упругую опору в виде пружины. Коэффициенты
жесткости опор
![]() ,
,
![]() считаем заданными.
считаем заданными.
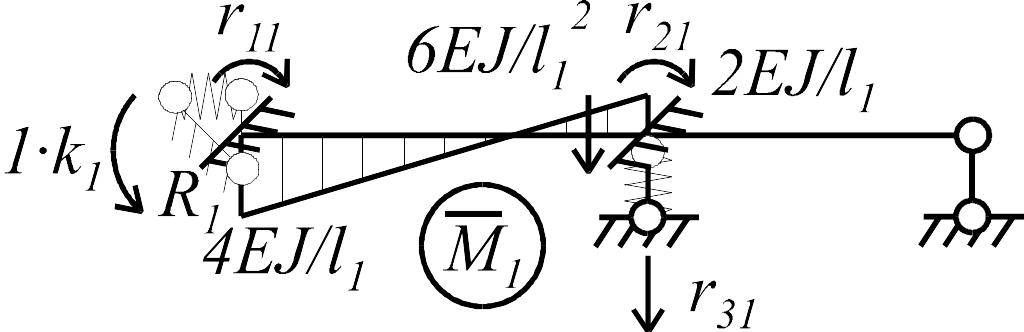
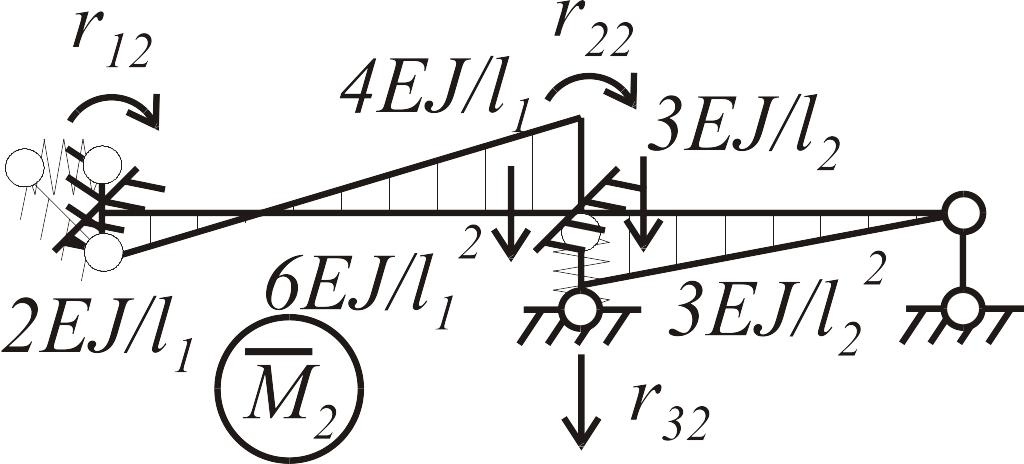
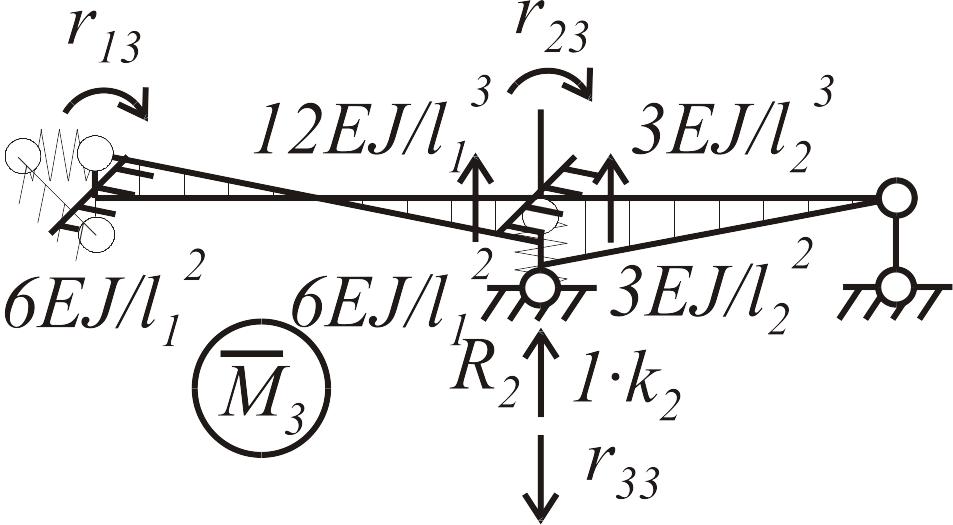
Основная система, используемая при расчете балки методом перемещений, показана на рис. 1.10 б. Неизвестными являются углы поворота поперечных сечений балки в точках 1 и 2, а также линейное вертикальное перемещение опоры 2. Единичные и грузовая эпюры приведены на рис. 1.10 в-е.
При
вычислении коэффициентов
и
![]() в их выражения войдут коэффициенты
жесткости заделки
и промежуточной опоры
соответственно как реакции, возникающие
в упругих моментной и линейной связях
от
и
в их выражения войдут коэффициенты
жесткости заделки
и промежуточной опоры
соответственно как реакции, возникающие
в упругих моментной и линейной связях
от
и
![]() :
:
![]() ;
;
![]() .
.
а |
|
б |
|
в |
|
г |
|
д |
|
е |
|
Рис. 1.10
В дальнейшем расчет балки идет согласно обычному алгоритму метода перемещений.