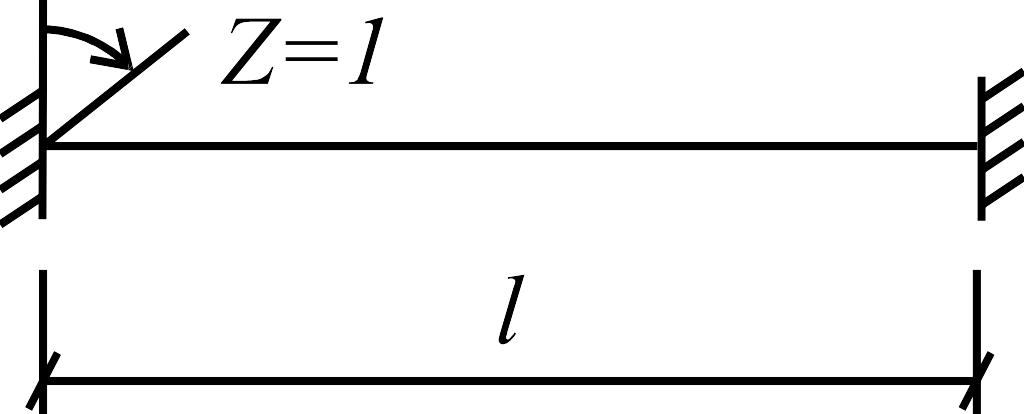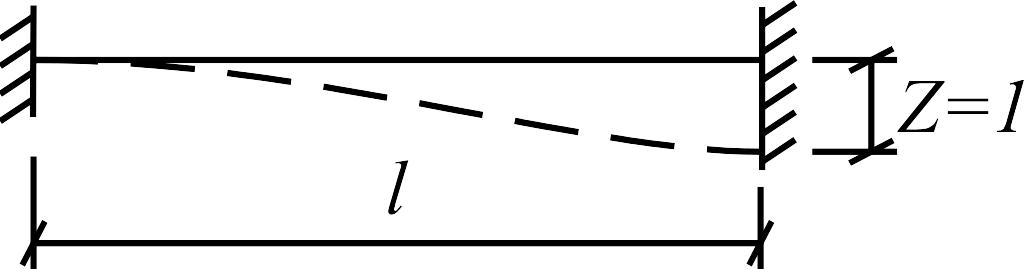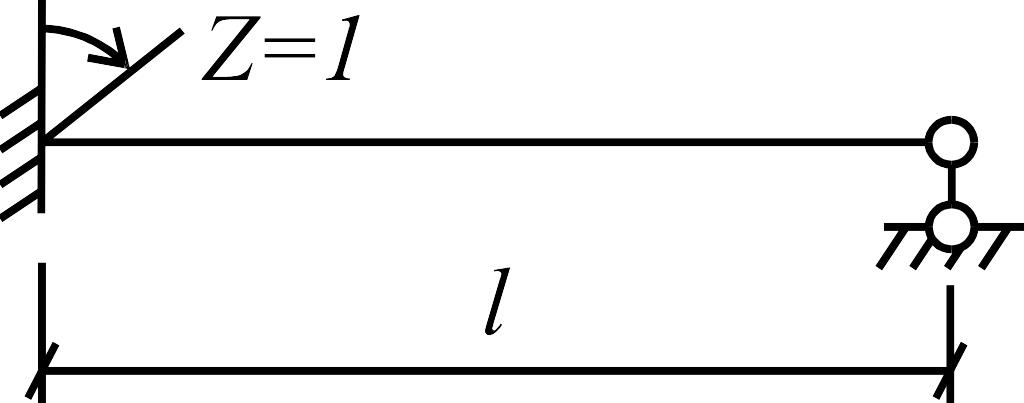1.1.2. Система разрешающих уравнений в канонической форме

Как видно из рассмотренного примера, основная система метода перемещений эквивалентна заданной схеме рамы по распределению внутренних усилий, деформаций и перемещений при условии равенства нулю реакций в дополнительно введенных связях, так как в заданной системе эти связи отсутствуют. Это обстоятельство используется для составления системы разрешающих уравнений:

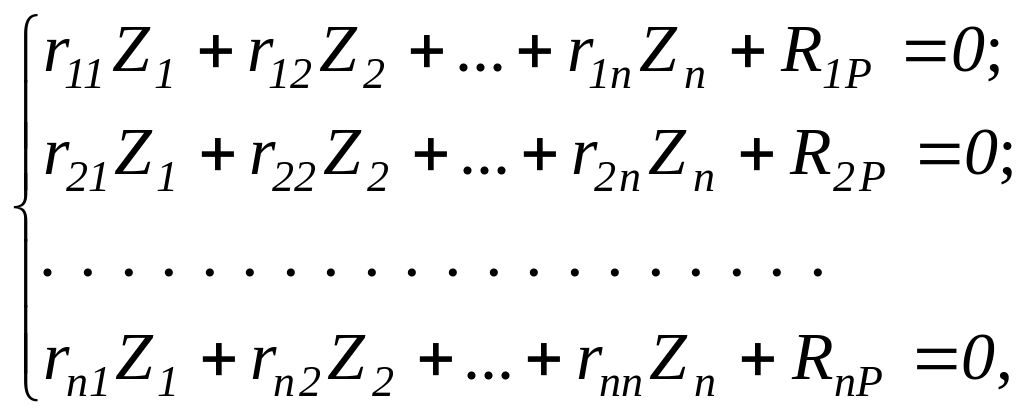(1.3)

где - реакция (реактивный момент или реактивная сила) в -й ( ) дополнительной связи основной системы, вызванная единичным перемещением -й связи ( ); - реакция в -й дополнительной связи в результате действия внешней нагрузки.

Для определения коэффициентов при неизвестных и свободных членов системы канонических уравнений необходимо предварительно построить в основной системе метода перемещений эпюры изгибающих моментов от единичных значений неизвестных перемещений , , ..., и от внешней нагрузки. При этом используются табличные решения (табл. 1).

Поскольку основная система представляет собой совокупность отделенных друг от друга защемлениями или шарнирами элементов (однопролетных статически неопределимых балок), то построение единичных и грузовой эпюр , , ..., , не вызывает затруднений. Единичное состояние любого элемента связано только с единичными перемещениями его концов и не зависит от состояния остальных элементов.

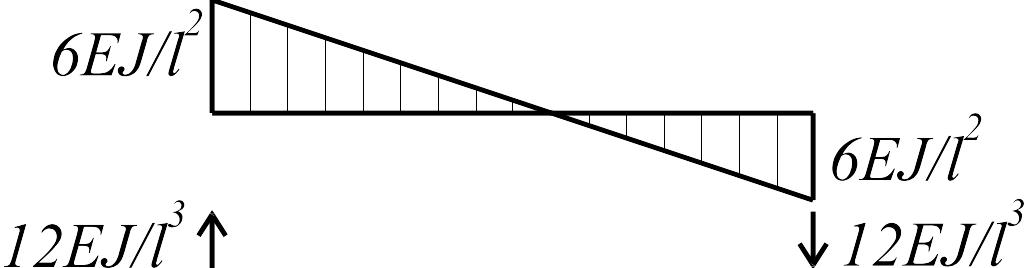
Таблица 1

Эпюра моментов и реакции	Эпюра моментов и реакции

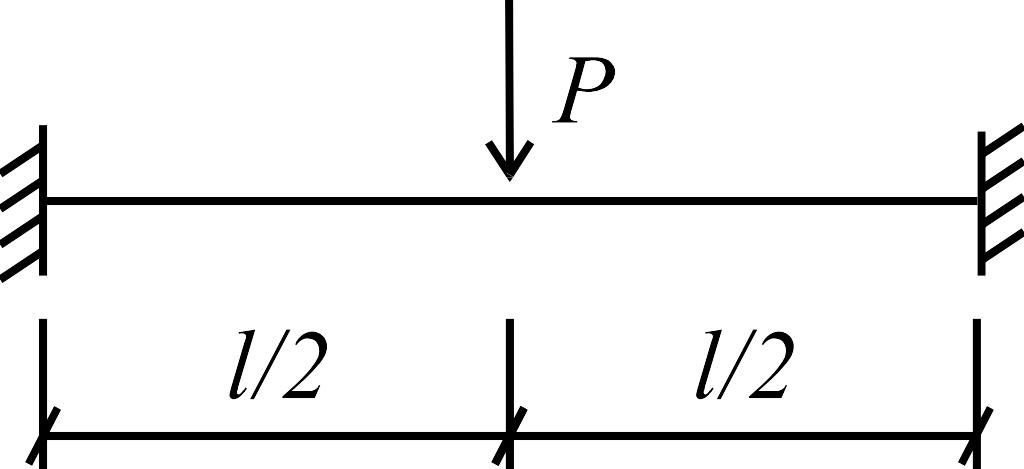
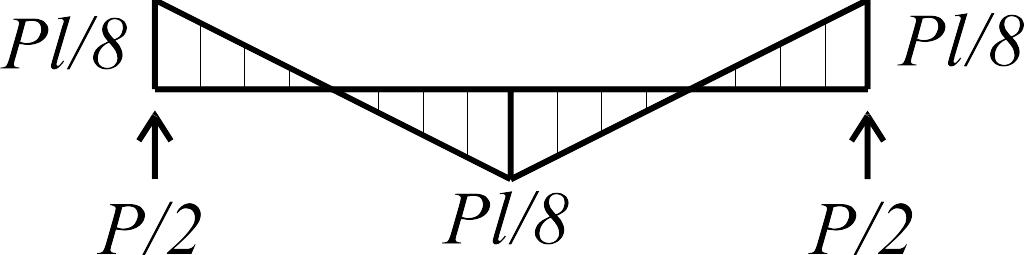
Эпюры , , ..., могут быть построены с помощью решений, приведенных в табл. 1, от действия единичного угла поворота заделки и единичного смещения опор . Для составления таблиц (построения эпюр моментов и определения реакций) в статически неопределимых стержнях использовался метод сил.

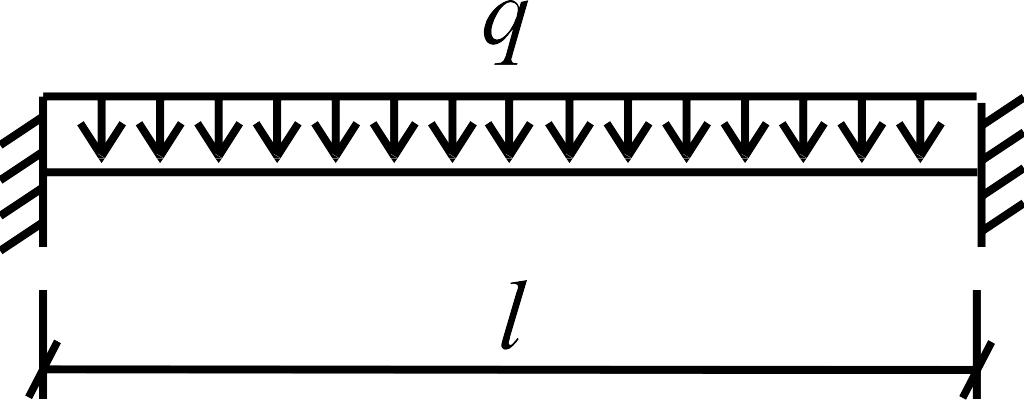
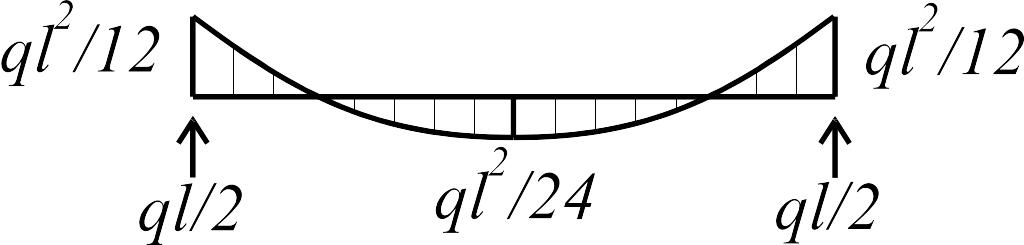
Грузовые эпюры от действия различных внешних нагрузок в основной системе строятся столь же просто, с применением решений, приведенных в табл. 1.

Для балки с шарнирными опорами на концах решения легко находятся при любом загружении с помощью только уравнений равновесия и поэтому в таблицах не приводятся. В силу принятых допущений решения, данные в табл. 1, справедливы и для балок, имеющих в шарнирной опоре горизонтальную связь.

1.1.3. Вычисление коэффициентов системы канонических уравнений

Единичные и грузовые коэффициенты (реакции в дополнительных связях) , определяются статическим способом. При этом реактивные моменты в упругих защемлениях находятся из условий равновесия узлов рамы, а реакции в дополнительных опорных стержнях – из условия равновесия частей рамы, отсеченных от опорных закреплений.

Направление реактивного усилия считается положительным, если оно совпадает с направлением перемещения, заданного при построении единичной эпюры.

В ходе решения системы канонических уравнений определяют величины углов поворота и линейных смещений узлов заданной рамы, что позволяет построить действительные эпюры внутренних усилий в статически неопределимой раме.