- •13. Расчет статически неопределимых стержневых систем методом перемещений, смешанным и комбинированным методами
- •1. Основные положения методов перемещений, смешанного и комбинированного
- •1.1. Расчет статически неопределимых систем методом перемещений
- •1.1.1. Выбор неизвестных и основной системы
- •1.1.2. Система разрешающих уравнений в канонической форме
- •1.1.3. Вычисление коэффициентов системы канонических уравнений
- •1.1.4. Построение действительных эпюр внутренних усилий
- •1.1.5. Проверки расчетов
- •1.2. Особенности расчета симметричных рам
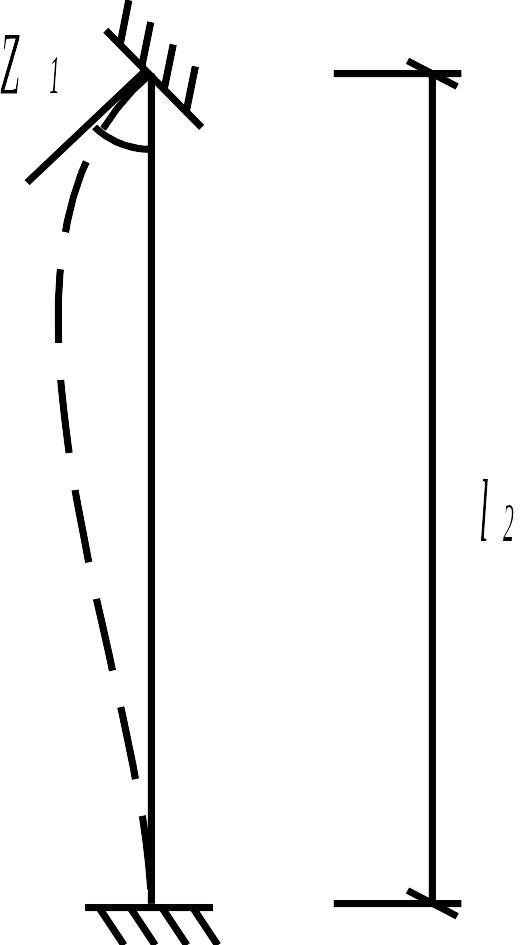
- •1.3. Особенности расчета статически неопределимых рам с наклонными стойками
- •1.4. Учет упругой податливости опор при расчете стержневых систем
- •1.5. Смешанный и комбинированный методы расчета статически неопределимых систем
- •Продолжение табл. 4
- •Окончание табл. 4
- •Окончание табл. 5
13. Расчет статически неопределимых стержневых систем методом перемещений, смешанным и комбинированным методами
Как известно, для определения усилий в статически определимых системах недостаточно одних уравнений статики, их необходимо рассматривать вместе с физическими и геометрическими уравнениями, выражающими условия деформации системы. Чтобы не решать совместно полную систему уравнений расчет, например, методом сил основывался на выделении из заданной системы статически определимой основной системы, расчет которой являлся достаточно простым. В этом случае, решение полной системы уравнений расчленялось на решении отдельно уравнений, являющимися условиями совместности деформаций с основными неизвестными – усилиями в лишних связях, и дальнейшим решением уравнений равновесия в статически определимой основной системе, из которых определялись остальные неизвестные (опорные реакции и внутренние усилия).
Расчет статически неопределимых систем в ряде случаев значительно упрощается, если за неизвестные принимать не усилия в лишних связях, а характерные перемещения – угловые и линейные перемещения узлов системы.
Статически неопределимые системы можно рассчитывать различными методами. Выбор самого рационального из них, т.е. требующего наименьших трудозатрат, является важным этапом для выполнения «ручного» счета.
В данных методических указаниях кратко излагаются теоретические основы расчета на действие статической нагрузки методами перемещений, смешанным и комбинированным. Приводятся примеры расчета плоских стержневых систем.
Работа предназначена студентам строительных и дорожно-строительных специальностей заочной формы обучения. Она может быть также использована как руководство к практическим занятиям и расчетно-проектировочным заданиям по курсу «Строительная механика» для студентов очной формы обучения.
1. Основные положения методов перемещений, смешанного и комбинированного
Метод перемещений является одним из наиболее распространенных методов расчета статически неопределимых систем и имеет свои преимущества.
Во многих случаях его применение приводит к снижению трудоемкости вычислительных работ. В логическом отношении данный метод проще метода сил, хорошо алгоритмизируется и поэтому является более предпочтительным и эффективным при использовании ЭВМ.
Трудоемкость метода перемещений (в частности, число его неизвестных) зависит от допущений. Обычно в целях упрощения, особенно при «ручном» счете, пренебрегают продольными деформациями стержней и деформациями сдвига, а также сближением концов стержней при изгибе.
1.1. Расчет статически неопределимых систем методом перемещений
1.1.1. Выбор неизвестных и основной системы
При расчете рам в качестве неизвестных принимаются перемещения узлов рамы, которые подразделяются на угловые и линейные. Узлами рамы следует считать места жесткого или шарнирного соединения стержней, точки излома оси стержня, места скачкообразного изменения жесткости стержня.
Общее
число неизвестных
![]() складывается из угловых перемещений
складывается из угловых перемещений
![]() (поворотов жестких узлов) и линейных
перемещений
(поворотов жестких узлов) и линейных
перемещений
![]() как жестких, так и шарнирных узлов. Число
угловых неизвестных
равно числу жестких узлов. Для подсчета
числа линейных неизвестных
необходимо заданную раму путем введения
сквозных шарниров во все узлы, включая
опорные, преобразовать в шарнирно-стержневую
систему, степень подвижности которой
определяется по формуле
как жестких, так и шарнирных узлов. Число
угловых неизвестных
равно числу жестких узлов. Для подсчета
числа линейных неизвестных
необходимо заданную раму путем введения
сквозных шарниров во все узлы, включая
опорные, преобразовать в шарнирно-стержневую
систему, степень подвижности которой
определяется по формуле
![]() ,
(1.1)
,
(1.1)
где
![]() - число шарнирных узлов (в шарнирно-стержневой
схеме все узлы шарнирные);
- число шарнирных узлов (в шарнирно-стержневой
схеме все узлы шарнирные);
![]() - число стержней, соединяющих узлы;
- число стержней, соединяющих узлы;
![]() - число опорных связей. В расчетах можно
использовать и формулу
- число опорных связей. В расчетах можно
использовать и формулу
![]() .
(1.2)
.
(1.2)
Число линейных перемещений узлов определяется количеством дополнительных стержней, которые нужно ввести в шарнирную схему рамы, для того чтобы превратить ее в геометрически неизменяемую. При соответствующем опыте это легко можно выяснить при визуальном анализе возможных перемещений элементов шарнирной схемы.
Количество неизвестных метода перемещений называют степенью кинематической неопределимости рамы.
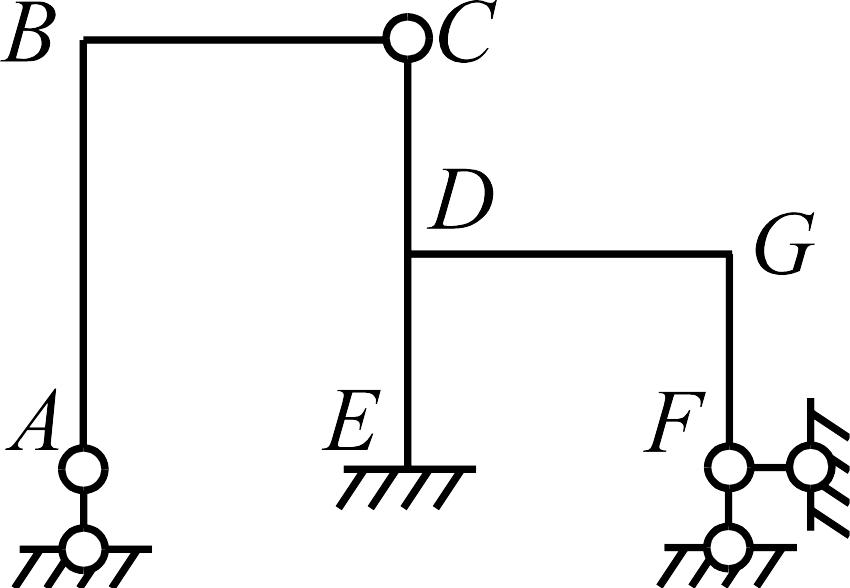
Найдем число неизвестных метода перемещений для рамы (рис. 1.1 а).
а |
|
б |
|
в |
|
г |
|
Рис. 1.1
Число
неизвестных угловых перемещений равно
трем (углы поворота жестких узлов
![]() ,
,
![]() ,
,
![]() ).
Для определения числа линейных перемещений
узлов
образуем шарнирную схему, т.е. поставим
шарниры во все узлы рамы (рис. 1.1 б).
).
Для определения числа линейных перемещений
узлов
образуем шарнирную схему, т.е. поставим
шарниры во все узлы рамы (рис. 1.1 б).
При
этом
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
В
случае использования формулы (1.2)
![]() ,
,
![]() (в узле
шарнир двойной, а остальные одинарные),
.
Поэтому
(в узле
шарнир двойной, а остальные одинарные),
.
Поэтому
![]()
![]() .
.
Все
шесть неизвестных показаны на рис. 1.1 в
штриховыми линиями. Анализируя возможные
перемещения узлов рамы, видим, что узлы
![]() ,
,
![]() ,
могут перемещаться только по горизонтали,
а вертикальные перемещения узлов
,
,
,
невозможны вследствие принятого
допущения о нерастяжимости стержней и
закрепления в узлах
,
,
могут перемещаться только по горизонтали,
а вертикальные перемещения узлов
,
,
,
невозможны вследствие принятого
допущения о нерастяжимости стержней и
закрепления в узлах
,
![]() ,
,
![]() .
.
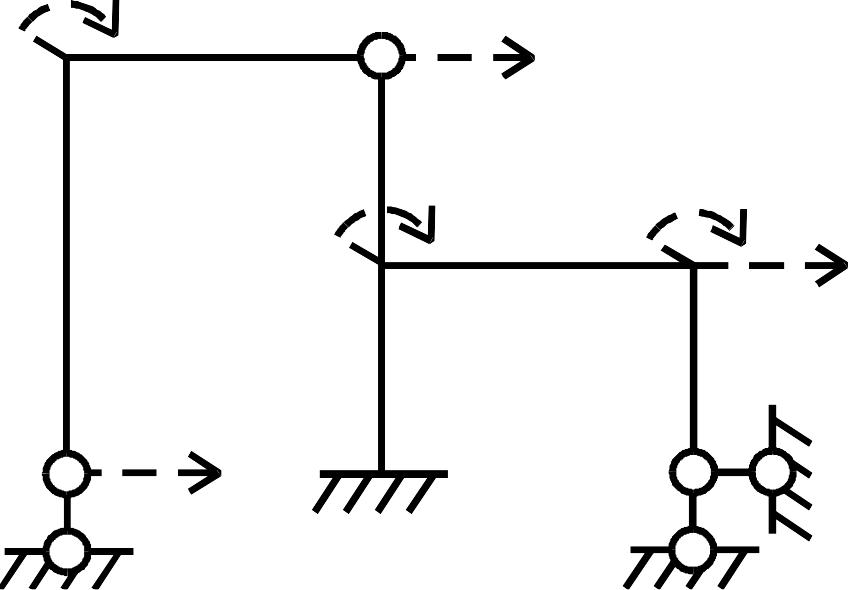
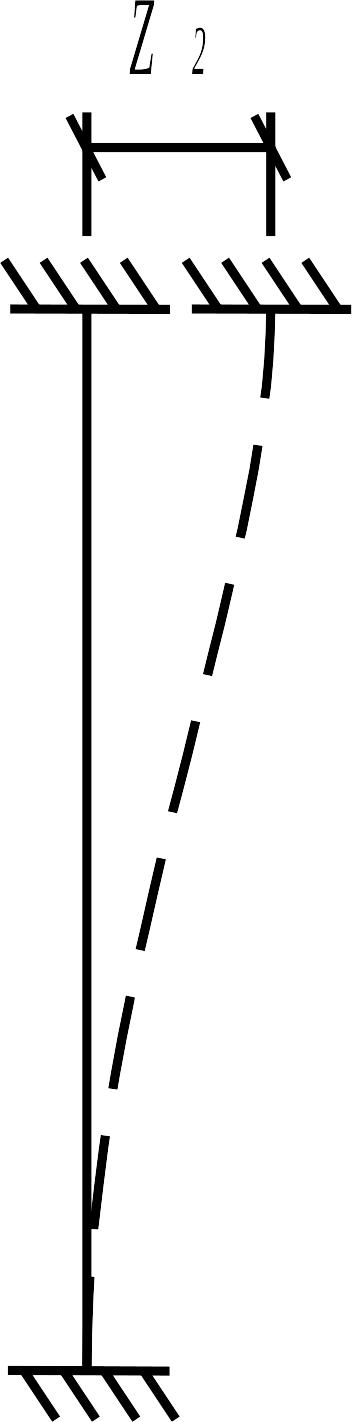
Расчет статически неопределимой рамы методом перемещений, как и методом сил, выполняется в основной системе, образуемой из заданной (однако не путем устранения, а путем наложения дополнительных связей, которые бы полностью исключили возможность перемещений всех узлов рамы, рис. 1.1 г). Основную идею метода перемещений поясним на примере рамы, приведенной на рис. 1.2 а.
а |
|
б |
|
|
|||||||||
в |
|
|
г |
|
|
||||||||
д |
|
|
е |
|
|
ж |
|
|
|||||
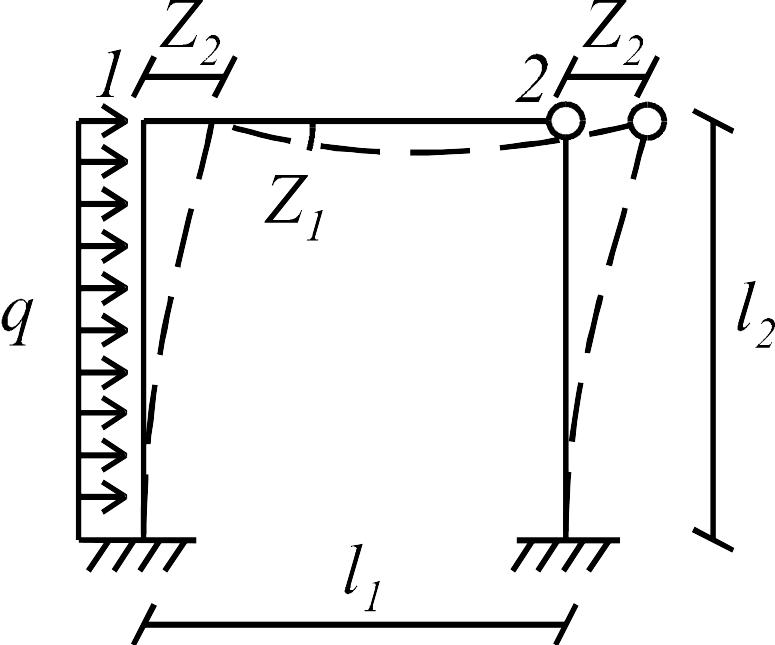
Рис. 1.2
От
действия на раму заданной нагрузки
![]() она деформируется. При этом узел 1
повернется на угол
она деформируется. При этом узел 1
повернется на угол
![]() и сместится вправо на величину
и сместится вправо на величину
![]() .
Ввиду малости деформаций расстояние
между узлами 1 и 2 после деформирования
можно считать таким же, как и до него,
поэтому узел 2 сместится вправо на ту
же величину
,
что и узел 1. Основная система метода
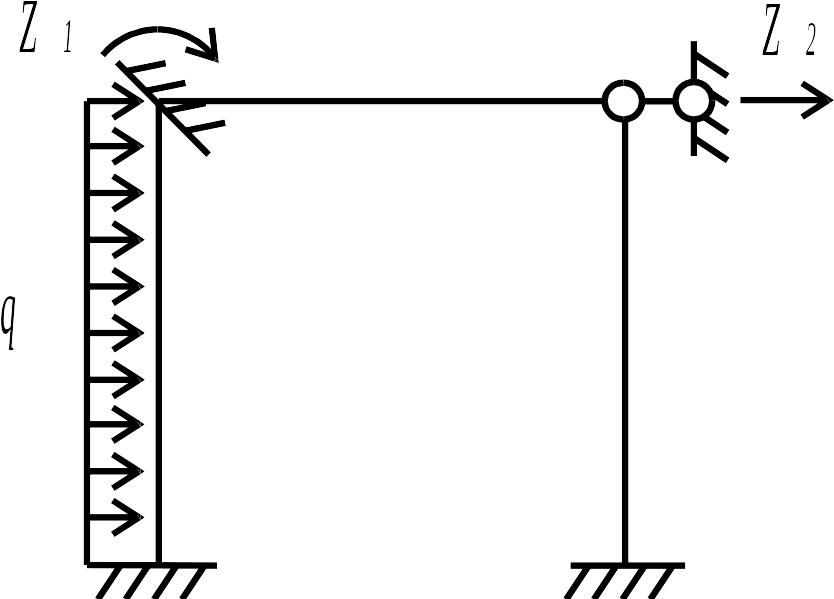
перемещений (рис. 1.2 б) получена из
заданной добавлением двух связей:
заделки в узле 1 и дополнительного
опорного стержня в узле 2. В результате
рама превратилась в набор однопролетных
статически неопределимых балок (стержней)
с неподвижными узлами.
.
Ввиду малости деформаций расстояние
между узлами 1 и 2 после деформирования
можно считать таким же, как и до него,
поэтому узел 2 сместится вправо на ту
же величину
,
что и узел 1. Основная система метода
перемещений (рис. 1.2 б) получена из
заданной добавлением двух связей:
заделки в узле 1 и дополнительного
опорного стержня в узле 2. В результате
рама превратилась в набор однопролетных
статически неопределимых балок (стержней)
с неподвижными узлами.
Следует отметить, что дополнительную связь, введенную в узел 1, называют подвижной заделкой: она препятствует повороту узла, но не мешает его линейному смещению. Рассмотрим деформацию каждого из стержней в основной системе рамы.
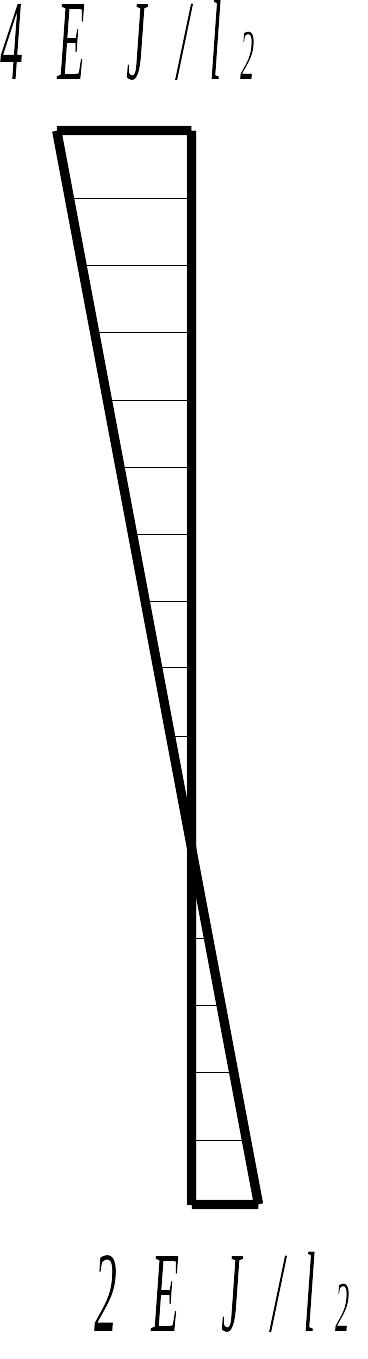
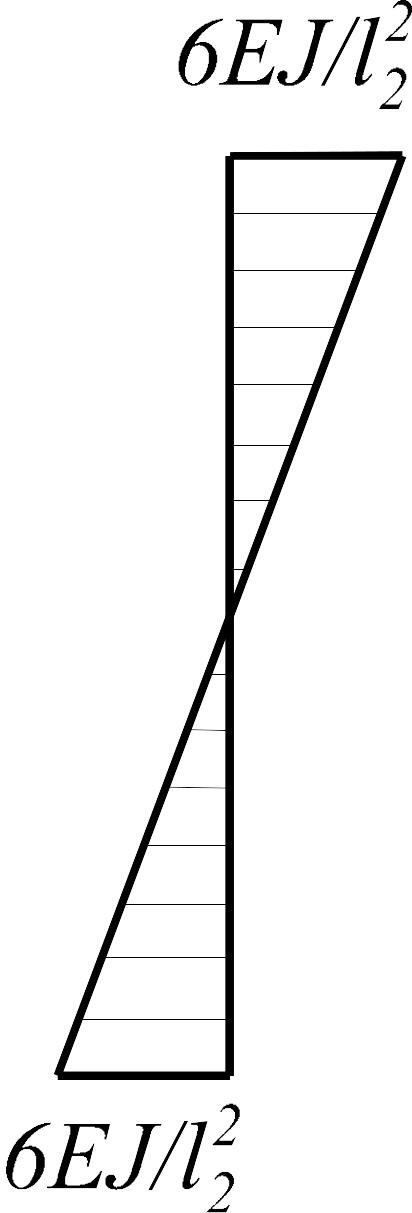
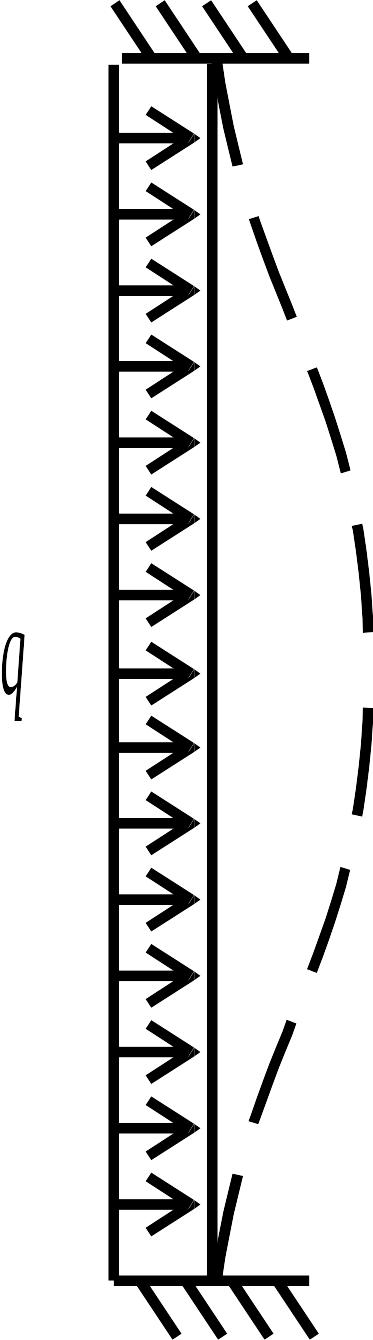
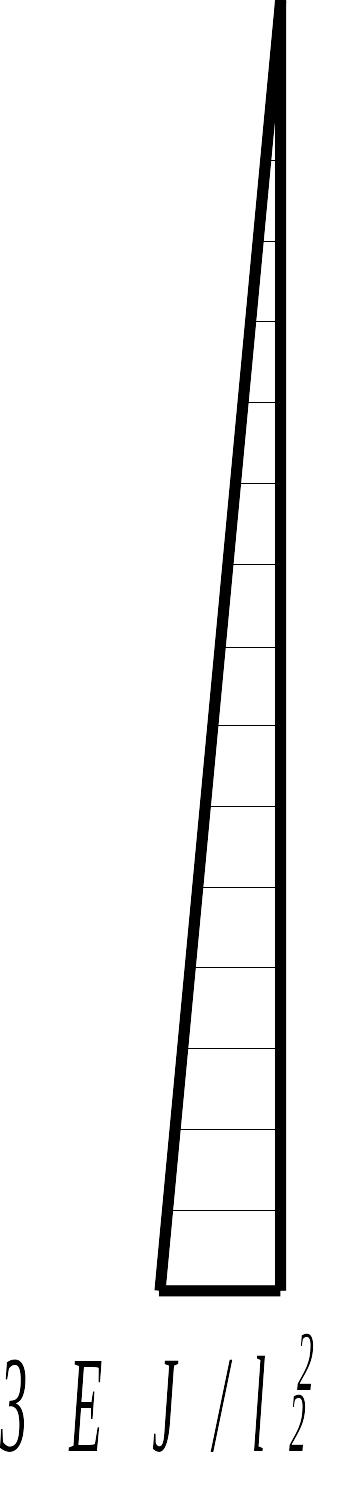
От поворота узла 1 на угол левая стойка и ригель деформируются независимо друг от друга, как показано на рис. 1.2 в, г. Левая стойка (балка с защемленными концами) изогнется при повороте левого сечения на угол ; ригель (балка, защемленная слева и шарнирно опертая справа) при повороте первого сечения повернется на тот же угол . При смещении узлов 1 и 2 на величину левая и правая стойки изогнутся так, как показано на рис. 1.2 д, ж соответственно. Кроме того, левая стойка деформируется также и от действия внешней нагрузки (рис. 1.2 е).
Если
найти угол поворота
и линейное перемещение
,
то можно построить эпюры изгибающих
моментов от этих воздействий и, сложив
их с эпюрой от внешней нагрузки на основе
принципа независимости действия сил,
получить суммарную (действительную)
эпюру, соответствующую деформации
заданной системы. Для определения
и
составляются разрешающие уравнения,
суть которых в следующем. Стержень рамы,
деформируясь в основной системе,
«стремится» повернуть дополнительную
связь (заделку), в результате чего в ней
возникают соответствующие реакции
(реактивные моменты)
![]() .
За положительное направление для
реактивных моментов примем направление
по часовой стрелке.
.
За положительное направление для
реактивных моментов примем направление
по часовой стрелке.
Аналогично
при деформации стержней рамы от
перемещения узлов 1 и 2 в дополнительной
опорной связи 2 возникает противодействующая
линейная реакция
![]() .
В этих выражениях первый индекс означает
номер дополнительной связи, в которой
возникает реакция, второй - причину
возникновения реакции. Например,
.
В этих выражениях первый индекс означает
номер дополнительной связи, в которой
возникает реакция, второй - причину
возникновения реакции. Например,
![]() - это реакция (реактивный момент) в
заделке 1 от линейного смещения рамы
;
- это реакция (реактивный момент) в
заделке 1 от линейного смещения рамы
;
![]() - линейная реакция в дополнительной
связи 2 от заданной нагрузки. Поскольку
в заданной системе этих дополнительных
связей нет, суммарные реакции, возникающие
в них, должны быть равны нулю, то есть
- линейная реакция в дополнительной
связи 2 от заданной нагрузки. Поскольку
в заданной системе этих дополнительных
связей нет, суммарные реакции, возникающие
в них, должны быть равны нулю, то есть
![]() и
и
![]() .
Используя принцип суперпозиции, выразим
слагаемые реакций
.
Используя принцип суперпозиции, выразим
слагаемые реакций
![]() и
и
![]() через реакции от единичных перемещений:
через реакции от единичных перемещений:
![]()
где
![]() - реакция в первой дополнительной связи
от ее поворота на угол
- реакция в первой дополнительной связи
от ее поворота на угол
![]() ;
;
![]() - реакция в этой же связи от смещения в
направлении второй связи
- реакция в этой же связи от смещения в
направлении второй связи
![]() и т.д. Полученные уравнения составляют
систему разрешающих уравнений метода
перемещений.
и т.д. Полученные уравнения составляют
систему разрешающих уравнений метода
перемещений.
В общем случае число дополнительных связей в основной системе равно . При этом в узлы рамы вводятся два типа связей: упругие защемления (заделки), которые препятствуют повороту жестких узлов и не лишают их линейной подвижности; дополнительные стержни, препятствующие только линейным смещениям. В первых возникают только реактивные моменты, а во вторых - реактивные силы, направленные вдоль стержней. Дополнительные связи должны быть введены таким образом, чтобы лишить узлы рамы возможности перемещаться. Поэтому упругие защемления устанавливаются во всех жестких узлах, а дополнительные стержни - по направлениям предполагаемых линейных смещений узлов, что превращает шарнирную схему рамы в геометрически неизменяемую.
Таким образом, основная система метода перемещений представляет собой набор статически неопределимых балок (см., например, рис. 1.1 г).