2.3. Уравнение касательной плоскости и нормали.
2.3.1. Касательная плоскость
к поверхности
в
точке
,
где
,
имеет уравнение
.
2.3.2. Нормаль к поверхности
в
точке
,
где
,
есть перпендикуляр в точке касания
.
Она имеет уравнение
.
Пример. Составить уравнение
касательной плоскости и нормали к
поверхности
в точке с координатами
.
Решение. Нам даны абсцисса
и
ордината
точки касания, найдем аппликату этой
точки:
.
Для составления искомых уравнений
потребуются значения частных производных
в точке касания
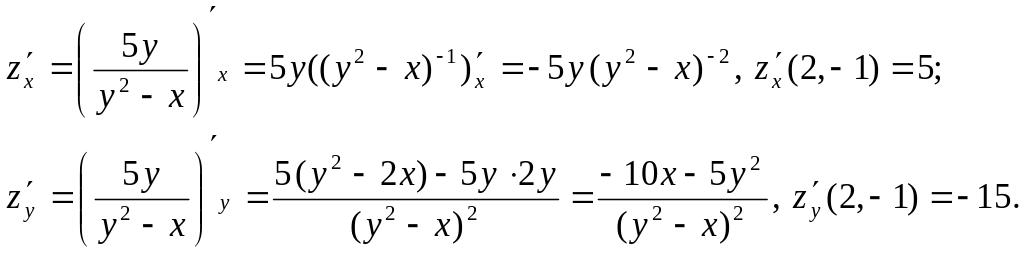
Теперь подставляем найденные значения в уравнение касательной плоскости:
или
.
Запишем также уравнение нормали:
.
Задачи для контрольной работы
Найти
уравнение касательной плоскости и
уравнение нормали к поверхности
в
точке
1.
. 14.
2.
. 15.
3.
. 16.
4.
17.
5.
18.
6.
19.
7.
20.
8.
21.
9.
22.
10.
23.
11.
24.
12.
25.
13.
2.4. Градиент и производная по направлению
2.4.1. Производная по направлению.
Рассмотрим вектор
,
соединяющий точки
и
координатной плоскости. Предел вида
естественно рассматривать как скорость
изменения функции в точке
в направлении вектора. Этот предел
называется производной функции
в точке
по направлению
.
Производную по направлению можно вычислить следующим образом:
=
,
где
направляющие косинусы вектора
.
2.4.2. Градиент. Вектор,
определяющий направление наискорейшего
возрастания функции
в точке
,
называется градиентом функции в этой
точке и обозначается
Градиент имеет следующие координаты:
,
}.
Пример.
Даны функция
и точка
.
Найти:
а) градиент данной функции в точке М;
б) производную этой функции в точке
по направлению вектора
,
где точка
- начало координат.
Решение.
Преобразуем данную функцию к виду
и найдем ее частные производные в точке
М:
,
.
Теперь
определяем градиент данной функции в
точке
.
Для нахождения производной данной
функции в точке М в направлении
вектора
найдем координаты вектора
,
его модуль
и его направляющие косинусы
,
.
Теперь подставляя в формулу для производной по направлению найденные величины и ранее вычисленные значения частных производных в точке М, имеем
.
Ответ:
,
Задачи для контрольной работы
Даны
функция
и
точка М. Найти:
а) градиент данной функции в точке М;
б) производную этой функции в точке по направлению вектора , где точка - начало координат.
1.
. 14.
2.
. 15.
3.
. 16.
4.
. 17.
5.
18.
6.
19.
7.
20.
8.
21.
9.
22.
10.
23.
11.
24.
12.
25.
13.
2.5. Экстремумы функций двух переменных. Наибольшее и наименьшее значения.
2.5.1. Экстремумы функций двух переменных.
Говорят, что функция
достигает
максимума (минимума) в точке
,
если ее значение
в указанной точке является наибольшим
(наименьшим) по сравнению со значениями
из
некоторой окрестности точки
.
Если функция
непрерывна в некоторой области
и обладает в
всеми непрерывными частными производными
до второго порядка включительно (эти
условия выполнены для всякой элементарной
функции двух переменных в ее области
определения), то поиск экстремумов
(максимумов и минимумов) может быть
осуществлен по такому алгоритму:
а) найти и ;
б) найти точки, в которых одновременно
и
(критические точки);
в) вычислив в каждой найденной критической
точке (
)
частные производные второго порядка
,
выяснить
знак выражения
.
Если
,
то в данной критической точке (
)
функция достигает экстремума: в случае
имеется минимум, в случае
- максимум.
Если
,
то в данной критической точке экстремума
нет.
Пример. Исследовать на экстремум
функцию
.
Решение. Имеем элементарную функцию, определенную при любых действительных значениях переменных и . В соответствии с изложенным алгоритмом
а) Найдем частные производные
,
.
б) Найдем критические точки (точки, подозрительные на экстремум), из системы уравнений
,
которая в нашем случае имеет вид
или
Из первого уравнения системы
=
,
следовательно
Второе уравнение системы преобразуется к виду
,
откуда
,
.
Подставляя найденные значения поочерёдно
в первое уравнение системы, получим
,
.
Таким образом, заданная функция имеет
две критические точки
и
.
в) Найдем вторые частные производные данной функции:
Имеем в точке
:
Значит
=
в точке
,
а тогда в этой точке экстремума нет.
Далее, в точке
:
Следовательно,
=27>0,
так что в этой точке имеется экстремум.
Поскольку
,
то в точке
данная функция достигает минимума.
Определяем минимальное значение функции
:
Ответ:
.
2.5.2. Наибольшее и наименьшее значения функции в замкнутой ограниченной области D. Всякая непрерывная функция достигает в такой области D своего наибольшего и наименьшего значения. В частности, для элементарных функций может быть использован следующий алгоритм нахождения этих значений.
а) Найти частные производные и данной функции и определить критические точки, т.е. точки, в которых
;
при этом рассмотреть лишь те из них, которые расположены внутри области D.
б) Вычислить значения данной функции в этих точках.
в) Определить наибольшее и наименьшее значения функции на каждом участке границы области D. При этом, выражая переменную у или переменную х из уравнения соответствующего участка границы, будем всякий раз иметь функцию одной переменной на некотором отрезке. Исследование такой функции на наибольшее и наименьшее значение – знакомая задача (см. п. 1.5.1).
г) Среди значений, найденных в п. б) и в) выбрать наибольшее и наименьшее.
Пример. Найти наименьшее и
наибольшее значения функции
в замкнутой области D,
ограниченной линиями
,
,
.
Р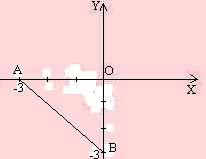
ешение.
Данная элементарная функция определена
при любых действительных значениях
переменных
и
.
Область
,
ограниченная указанными линиями,
изображена на рисунке
.
а) Найдем частные производные данной функции
,
и определим критические точки:
Преобразуем систему к виду
или
,
Откуда
и, следовательно,
.
Итак, данная функция имеет единственную
стационарную точку
,
которая, очевидно, принадлежит области
.
При этом
.
б) Исследуем поведение функции на границе области .
На участке границы
имеем функцию одной переменной
,
.
Тогда
и
,
если
,
откуда
.
Итак, нахождению подлежит значение
функции в точке
,
принадлежащей границе области
:
На участке границы
имеем функцию одной переменной
,
.
Тогда
и
при
.
В точке
,
принадлежащей границе области
,
имеем
Из уравнения прямой (участка границы)
выразим переменную
через
и подставим в заданную функцию. Получим,
что при
или
,
.
Далее,
и
,
если
,
откуда
.
Тогда
В точке
,
принадлежащей границе области
,
имеем
Остается вычислить значения данной функции в концевых точках участков границы (в угловых точках области ) и выбор наибольшего и наименьшего:
,
,
.
Сравнивая эти значения, находим, что
наибольшее из них равно 6 и достигается
в точках
,
,
а наименьшее значение равно -1 и достигается
в точке
.
Ответ:
достигается в точках
и
,
достигается в точке
.
Задачи для контрольной работы
Дана
функция
.
Найти
а) её точки экстремума;
б) наибольшее и наименьшее значения
данной функции в прямоугольнике,
ограниченном указанными прямыми
(значения
параметров
для каждого варианта указаны)
1.
. 14.
.
2.
. 15.
.
3.
. 16.
.
4.
. 17.
.
5.
. 18.
.
6.
. 19.
.
7.
. 20.
.
8.
. 21.
.
9.
. 22.
.
10.
. 23.
.
11.
. 24.
.
12.
. 25.
.
13.
.
СПИСОК ЛИТЕРАТУРЫ
Бермант, А.Ф. Краткий курс математического анализа : учебник. – 10-е изд., стереотип. / А.Ф.Бермант, И.Г. Араманович. – СПб. : Лань, 2003. – 736 с.
Пискунов, Н.С. Дифференциальное и интегральное исчисление. Т. 1: учебное пособие по математике для втузов.-13 издание. – М.: Наука, 1985. – 430 с.
Сборник индивидуальных заданий по высшей математике. Под ред. А.П. Рябушко Ч. 1-2. - Минск: Вышэйшая школа, 1991.-352 с.
Сборник задач по математике для втузов. В 4-х частях. Ч.1. Линейная алгебра и основы математического анализа. Под ред. А.В. Ефимова, Б.П. Демидовича. - М: Наука, 1993.-480 с.