
- •1.Дифференциальное исчисление функций одной переменной
- •1.1. Предел функции одной переменной
- •1.2. Производная функции одной переменной
- •1.3. Касательная и нормаль. Правило Лопиталя
- •1.4. Применение производной к исследованию функций
- •1.4.1. Исследование по первой производной: монотонность, экстремумы
- •1.4.2. Исследование по второй производной: характер выпуклости
- •1.4.3. Асимптоты графика
- •1.4.4. Алгоритм полного исследования функции
- •1.5. Нахождение наибольшего и наименьшего значения функции
- •1.5.2. Задачи о наибольших и наименьших значениях величин
- •2. Дифференциальное исчисление функций нескольких переменных
- •2.1. Частные производные.
- •Производная неявной функции.
- •Неявная функция одной переменной.
- •Неявная функция двух переменных.
- •2.3. Уравнение касательной плоскости и нормали.
- •2.4. Градиент и производная по направлению
- •2.5. Экстремумы функций двух переменных. Наибольшее и наименьшее значения.
- •2.5.1. Экстремумы функций двух переменных.
1.3. Касательная и нормаль. Правило Лопиталя
1.3.1. Касательная к графику
функции (кривой)
![]() ,
проведенная в точке
,
проведенная в точке
![]() ,
имеет уравнение
,
имеет уравнение
![]()
Нормаль, к графику функции (кривой)
![]() ,
проведенная в точке
,
проведенная в точке
![]() (т.е. перпендикуляр к касательной в точке
касания) в том случае, если
(т.е. перпендикуляр к касательной в точке
касания) в том случае, если
![]() имеет уравнение
имеет уравнение
![]()
Пример. Составить уравнения
касательной и нормали к кривой, заданной
уравнением
![]() ,
в точке
,
в точке
![]() .
.
Решение. В нашем случае точка касания
имеет (по условию задачи) координаты
![]() .
Вычислим
.
Вычислим
![]() тогда
тогда
![]() .
Уравнение
.
Уравнение
![]() или
или
![]() является уравнением касательной, а
уравнение
является уравнением касательной, а
уравнение
![]() или
или
![]() есть уравнение нормали к заданной кривой
в указанной точке.
есть уравнение нормали к заданной кривой
в указанной точке.
Задачи для контрольной работы
1.3.1.
Составить уравнение касательной
и нормали к кривой, заданной уравнением
,
в точке
![]() :
:
1.
![]() 14.
14.
![]()
2.
![]() 15.
15.
![]()
3.
![]() 16.
16.
![]()
4.
![]() 17.
17.
![]()
5.
![]() 18.
18.
![]()
6.
![]() 19.
19.
![]()
7.
![]() 20.
20.
![]()
8.
![]() 21.
21.
![]()
9.
![]() 22.
22.
![]()
10.
![]() 23.
23.
![]()
11.
![]() 24.
24.
![]()
12.
![]() 25.
25.
![]()
13.
![]()
1.3.2. Правило Лопиталя раскрытия
неопределенностей вида
и
![]() состоит в следующем: если существует
предел вида
состоит в следующем: если существует
предел вида
![]() ,
то
,
то
![]() =
.
=
.
Здесь а – некоторая точка или бесконечность любого знака.
Если отношение производных при
![]() снова есть неопределенность указанного
выше вида, то правило можно применить
снова, переходя ко вторым производным
и т.д.
снова есть неопределенность указанного
выше вида, то правило можно применить
снова, переходя ко вторым производным
и т.д.
Пример.
Вычислить
![]() .
.
Решение. Функции
![]() и
и
![]() бесконечно большие при
,
т.е. имеем неопределенность вида
бесконечно большие при
,
т.е. имеем неопределенность вида
![]() .
Применяем правило Лопиталя:
.
Применяем правило Лопиталя:
![]() =
=![]() .
Снова при
.
Снова при![]() имеем неопределенное выражение
.
Повторное применение правило Лопиталя
приводит к следующему результату:
имеем неопределенное выражение
.
Повторное применение правило Лопиталя
приводит к следующему результату:
![]()
Задачи для контрольной работы
1.3.2. Вычислить пределы:
1.
![]() 10.
10.
 18.
18.

2.
![]() 11.
11.
 19.
19.
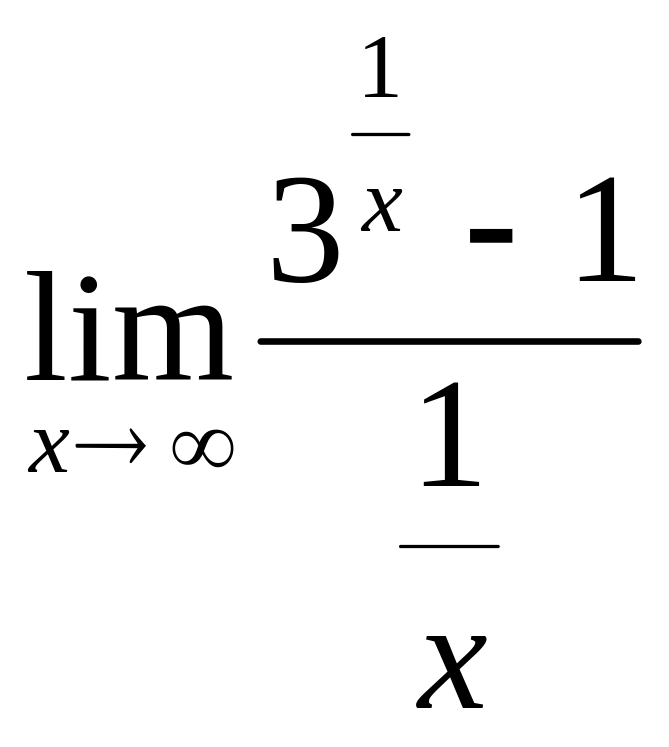
3.
![]() 12.
12.
![]() 20.
20.
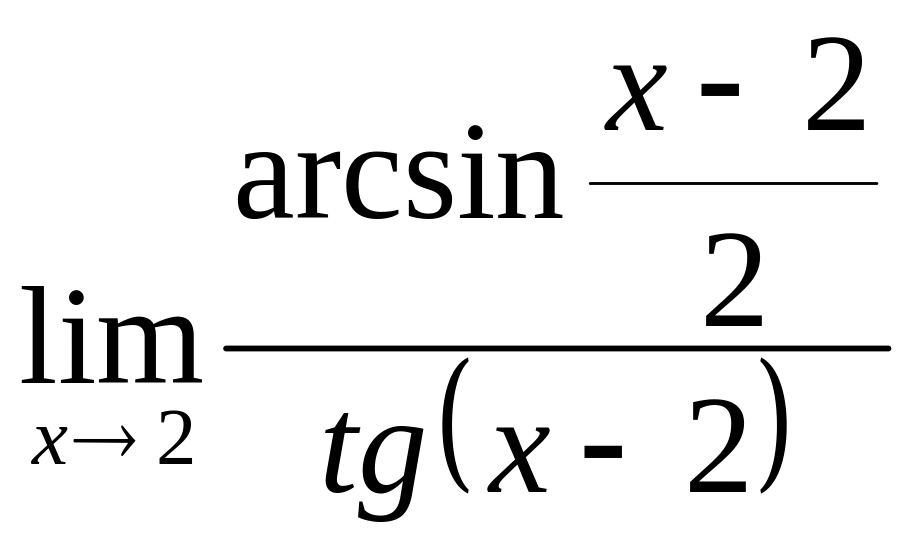
4.
![]() 13.
13.
![]() 21.
21.

5.
![]() . 14.
. 14.
![]() 22.
22.

6.
![]() 15.
15.
![]() 23.
23.
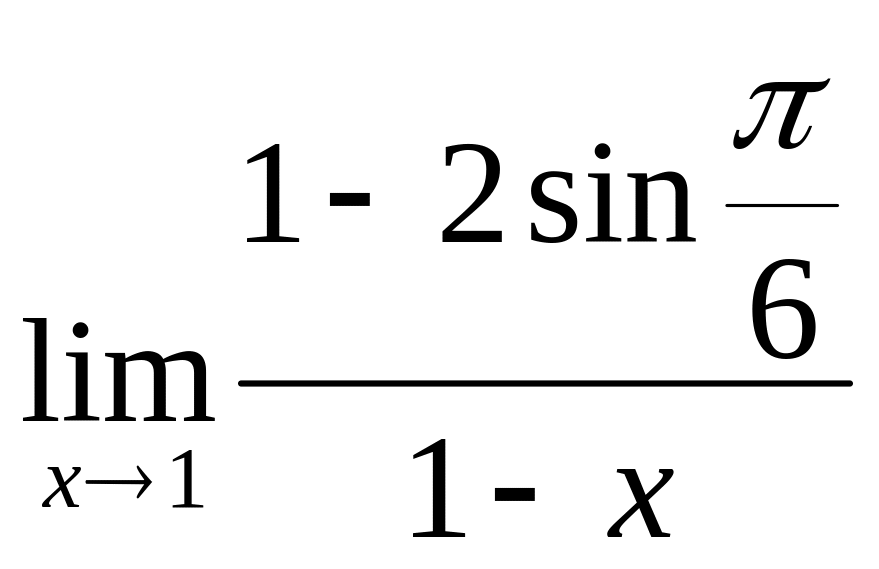
7.
![]() 16.
16.
![]() 24.
24.
![]()
8.
![]() 17.
17.
![]() 25.
25.
![]()
9.
![]()
1.4. Применение производной к исследованию функций
1.4.1. Исследование по первой производной: монотонность, экстремумы
В основе исследования функции на монотонность (возрастание, убывание) и экстремумы (максимумы, минимумы) лежат следующие положения:
а) интервалы, где, служат интервалами
возрастания функции
;
на интервалах, где
![]() ,
функция убывает;
,
функция убывает;
б) точки перемены знака с «+» на «-» служат точками максимума (точка наибольшего значения функции среди всех ее значений из некоторой окрестности этой точки) , а с «-» на «+» - точками минимума (точка наименьшего значения функции в некоторой окрестности).
1.4.2. Исследование по второй производной: характер выпуклости
Говорят, что дуга линии имеет определенный характер выпуклости, если она пересекается с любой своей секущей не более, чем в двух точках. Такая дуга лежит по одну сторону от касательной, проведенной в любой точке дуги: если целиком ниже касательной, то дуга называется выпуклой (выпуклой вверх), а если выше – то вогнутой (выпуклой вниз).
В основе исследования функции на характер выпуклости лежат следующие положения:
а) интервалы, где
![]() ,
служат интервалами вогнутости графика
функции
,
служат интервалами вогнутости графика
функции
![]() ;
на интервалах, где
;
на интервалах, где
![]() ,
график функции выпукл;
,
график функции выпукл;
б) точки перемены знака второй производной
![]() служат точками перегиба графика, т.е.
точками перемены характера выпуклости.
служат точками перегиба графика, т.е.
точками перемены характера выпуклости.
