1.2. Производная функции одной переменной
1.2.1. Если значение аргумента
функции
получило приращение
(изменилось на величину
),
то соответствующее приращение (изменение)
функции
есть
.
Величину
естественно назвать средней скоростью
изменения функции
,
соответствующей изменению аргумента
от х до х+
;
«мнговенной» же скоростью изменения
функции в точке х тогда следует
считать предел вида
называемый производной функции f
и обозначаемый
,
или
.
Операция взятия производной называется
дифференцированием функции.
Таблица производных основных элементарных функций.
1) 
; 9) 
;
2) 
; 10) 
;
3) 
; 11) 
;
4) 
; 12) 
;
5) 
; 13) 
;
6) 
; 14) 
;
7) 
; 15) 
;
8) 
; 16) 
.
Правила дифференцирования. Пусть
,
,
,
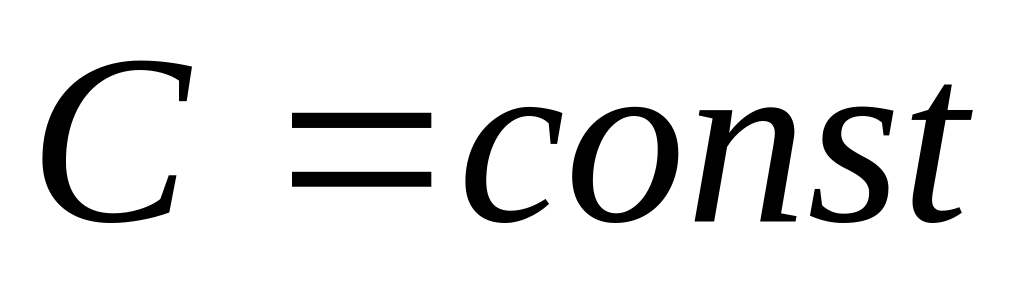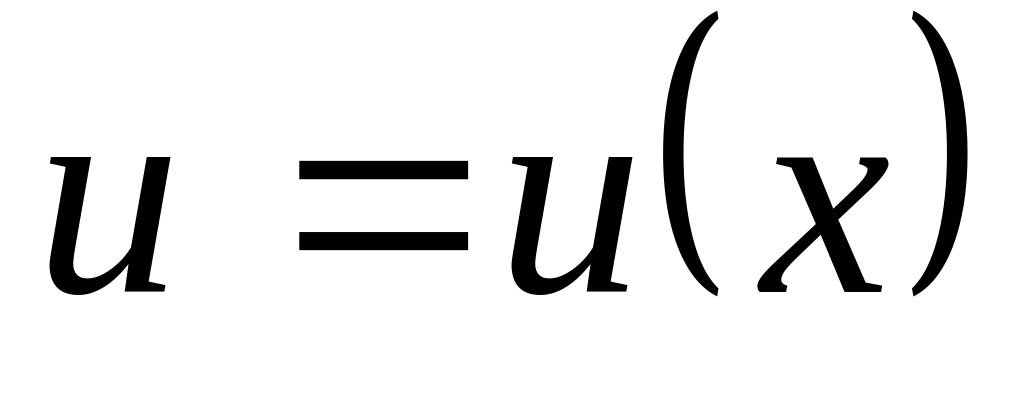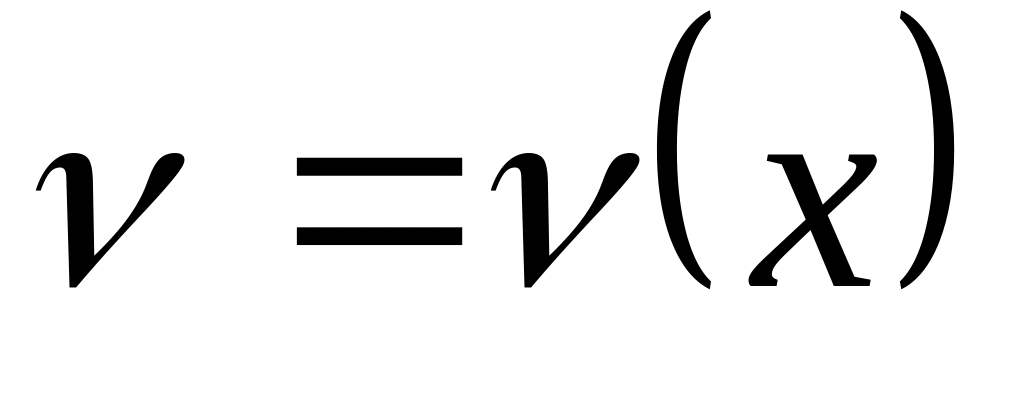тогда
1.
;
2.
;
3.
;
4.
.
Производная сложной функции
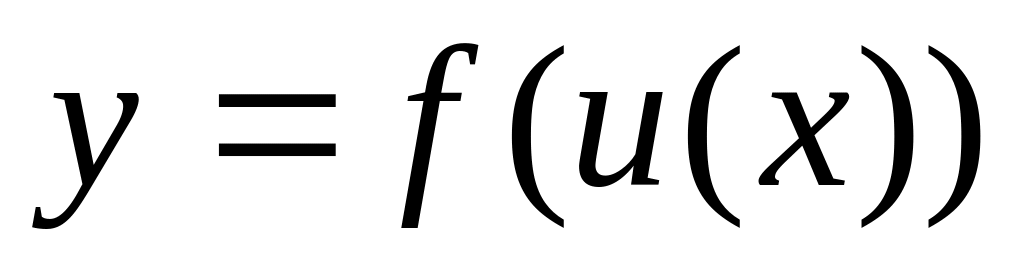вычисляется по правилу
,
где
Так, например,
Если зависимость
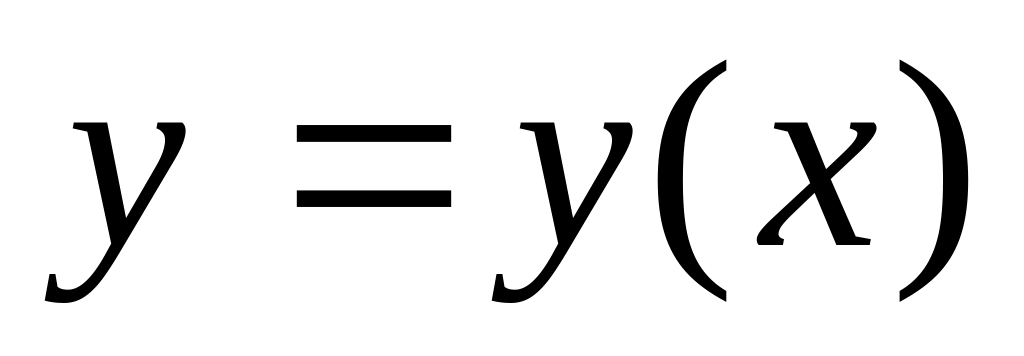задана параметрически, т.е. в виде
,
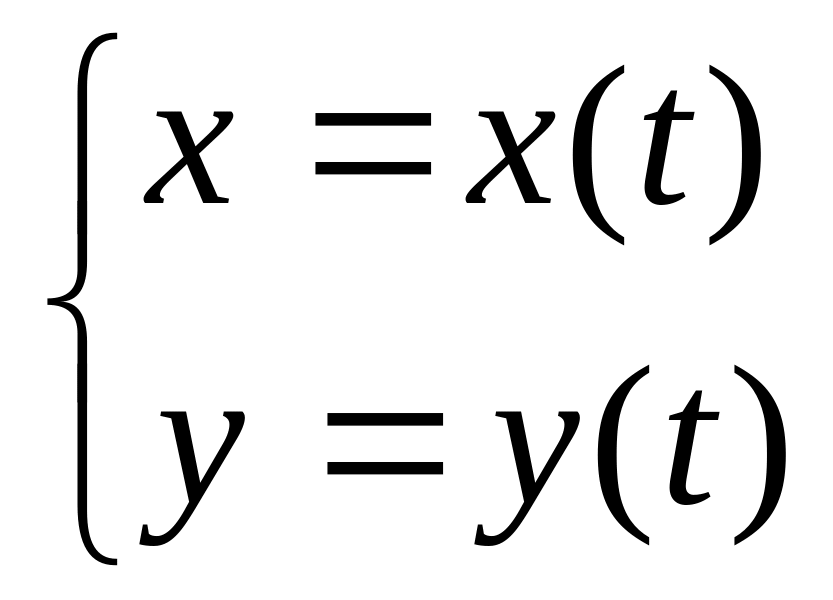то производная
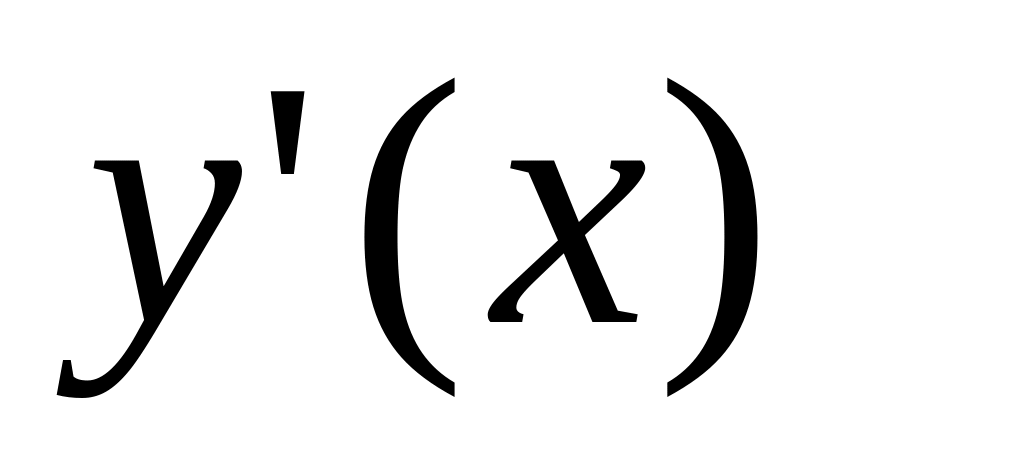(или,
в других обозначениях,
)
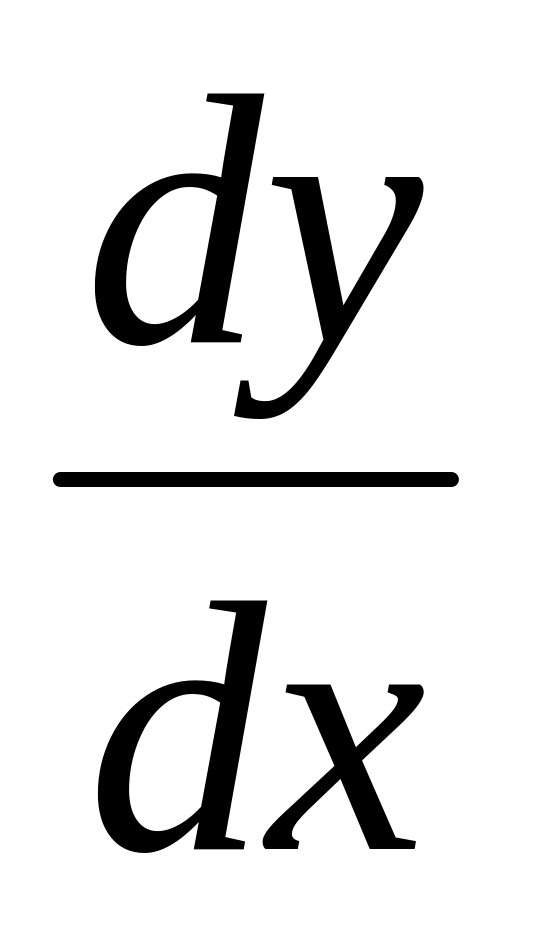вычисляется по формуле
1.2.6. Производная
также может рассматриваться как некоторая
функция; в этом случае можно говорить
о ее производной как второй производной
данной функции:
.
Аналогично можно рассматривать третью
и другие производные (производные высших
порядков).
Примеры.
1. Вычислить
,
если
.
Решение. В силу правил дифференцирования
.
Здесь мы имеем сложную логарифмическую
функцию, а именно функцию аргумента
.
По формуле дифференцирования натурального
логарифма «сложного аргумента» получаем
тогда
=
.
2. Материальная точка движется прямолинейно,
при этом зависимость пройденного
расстояния
от времени
(закон движения) имеет вид
.
Найти скорость
точки в момент
.
Решение. Согласно п.1.2.1 достаточно вычислить производную в точке . По формуле дифференцирования произведения и с учетом правила дифференцирования сложной функции мы имеем
3. Найти
производную функции, заданной
параметрически:
.
Решение.
Имеем:
,
а тогда по формуле дифференцирования
функции, заданной параметрически,
получаем
.
Задачи для контрольной работы
1.2
Найти производную функции
(в п.б функция у(х) задана
параметрически) :
1. а)
;
б)
2. а)
;
б)
3. а)
б)
4. а)
;
б)
5. а)
;
б)
6. а)
;
б)
7. а)
;
б)
8. а)
;
б)
9. а)
;
б)
10. а)
;
б)
11. а)
;
б)
12. а)
;
б)
13. а)
б)
14. а)
б)
15. а)
б)
16. а)
б)
17. а)
б)
18. а)
б)
19. а)
б)
20. а)
б)
21. а)
б)
22. а)
б)
23. а)
б)
24. а)
б)
25. а)
б)
