- •1.Дифференциальное исчисление функций одной переменной
- •1.1. Предел функции одной переменной
- •1.2. Производная функции одной переменной
- •1.3. Касательная и нормаль. Правило Лопиталя
- •1.4. Применение производной к исследованию функций
- •1.4.1. Исследование по первой производной: монотонность, экстремумы
- •1.4.2. Исследование по второй производной: характер выпуклости
- •1.4.3. Асимптоты графика
- •1.4.4. Алгоритм полного исследования функции
- •1.5. Нахождение наибольшего и наименьшего значения функции
- •1.5.2. Задачи о наибольших и наименьших значениях величин
- •2. Дифференциальное исчисление функций нескольких переменных
- •2.1. Частные производные.
- •Производная неявной функции.
- •Неявная функция одной переменной.
- •Неявная функция двух переменных.
- •2.3. Уравнение касательной плоскости и нормали.
- •2.4. Градиент и производная по направлению
- •2.5. Экстремумы функций двух переменных. Наибольшее и наименьшее значения.
- •2.5.1. Экстремумы функций двух переменных.
УДК
ББК
Рекомендовано редакционно-издательским советом университета
Рецензент
Кандидат технических наук доцент ГОУ ВПО ТГТУ
Е.Е. Мордовина
|
Нахман А. Д., Петрова Е.А. |
|
«Дифференциальное исчисление функций одной и нескольких переменных»: Методические указания и контрольные задания. Тамбов: Изд-во ГОУВПО ТГТУ, 2012. - 32 с. ISBN |
|
Приведены краткие теоретические сведения и алгоритмы решения стандартных задач по разделу курса математики "Дифференциальное исчисление функций одной и нескольких переменных". Предложены 25 вариантов контрольных заданий. Для студентов очной и заочной форм обучения. |
Введение
Настоящие методические разработки подготовлены в соответствии с требованиями ФГОС ВПО к основным образовательным программам естественно-математической подготовки бакалавров. Издание адресовано студентам 1 курса инженерных направлений. Целью издания является формирование и закрепление навыков в области решения задач по дифференциальному исчислению функций одной и нескольких переменных. В силу ограниченного объема работы авторы избегали точных формулировок основных определений и теорем, ограничиваясь объяснением смысла понятий и утверждений. По этой причине, студенту предварительно следует ознакомиться с соответствующим теоретическим материалом по учебнику или конспекту лекций.
Работа построена по модульному принципу. Речь идет о следующих модулях содержания:
предел и производная функции одной переменной, приложения производной (в том числе, к исследованию функций), частные производные функций нескольких переменных, приложения дифференциального исчисления функций нескольких переменных (в том числе, в теории скалярного поля и к исследованию экстремального поведения функций).
Образцы решений типовых задач предваряются изложением соответствующего алгоритма. Каждый параграф заканчивается перечнем контрольных заданий. Задачи составлены так, чтобы в процессе их решения не возникали технические трудности, преодоление которых «затушевывает» суть дела. Преподаватель, по своему усмотрению, может варьировать объем и уровень трудности заданий. Так, например, в заданиях на исследование функции минимальные требования могут быть сведены лишь к применению первой производной (исследование характера монотонности и экстремумов функции). Банк предлагаемых здесь задач может быть использован для формирования контрольных работ, адресованных студентам как очной, так и заочной форм обучения.
1.Дифференциальное исчисление функций одной переменной
1.1. Предел функции одной переменной
1.1.1. Понятие предела – одно
из основных в математическом анализе.
Не приводя строгих определений, объясним
смысл указанного понятия. Пусть дана
функция
![]() и значения аргумента х неограниченно
приближаются к значению
и значения аргумента х неограниченно
приближаются к значению
![]() ,
но не совпадают с
(что будем записывать в виде
,
но не совпадают с
(что будем записывать в виде
![]() ).
Если при этом оказывается, что значения
становятся сколь угодно близкими к
некоторому числу А, то говорят, А
есть предел функции
).
Если при этом оказывается, что значения
становятся сколь угодно близкими к
некоторому числу А, то говорят, А
есть предел функции
![]() в точке
и записывают
в точке
и записывают
![]()
![]() .
.
В случае, когда значения аргумента х
неограниченно растут по модулю, оставаясь
при этом положительными (отрицательными),
мы записываем
![]() (
(![]() ).
Если не принципиально, какого знака
значения аргумента х, то употребляем
символ
).
Если не принципиально, какого знака
значения аргумента х, то употребляем
символ
![]() Запись
Запись
![]() означает,
что значения
становятся сколь угодно близкими к
числу А при
Говорят также, что число А есть
предел функции на бесконечности.
означает,
что значения
становятся сколь угодно близкими к
числу А при
Говорят также, что число А есть
предел функции на бесконечности.
Если в (любом из трех рассмотренных
случаев) А=0, то функция
![]() называется
бесконечно малой.
называется
бесконечно малой.
Возможен также случай, когда значения
функции
неограниченно
растут (к
![]() или -
или -![]() )
при стремлении аргумента х к
некоторому
или
к бесконечности. В этих случаях записывают
соответственно
)
при стремлении аргумента х к
некоторому
или
к бесконечности. В этих случаях записывают
соответственно
![]() и
и
![]() ,
,
а функцию
называют
бесконечно большой (при
и
![]() соответственно).
соответственно).
Следует заметить, что если функция
- бесконечно большая (бесконечно малая),
то функция
![]() бесконечно малая (бесконечно большая).
бесконечно малая (бесконечно большая).
Если рассмотреть, в частности, функцию
натурального аргумента (последовательность)
![]() ,
то к ней применимо определение предела
на бесконечности; используют запись
,
то к ней применимо определение предела
на бесконечности; используют запись
![]() .
.
1.1.2. Всякая элементарная
функция
![]() непрерывна на своей области определения
непрерывна на своей области определения
![]() .
Это означает возможность перехода к
пределу под знаком функции
во всякой точке
.
Это означает возможность перехода к
пределу под знаком функции
во всякой точке
![]() :
:
![]() .
.
Этим свойством пользуются при вычислении пределов. Кроме того, при выполнении арифметических операций над функциями соответствующие операции выполняются и над их пределами.
1.1.3. Неопределенностями (при
или
)
называются такие выражения (под знаком
предела), которые при формальной
подстановке вместо аргумента х
предельного значения (![]() или
или
![]() )
принимают вид
)
принимают вид
![]() ,
,
![]() и др.
и др.
1.1.4. Приемы вычисления пределов. Вычисление пределов рациональных или иррациональных дробей на бесконечности может быть произведено путем одновременного деления числителя и знаменателя на старшую степень аргумента, чем достигается переход от бесконечно больших к бесконечно малым. Продемонстрируем прием на следующем примере.
Пример. Вычислить
![]() .
.
Решение. Имеем бесконечно большие
в числителе и знаменателе дроби;
следовательно, выполняем одновременное
деление на старшую степень аргумента,
т.е. на
![]()
![]() =
=
Теперь имеем бесконечно малую в
знаменателе дробь и функцию, стремящуюся
к
![]() в числителе, т.е. дробь оказывается
бесконечно большой. Ответ записываем
в виде
в числителе, т.е. дробь оказывается
бесконечно большой. Ответ записываем
в виде
![]() .
.
Пример.
Вычислить
![]() .
.
Решение.
Имеем неопределенность
вида
![]() .
Для ее раскрытия умножим числитель и
знаменатель на выражение сопряженное
числителю, т.е. на
.
Для ее раскрытия умножим числитель и
знаменатель на выражение сопряженное
числителю, т.е. на
![]() и сократим числитель и знаменатель на
общий множитель х
, (который при
и сократим числитель и знаменатель на
общий множитель х
, (который при
![]() не
равен нулю). В результате имеем
не
равен нулю). В результате имеем
![]()
так что искомый предел равен 0,5.
1.1.5. Замечательные пределы.
1) При
![]() отношение
отношение
![]() представляет собою неопределенность
вида
представляет собою неопределенность
вида
![]() .
Можно доказать, что
.
Можно доказать, что
![]() .
.
2) При
показательно-степенное выражение вида
![]() представляет собою неопределенность
вида
представляет собою неопределенность
вида
![]() .
Можно доказать, что соответствующий
предел существует и равен некоторому
иррациональному числу е=2,7…:
.
Можно доказать, что соответствующий
предел существует и равен некоторому
иррациональному числу е=2,7…:
![]() .
.
Рассмотренные пределы называются , соответственно, первым и вторым замечательными пределами. Второй замечательный предел может быть также записан в равносильной форме
![]() .
.
Пример.
Вычислить a)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
Решение. а) Имеем неопределенность
вида
![]() .
Заметим, что при
.
Заметим, что при
![]() (см.
первый замечательный предел) отношение
(см.
первый замечательный предел) отношение
![]() (вместе
с
(вместе
с
![]() )
стремится к единице. При вычислении
предела отношения
)
стремится к единице. При вычислении
предела отношения
![]() можно снова воспользоваться первым
замечательным пределом, если положить
можно снова воспользоваться первым
замечательным пределом, если положить
![]() и
заметить, что
и
заметить, что
![]() при
при
![]() .
Остается выполнить преобразование
.
Остается выполнить преобразование
![]() =
=![]()
и закончить вычисление:
=3![]()
![]()
б) Имеем «комбинированную» неопределенность
вида
![]() .
Если выделить в скобках в качестве
слагаемого число 1, то станет возможным
использование второго замечательного
предела:
.
Если выделить в скобках в качестве
слагаемого число 1, то станет возможным
использование второго замечательного
предела:
=![]() .
.
Теперь
![]() при
при
![]() ,
поэтому в показателе степени удобно
выделить выражение вида
,
поэтому в показателе степени удобно
выделить выражение вида
![]() ,
т.е.
,
т.е.
![]() :
:
=![]() .
.
Теперь, пользуясь свойством непрерывности показательно-степенной функции, перейдем по-отдельности к пределу в основании и показателе степени:
![]() (второй замечательный предел при
(второй замечательный предел при
![]() ),
),

Имеем
![]() .
.
в) Непосредственная подстановка значения
![]() приводит к неопределенному выражению
вида
приводит к неопределенному выражению
вида
![]() .
Снова используем прием выделения
слагаемого, равного 1:
.
Снова используем прием выделения
слагаемого, равного 1:
![]() =
=![]()
Задачи для контрольной работы
Вычислить пределы:
1. а)
![]() б)
б)
![]() в)
в)

2. а)![]() б)
б)
![]() в)
в)
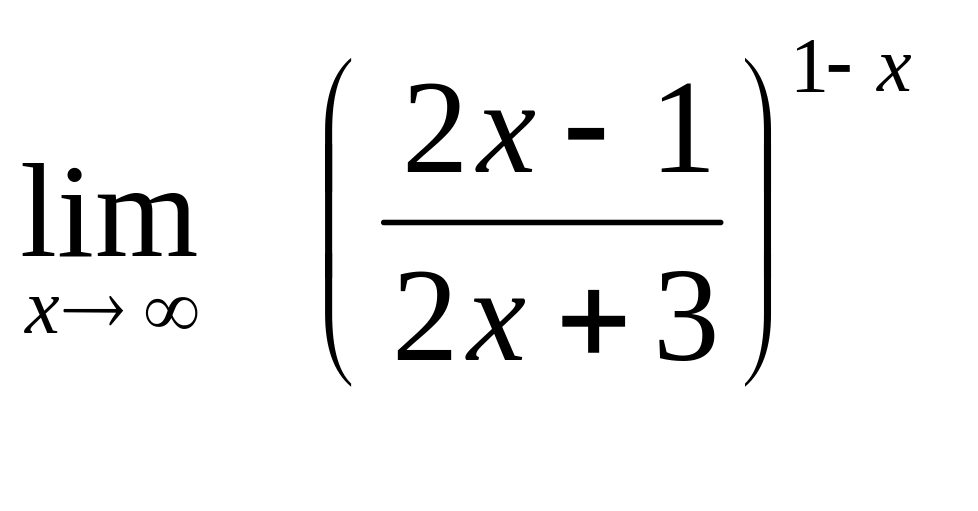
3. а)
![]() б)
б)
![]() в)
в)

4. а)
![]() б)
б)
![]() в)
в)

5. а)
![]() б)
б)
![]() в)
в)
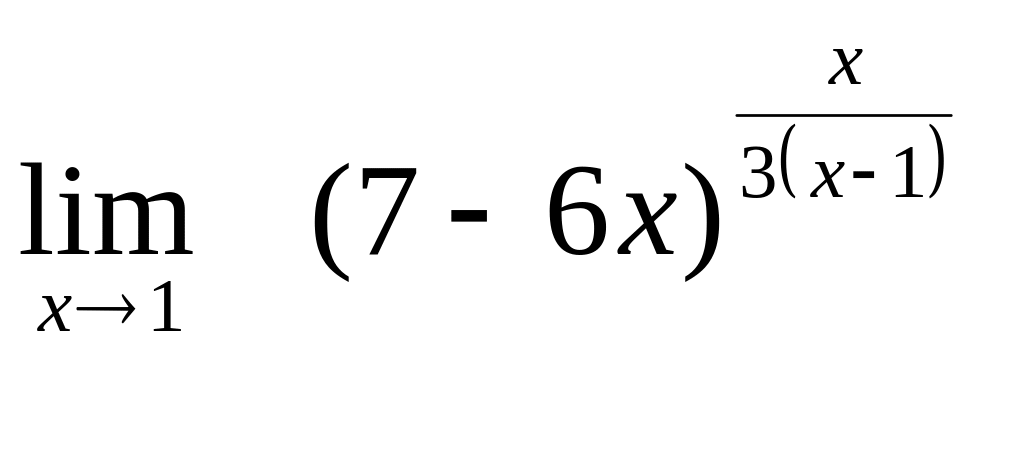
6. а)
![]() б)
б)
![]() в)
в)
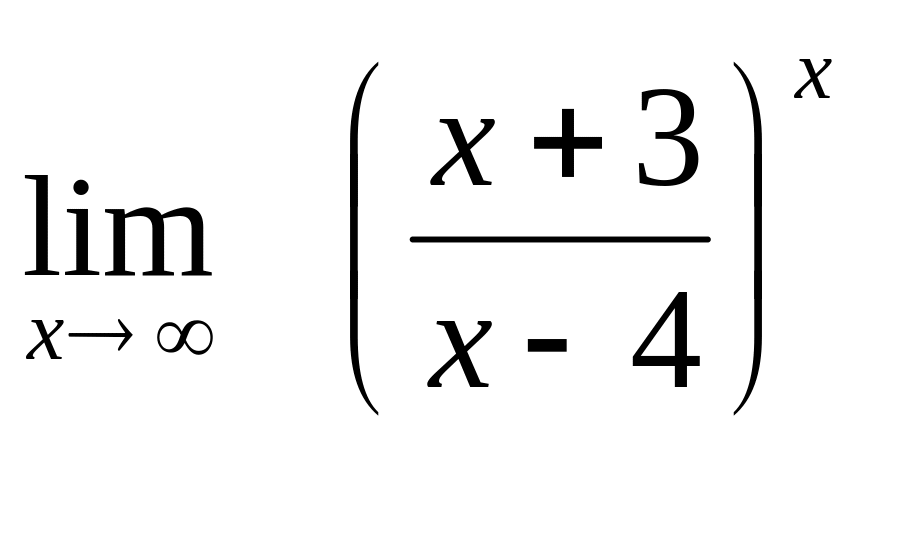
7. а)
![]() б)
б)
![]() в)
в)
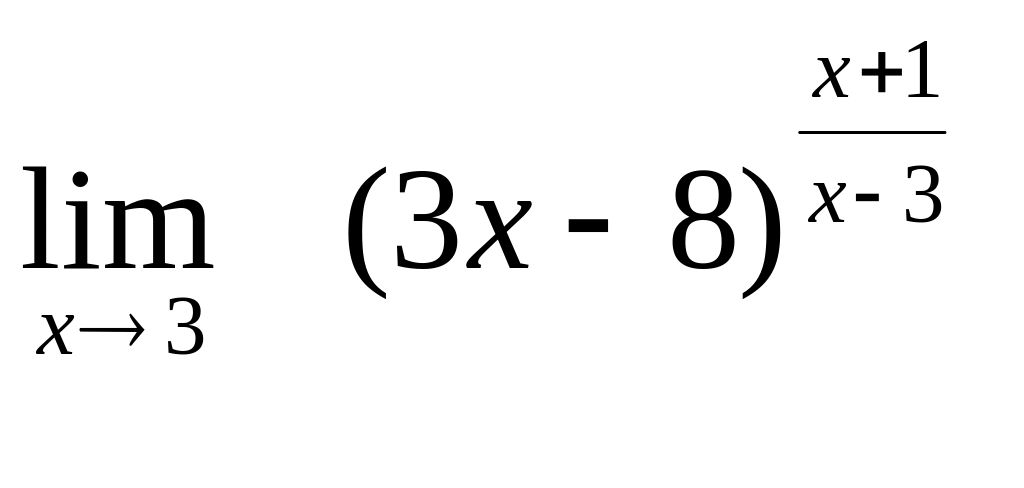
8. а)
![]() б)
б)
![]() в)
в)

9. а)
![]() б)
б)
![]() в)
в)
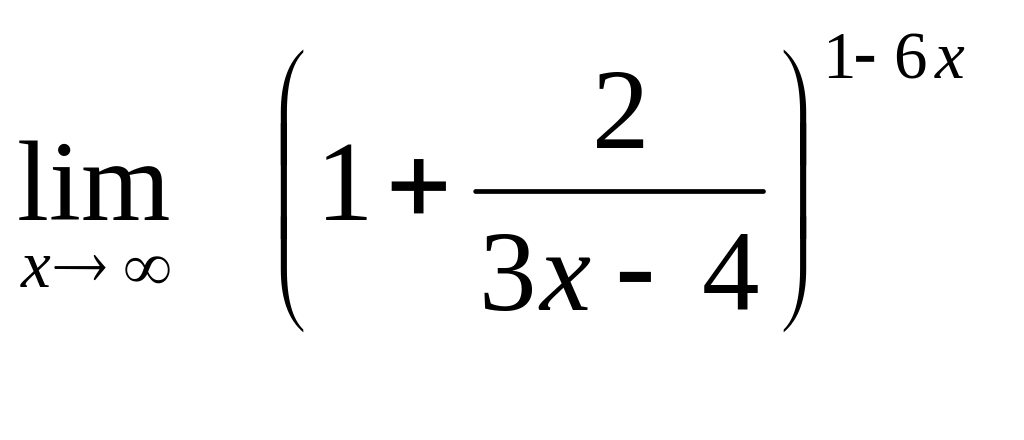
10. а)
![]() б)
б)
![]() в)
в)

11. а)
![]() б)
б)
![]() в)
в)
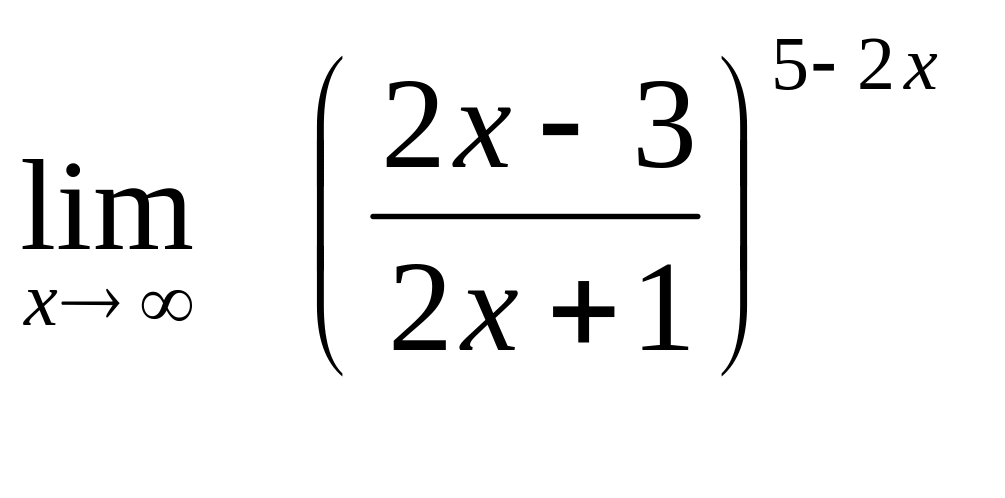
12. а)
![]() б)
б)
![]() в)
в)
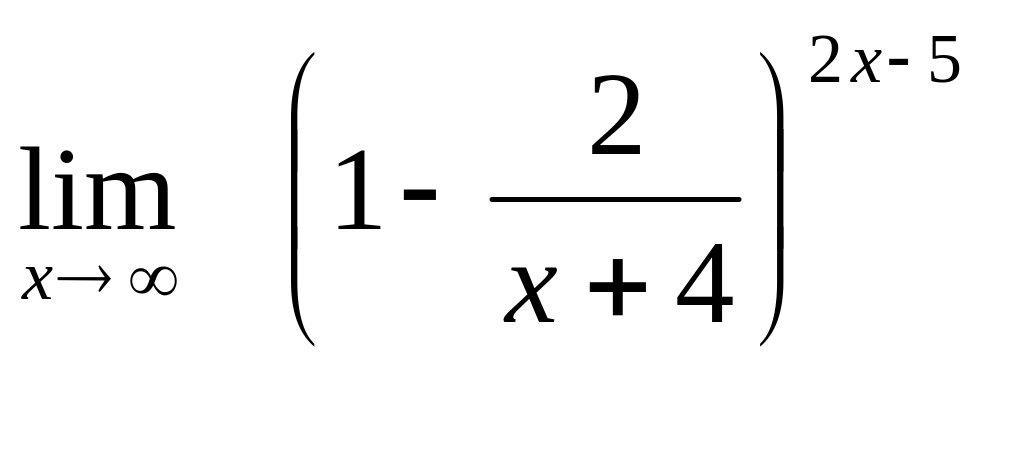
13. а)
![]() б)
б)
![]() в)
в)

14. а)
![]() б)
б)
![]() в)
в)

15. а)
![]() б)
б)
![]() в)
в)

16. а)
![]() б)
б)
![]() в)
в)
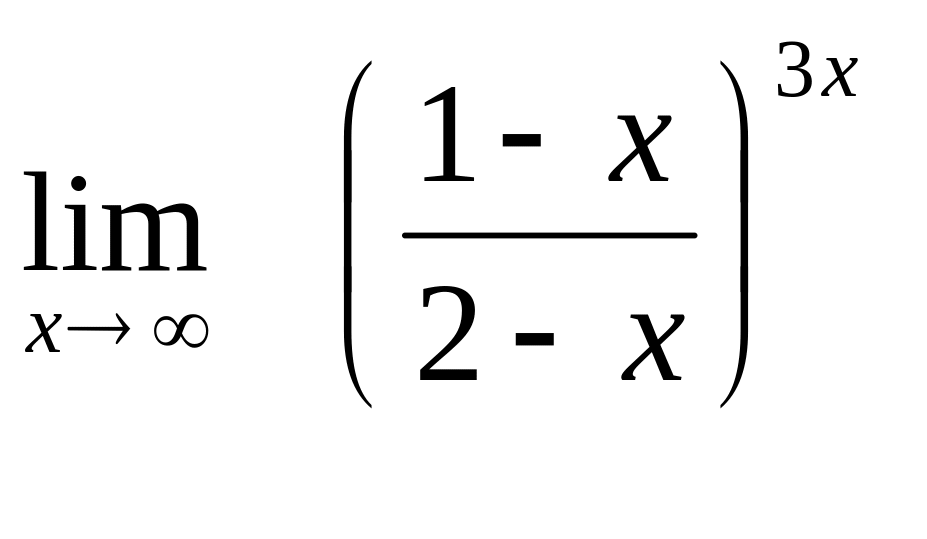
17. а)
![]() б)
б)
![]() в)
в)
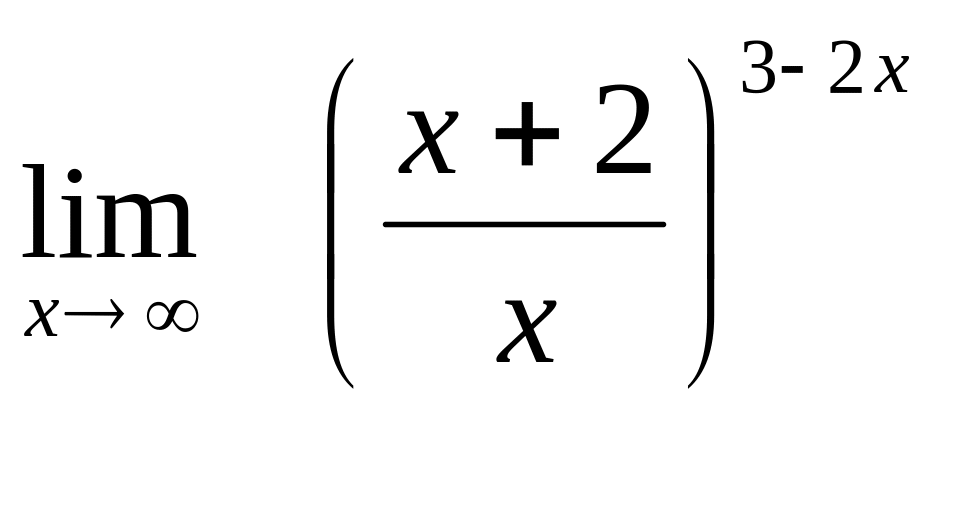
18. а)
![]() б)
б)
![]() в)
в)

19. а)
![]() б)
б)
![]() в)
в)
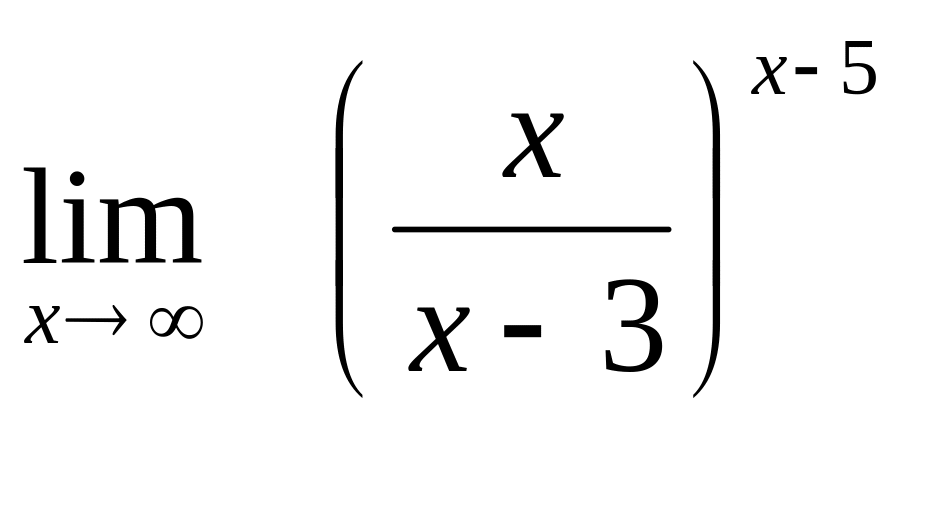
20. а)
![]() б)
б)
![]() в)
в)
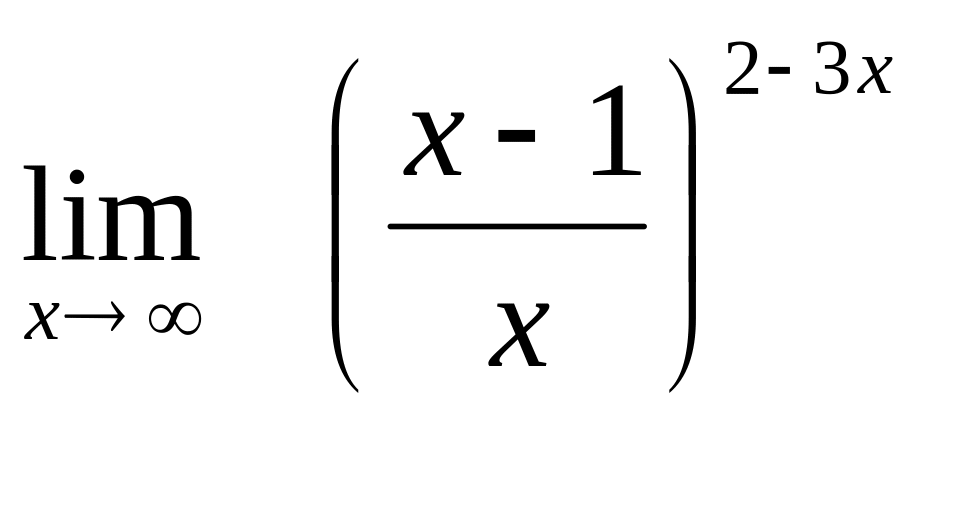
21. а)
![]() б)
б)
![]() в)
в)
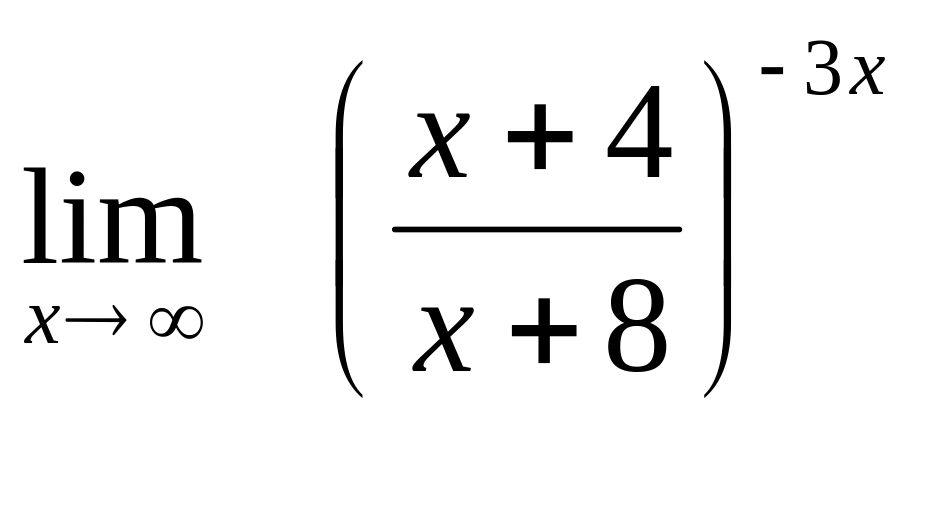
22. а)
![]() б)
б)
![]() в)
в)

23. а)
![]() б)
б)
![]() в)
в)
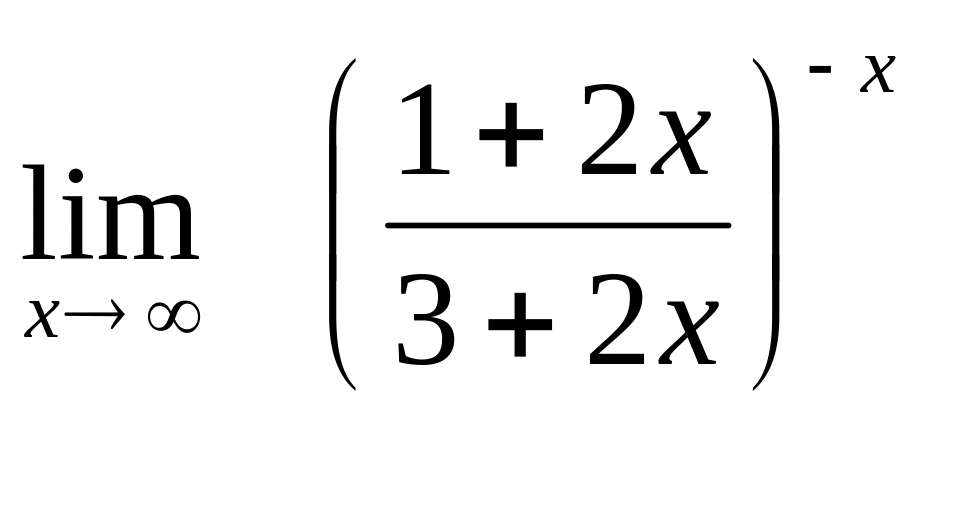
24. а)
![]() б)
б)
![]() в)
в)

25. а)
![]() б)
б)
![]() в)
в)