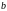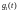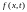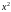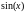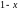Приложение 2.B
Д
ля
нахождения решения стационарного
уравнения теплопроводности
дважды проинтегрируем его. Первое
интегрирование дает такой результат
.
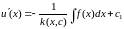Проинтегрируем полученное соотношение еще раз получим:
.
Константы
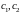находятся из граничных условий:
,
.
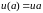Пример
решения задачи 2.1. Пусть
.
,
,
.
Проинтегрируем
уравнение:
.
Повторное интегрирование дает
соотношение:
.
Найдем
константы
и
,
при условии, что
:
;
,
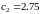
поэтому
.
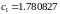Окончательно,
решение примет вид:
.
Для проверки можно подставить найденное решение в исходное уравнение и проверить выполнение граничных условий.
Вместо задачи 2.6
Найти приближенное решение начально-краевой задачи для уравнения теплопроводности:
используя
явную разностную схему. Взять
;
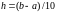шаг
выбрать из условия устойчивости.
Изобразить графики зависимости
приближенного решения от
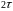при t=
,
,
,…T.
УКАЗАНИЕ.
Условие устойчивости для явной разностной
схемы имеет вид
.
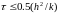Таблица к задаче 22
№ |
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
0.05 |
0 |
0 |
0 |
x |
2 |
-1 |
1 |
0.5 |
0.4 |
|
1 |
1 |
0 |
3 |
0 |
1 |
0.1 |
0.5 |
x (1-x) |
5t |
5t |
0 |
4 |
0 |
2 |
1 |
0.2 |
0 |
0 |
0 |
x |
5 |
0 |
1 |
0.1 |
0.5 |
x |
|
|
0 |
6 |
-1 |
1 |
2 |
0.1 |
|
1 |
1 |
0 |
7 |
0 |
1 |
2 |
0.02 |
0 |
0 |
|
x (1-x) |
8 |
-1 |
1 |
0.5 |
0.4 |
|
0 |
0 |
x |
9 |
0 |
1 |
0.1 |
0.5 |
|
0 |
1 |
t |
10 |
-1 |
1 |
0.2 |
1 |
0 |
0 |
0 |
|
11 |
0 |
1 |
1 |
0.05 |
|
0.5 |
0.5 |
0 |
12 |
-1 |
1 |
0.5 |
0.4 |
|
1 |
1 |
x |
13 |
0 |
1 |
0.2 |
0.25 |
|
0 |
|
|
14 |
0 |
2 |
1 |
0.2 |
|
0 |
|
|
15 |
0 |
1 |
1 |
0.05 |
1 |
|
|
0 |
16 |
0 |
2 |
1 |
0.2 |
1 |
|
|
0 |
17 |
0 |
1 |
0.5 |
0.1 |
1 |
|
|
2 |
18 |
0 |
2 |
0.5 |
0.4 |
1 |
|
|
2 |
19 |
0 |
1 |
0.2 |
0.2 |
|
1 |
0 |
0 |
20 |
0 |
2 |
2 |
0.1 |
0 |
0 |
10t |
1 |
21 |
0 |
1 |
0.5 |
0.1 |
0 |
0 |
10t |
t |
22 |
0 |
2 |
1 |
0.2 |
1 |
|
|
1 |
23 |
0 |
1 |
0.4 |
0.1 |
x |
0 |
1 |
1 |
24 |
-1 |
1 |
1 |
0.2 |
|
0 |
5t |
0 |
25 |
0 |
1 |
0.4 |
0.1 |
|
1 |
0 |
2 |
26 |
0 |
2 |
1 |
0.2 |
x |
0 |
2 |
x |
27 |
0 |
1 |
0.25 |
0.2 |
|
0 |
1 |
5 |
28 |
0 |
2 |
1 |
0.2 |
x |
0 |
2 |
x |
29 |
0 |
1 |
0.5 |
0.1 |
0 |
0 |
-1 |
1 |
30 |
-1 |
1 |
0.2 |
1 |
1- |
0 |
0 |
1 |
