
- •Математика
- •Общие указания по подготовке к фэпо
- •Основная литература
- •Дополнительная литература
- •Электронные ресурсы
- •Раздел 1. Алгебра и геометрия
- •1. Определители
- •2. Матрицы
- •3. Векторная алгебра
- •Раздел 2. Математический анализ
- •Раздел 3. Дифференциальные уравнения
- •Раздел 4. Теория функций комплексного переменного.
- •Раздел 5. Теория вероятностей.
- •Раздел 6. Численные методы
- •2.Графический способ
- •1 Численные методы решения алгебраических уравнений
- •Раздел 7. Дискретная математика и абстрактная алгебра
- •664074, Иркутск, Лермонтова, 83
Раздел 6. Численные методы
Приближённые решения конечных уравнений.
Численные решения уравнений f(x) = 0 складываются из 2-х этапов.
1. Отделение корней, то есть установление промежутков, внутри которых находится один и только один корень (интервал изоляции корня).
2. Вычисление корней с заданной степенью точности.
Отделение корней
1. Аналитический способоснован на свойствах непрерывных функций на
отрезке и монотонности функций.
Если
f(x)
непрерывна на [ и
и
 то f(x)
пересекает ось ох в точке с
то f(x)
пересекает ось ох в точке с
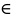 [
;
[
;
f(x)

 [
[
0
 bx
bx
2.Графический способ
П усть
требуется определить интервал изоляции
корня для уравнения f(x)
= f1(x)
+ f2(x)
= 0 . Корень этого уравнения это точка
пересечения графиков y
= f1(x)
и y=
f2
(x)
. yy2
усть
требуется определить интервал изоляции
корня для уравнения f(x)
= f1(x)
+ f2(x)
= 0 . Корень этого уравнения это точка
пересечения графиков y
= f1(x)
и y=
f2
(x)
. yy2

y1
0 x0x
Для
приближенного нахождения х*
отрезок [
делят пополам и вычисляют значение
f(x1)
в средней точке x1=(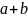 )/2.
Если отрезка два, то из двух отрезков
[
,
х1]и
[ х1,
b] для последующего деления пополам
выбирается тот, на концах которого
значения функции различны по знаку.
Возникающая в процессе такого дробления
последовательность середин отрезков
х1,
х2,
. . . сходится к корню х * со скоростью
геометрической прогрессии
)/2.
Если отрезка два, то из двух отрезков
[
,
х1]и
[ х1,
b] для последующего деления пополам
выбирается тот, на концах которого
значения функции различны по знаку.
Возникающая в процессе такого дробления
последовательность середин отрезков
х1,
х2,
. . . сходится к корню х * со скоростью
геометрической прогрессии
Интерполяционная
формула Лагранжа


Интерполяционный многочлен Лагранжа второй степени для таблицы вида
|
|
|
|
|
|
|
|
имеет
вид

Приближённое значение функции имеет вид
.
Приближенное значение функции двух переменных имеет вид
Численное интегрирование
Приближённое вычисление определённых интегралов
Пусть
на
 задана непрерывная функция y
задана непрерывная функция y .
.

 ,
,
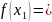 , … ,
, … ,


Тогда
 -
формула «левых» прямоугольников
-
формула «левых» прямоугольников
 -
формула «правых» прямоугольников
-
формула «правых» прямоугольников
 – формула
трапеций
– формула
трапеций
 ,
где n=2m
,
,
где n=2m
,
 – формула парабол или Симпсона
– формула парабол или Симпсона
Ряды Тейлора и Маклорена
Ряд Тейлора:
Ряд Маклорена:
.
Разложение элементарных функций в ряд Маклорена
Контрольные задания к разделу №6
1 Численные методы решения алгебраических уравнений
1.1 |
Положительный
корень уравнения
|
А)
В) С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение:
|
||||||||||||||||||||||||||||||||||||||
1.2 |
Три
итерации метода половинного деления
при решении уравнения
|
А) х1=4 х2=2 х3=3 B) х1=4 х2=6 х3=5 C) х1=4 х2=3 х3=2 D) х1=1 х2=2 х3=3 |
|||||||||||||||||||||||||||||||||||||
|
Решение: Выберем отрезок
Х1=(0+8)/2=4 Выберем
отрезок
Выбранный
отрезок не подходит так как
Выберем
отрезок
Х2=(0+4)/2=2 Выберем
отрезок
Х3=(2+4)/2=3 х1=4 х2=2 х3=3 |
||||||||||||||||||||||||||||||||||||||
1.3 |
Действительный
корень уравнения
|
А)
В) С)
D) |
|||||||||||||||||||||||||||||||||||||
|
Решение
х=0
|
||||||||||||||||||||||||||||||||||||||
1.4 |
Положительный
корень уравнения
|
А) В) С) D) |
|||||||||||||||||||||||||||||||||||||
|
Решение y1=lnxy2=1/x
|
||||||||||||||||||||||||||||||||||||||
1.5 |
Три
итерации метода половинного деления
при решении уравнения
|
А) х1=4 х2=2 х3=3 В) х1=4 х2=2 х3=1 С) х1=4 х2=1 х3=2 D) х1=3 х2=2 х3=1 |
|||||||||||||||||||||||||||||||||||||
|
Решение: Выберем отрезок
Х1=(0+8)/2=4 Выберем отрезок
Х2=(0+4)/2=2 Выберем отрезок
Выберем
отрезок
Х2=(0+2)/2=1 В) х1=4 х2=2 х3=1 |
||||||||||||||||||||||||||||||||||||||
2 |
Численное дифференцирование и интегрирование |
||||||||||||||||||||||||||||||||||||||
2.1 |
Значение функции в точке можно вычислить по формуле: |
А) ; В) ; С) ; D) . |
|||||||||||||||||||||||||||||||||||||
|
Решение ; ; . |
||||||||||||||||||||||||||||||||||||||
2.2 |
Значение
функции
|
А) В)
С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение
;
; |
||||||||||||||||||||||||||||||||||||||
2.3 |
Значение дифференцируемой функции в точке х=2,28 можно приближённо найти как |
А)
В) С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение
|
||||||||||||||||||||||||||||||||||||||
2.4 |
Значение
с точностью до 0,01 равно |
А) 4,08 В) С) 4,13 D) 4,09 |
|||||||||||||||||||||||||||||||||||||
|
Решение:
x0
+
|
||||||||||||||||||||||||||||||||||||||
2.5 |
Значение
|
А) 0,8 В) С) 0,9 D) 0,73 |
|||||||||||||||||||||||||||||||||||||
|
Решение
x0
+
=1,03 x0
=1
|
||||||||||||||||||||||||||||||||||||||
2.6 |
Значение
дифференциала функции
в точке (1,08;-1,01) равно |
А) -0,035 В) С) -0,045 D)
– |
|||||||||||||||||||||||||||||||||||||
|
Решение
x0
+
=1,08 x0
=1
у0
+
Тогда
|
||||||||||||||||||||||||||||||||||||||
2.7 |
Значение
дифференцируемой функции
в точке (2,01; 2,08) можно приближённо найти как |
А)
В) С) D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение
x0
+
=2,01 x0
=2
у0
+
=2,08 у0
=2
|
||||||||||||||||||||||||||||||||||||||
2.8 |
Значение дифференцируемой функции в точке х=0,97можно приближённо найти как |
А)
В) С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение
|
||||||||||||||||||||||||||||||||||||||
2.9 |
Значение
интеграла
|
А) 0,8 В) 0,9 С) 1 D) 0,6 |
|||||||||||||||||||||||||||||||||||||
|
Решение
|
||||||||||||||||||||||||||||||||||||||
2,10 |
Значение
интеграла
|
А) 0,9 В) 0,98 С) 1 D) 0,94 |
|||||||||||||||||||||||||||||||||||||
|
Решение
|
||||||||||||||||||||||||||||||||||||||
2.11 |
Значение
определённого интеграла
|
А)
В) С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение
Разделим
отрезок [ Пусть
|
||||||||||||||||||||||||||||||||||||||
2.12 |
Значение определённого интеграла по формуле трапеций можно найти: |
А)
В) С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение
Разделим отрезок [ точками на n равных частей длины Пусть
Y6=0,8
|
||||||||||||||||||||||||||||||||||||||
3 |
Интерполирование функций: Интерполяционный многочлен Лагранжа |
||||||||||||||||||||||||||||||||||||||
3.1 |
График функции проходит через точки
Тогда её интерполяционный многочлен второго порядка равен: |
А) В) С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение: Способ1 Подставим значения х в многочлен Р(1)=1-3+5=3 р(2)=4-6+5=3 Р(3)=9-9+3=3 Подставим значения х в многочлен) Р(1)=1-1+3=3 р(2)=4-2+3=5 Р(3)=9-3+3=9 Подставим значения х в многочлен Р(1)=1-2+4=3 р(2)=4-4+4=4 Р(3)=9-6+4=7 После подстановки значений х в многочлен получили Р(1)=у1=3 Р(2)=у2=4 Р(3)=у3=7 ответ Способ2
|
||||||||||||||||||||||||||||||||||||||
3.2 |
График функции проходит через точки
Тогда её интерполяционный многочлен второго порядка равен |
А) В) С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение: Подставим значения х в многочлен Р(1)=0-2=-2 р(2)=4+8-2=10 Р(3)=9+12-2=19 Подставим значения х в многочлен Р(1)=0- Подставим значения х в многочлен Р(1)=-2
р(2)= Подставим значения х в многочлен Р(1)=0-2=-2 р(2)=4-2=2 Р(3)=6-2=4 После подстановки значений х в многочлен получили Р(1)=у1=-2 Р(2)=у2=2 Р(3)=у3=4 Ответ: |
||||||||||||||||||||||||||||||||||||||
3.3 |
Интерполяционный многочлен Лагранжа второй степени Р(х)= |
А)
В)
С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение: Подставим значения х в многочлен Р(х)= Р(-2)=4+1-1=4 Р(0)==-1 Р(2)=4-1-1=2 После подстановки значений х в многочлен получили Р(-2)=у1=4 Р(0)=у2=-1 Р(2)=у3=2 Ответ:
|
||||||||||||||||||||||||||||||||||||||
3.4 |
Функция представлена таблицей
Тогда значение f(-1), вычисленное с помощью интерполяционного многочлена Лагранжа, равно |
А) - 2 В) - 4 С) 4 D) - 3
|
|||||||||||||||||||||||||||||||||||||
|
Решение. Р(х)=
Р(-1)=-1-3= - 4 |
||||||||||||||||||||||||||||||||||||||
3.5 |
Функция представлена таблицей
Тогда значение f(-1), вычисленное с помощью интерполяционного многочлена Лагранжа, равно: |
А) 2 В) 1 С) 6 D) 3
|
|||||||||||||||||||||||||||||||||||||
|
Решение. Р(х)=3 Р(-1)=1-4+6=3 |
||||||||||||||||||||||||||||||||||||||
3.6 |
Интерполяционный многочлен Лагранжа второй степени Р(х)= |
А)
В)
С)
D)
|
|||||||||||||||||||||||||||||||||||||
|
Решение.Подставим значения х в многочлен Р(х)= Р(2)=8-18+9=-1 Р(3)=18-27+9=0 Р(4)=32-36+9=5 После подстановки значений х в многочлен получили Р(2)=у1=-1 Р(3)=у2=0 Р(4)=у3=5 Ответ:
|
||||||||||||||||||||||||||||||||||||||









 =0
принадлежит интервалу:
=0
принадлежит интервалу:











 на отрезке
на отрезке
 требуют последовательного вычисления
значения функции
требуют последовательного вычисления
значения функции
 в точках:
в точках:










 =0
принадлежит интервалу
=0
принадлежит интервалу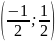



 =0
принадлежит интервалу:
=0
принадлежит интервалу:
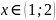
 на отрезке
требуют последовательного вычисления
значения функции
на отрезке
требуют последовательного вычисления
значения функции
 в точках:
в точках:



 не
подходит
не
подходит

 в точке
можно вычислить по формуле:
в точке
можно вычислить по формуле:
 ;
; ;
;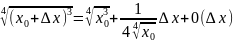 ;
;
 ;
; ;
;





 с использованием приближённой формулы
с использованием приближённой формулы


 =65 x0
=64
=65 x0
=64
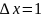

 c
использованием формулы
c
точностью до 0,01 равно
c
использованием формулы
c
точностью до 0,01 равно










 =-1,01 у0
=-1
=-1,01 у0
=-1

 =
=


 =
=















 x0
=1
x0
=1

 с точностью до 0,1 равно
с точностью до 0,1 равно

 с точностью до 0,01 равно
с точностью до 0,01 равно

 по формуле прямоугольников можно
найти:
по формуле прямоугольников можно
найти:



 точками
точками
 на n
равных частей длины
на n
равных частей длины

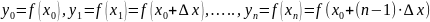



















 =-
р(2)=
=-
р(2)= Р(3)=11-
Р(3)=11-
 Р(3)=24-0,75-2=21,25
Р(3)=24-0,75-2=21,25 может быть составлен по таблице
значений функции у=у(х):
может быть составлен по таблице
значений функции у=у(х):

 может быть составлен по таблице
значений функции у=у(х):
может быть составлен по таблице
значений функции у=у(х):