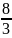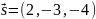- •Математика
- •Общие указания по подготовке к фэпо
- •Основная литература
- •Дополнительная литература
- •Электронные ресурсы
- •Раздел 1. Алгебра и геометрия
- •1. Определители
- •2. Матрицы
- •3. Векторная алгебра
- •Раздел 2. Математический анализ
- •Раздел 3. Дифференциальные уравнения
- •Раздел 4. Теория функций комплексного переменного.
- •Раздел 5. Теория вероятностей.
- •Раздел 6. Численные методы
- •2.Графический способ
- •1 Численные методы решения алгебраических уравнений
- •Раздел 7. Дискретная математика и абстрактная алгебра
- •664074, Иркутск, Лермонтова, 83
3. Векторная алгебра
Понятие вектора. Основные операции над векторами.
 -трёхмерное
декартово пространство;
-трёхмерное
декартово пространство;
 – двумерное декартово пространство –
плоскость;
– двумерное декартово пространство –
плоскость;
 - одномерное декартово пространство –
прямая.
- одномерное декартово пространство –
прямая.
Вектором
называется направленный отрезок прямой.
Обозначается
 ,
А – начало, В – конец вектора, или
,
А – начало, В – конец вектора, или
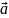 .
.
Длинавектора
– это его модуль, абсолютная величина,
обозначается
 ,
,
 .
.
Вектор называется нулевым, если его начало и конец совпадают.
В екторы
называются коллинеарными
(обозначается
екторы
называются коллинеарными
(обозначается
 ),
если они лежат на одной, либо на
параллельных прямых, их можно всегда
представить:
),
если они лежат на одной, либо на
параллельных прямых, их можно всегда
представить:

В екторы
называются компланарными,
если они лежат в одной, либо в параллельных
плоскостях.
екторы
называются компланарными,
если они лежат в одной, либо в параллельных
плоскостях.
Два вектора называются равными, если
1) коллинеарны,
2) имеют одинаковое направление,
3) имеют равные длины.

С уммой
уммой
 двух
векторов называют вектор, выходящий из
начала первого в конец второго, при
условии, что начало
двух
векторов называют вектор, выходящий из
начала первого в конец второго, при
условии, что начало
 совпадает
с концом
.
совпадает
с концом
.
Суммой
нескольких
векторов называется вектор, который
замыкает ломаную, составленную из
векторов слагаемых
 .
.
Правило параллелограмма
Е сли
векторы
и
приложены к общему началу и на них
построен параллелограмм, то сумма этих
векторов
представляет собой вектор, направленный
по диагонали, выходящей из общего начала,
а разность
сли
векторы
и
приложены к общему началу и на них
построен параллелограмм, то сумма этих
векторов
представляет собой вектор, направленный
по диагонали, выходящей из общего начала,
а разность
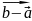 направлена по второй диагонали, причём
вектор разности направлен в сторону
уменьшаемого.
направлена по второй диагонали, причём
вектор разности направлен в сторону
уменьшаемого.
Произведениемвектора на вещественное число называется вектор , удовлетворяющий условиям:
1) коллинеарен вектору ;
2)

3 )
векторы
и
направлены одинаково, если
)
векторы
и
направлены одинаково, если
 и противоположны, если
<
0 , если же
=0
, то
=
0 .
и противоположны, если
<
0 , если же
=0
, то
=
0 .
Ортогональной
проекцией
вектора
на ось
 называется величина отрезка А’B’
оси.
называется величина отрезка А’B’
оси.
Обозначается:
 .
.
Теорема.
Проекция
вектора
на ось
равна длине вектора, умноженной на
косинус угла между вектором и осью .
.
Координатами вектора являются проекции вектора на оси координат.
Пусть
 тогда длина
(модуль) вектора
равна
тогда длина
(модуль) вектора
равна
 .
.
Рассмотрим
вектор
 где А(
где А( и В (
и В ( ,
тогда модуль
вектора
,
тогда модуль
вектора

Если
 – углы, образованные вектором с осями
координат, то имеет место равенство
– углы, образованные вектором с осями
координат, то имеет место равенство

Условие коллинеарности векторов в координатной форме
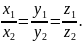
Вектор единичной длины, имеющий направление вектора , называется его ортом и обозначается

Скалярным произведением векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними

Работа равна скалярному произведению векторов силы и пути

Свойства скалярного произведения
1.
(
 следует из определения;
следует из определения;
2.
( ;
;
3.
(
 = (
= (
 ;
;
4.Если
 ,
так как
,
так как
 ;
;
5.
(
 0
0 (
(
 2
или
2
или
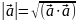
6.
(
 =
=

7.
(
 )
=
)
=

Скалярное произведение двух векторов в координатной форме

Условие перпендикулярности векторов
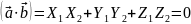
Векторным
произведением
вектора
на вектор
называется вектор
 ,
который удовлетворяет 3- м условиям:
,
который удовлетворяет 3- м условиям:
1)
 ;
;
2)
Вектор
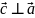 и
и
 ;
;
3) Вектор направлен так, что образует правую тройку с векторами и .
Обозначается или
или
 .
.
М одуль
векторного произведения
равен площади параллелограмма,
построенного на векторах-сомножителях.
одуль
векторного произведения
равен площади параллелограмма,
построенного на векторах-сомножителях.

Координатная форма векторного произведения

где = { X1 , Y1 Z1 } ; = { X2 ,Y2 ,Z2 }
С мешанным
произведением 3-х
векторов
мешанным
произведением 3-х
векторов
 ,
, называется скалярное произведение
вектора [
называется скалярное произведение
вектора [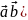 на вектор
,
([
на вектор
,
([ .
Обозначается: (
.
Обозначается: ( или (
или (
Смешанное
произведение векторов с точностью до
знака равно объёму параллелепипеда,
построенного на векторах сомножителях
 .
.
Пустьвектор = { X1 , Y1Z1 } ; вектор = { X2 ,Y2 ,Z2 } ; вектор = {X3 ,Y3 ,Z3 }.
Координатная форма смешанного произведения

Условием компланарности векторов является равенство нулю их смешанного произведения

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Полярная система координат
Полярная система координат состоит из начала точки О, называемой полюсом и лучом ОМ , соединяющем полюс с произвольной точкой М плоскости.

 –полярный
радиус-вектор
точки, угол
–полярный
радиус-вектор
точки, угол
 ,
образованный лучом ОМ и полярной осью
- полярный
угол точки.
Угол
считается
положительным при отсчёте от полярной
оси против часовой стрелки.
,
образованный лучом ОМ и полярной осью
- полярный
угол точки.
Угол
считается
положительным при отсчёте от полярной
оси против часовой стрелки.
Если
точка М имеет полярные координаты
 и
и
 то ей же отвечает и бесчисленное множество
пар полярных координат (
то ей же отвечает и бесчисленное множество
пар полярных координат ( и [-
и [- .
.
Если
начало декартовой прямоугольной системы
координат совместить с полюсом, а ось
Оx
направить по полярной оси, то прямоугольные
координаты x
и y
точки М и её полярные координаты
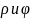 будут связаны следующими формулами:
будут связаны следующими формулами:
 ,
,
 ,
,
 .
.
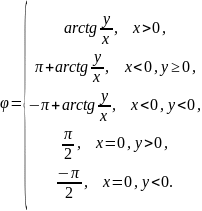
Различные виды уравнения прямой на плоскости
 -
общее уравнение прямой.
-
общее уравнение прямой.
1) С=0, Ax+By=0 - прямая проходит через начало координат.
2) B=0, Ax+C =0 - прямая параллельна оси оy.
3) A=0, By+C =0 - прямая параллельна оси ox.
4) B=C=0, Ax=0 , x=0 - ось oy.
5) А=С=0, Вy =0, y=0 - ось оx.
 -уравнение
прямой в отрезках,
a
и b
отрезки, отсекаемые прямой от осей
координат соответственно оx,
оy.
-уравнение
прямой в отрезках,
a
и b
отрезки, отсекаемые прямой от осей
координат соответственно оx,
оy.
 -каноническое
уравнение
прямой.
-каноническое
уравнение
прямой.
Вектор
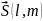 коллинеарный
прямой, называется направляющим
вектором
прямой.
коллинеарный
прямой, называется направляющим
вектором
прямой.
1)
Если
 то
то
 прямая параллельна оси оy.
прямая параллельна оси оy.
2)
Если m=0,
то
 прямая параллельна оси оx.
прямая параллельна оси оx.
Введя
обозначения
 ,
получим
,
получим
 -параметрические
уравнения
прямой.
-параметрические
уравнения
прямой.
 -уравнение
прямой, проходящей
через две точки.
-уравнение
прямой, проходящей
через две точки.
 -уравнение
прямой с
угловым коэффициентом, проходящей
через заданную точку.
-уравнение
прямой с
угловым коэффициентом, проходящей
через заданную точку.
 -
уравнение
прямой с угловым
коэффициентом, где
b
отрезок, который прямая отсекает от оси
ординат.
-
уравнение
прямой с угловым
коэффициентом, где
b
отрезок, который прямая отсекает от оси
ординат.
Взаимное расположение прямых на плоскости
 -
угол между двумя прямыми.
-
угол между двумя прямыми.
 -
угол между двумя прямыми.
-
угол между двумя прямыми.
 -
условие перпендикулярности прямых.
-
условие перпендикулярности прямых.
 -
условие перпендикулярности.
-
условие перпендикулярности.
 -
условие параллельности прямых.
-
условие параллельности прямых.
 -
условиепараллельности.
-
условиепараллельности.
 -
расстояние
от точки до прямой.
-
расстояние
от точки до прямой.
Кривые второго порядка
Кривой
второго порядка называется линия,
определяемая уравнением второй степени
A
1 )
Окружность
–
геометрическое место точек равноудалённых
от одной точки, называемой центром.
)
Окружность
–
геометрическое место точек равноудалённых
от одной точки, называемой центром.
Каноническое уравнение окружности
 -центр
окружности,
-центр
окружности,
r – радиус окружности
2) Эллипс - множество точек плоскости, сумма расстояний каждой из которых от 2-х данных точек этой плоскости, называемых фокусами, есть величина постоянная (при условии, что эта величина больше расстояния между фокусами).

 каноническое
уравнение эллипса,
каноническое
уравнение эллипса,
где
 ;
2b
– малая
ось;
2
;
2b
– малая
ось;
2 – большая
ось.
– большая
ось.
 эксцентриситет
эллипса.
эксцентриситет
эллипса.
3) Гипербола– геометрическое место точек, абсолютная величина разности расстояний каждой из которых от 2-х данных точек, называемых фокусами, есть величина постоянная (при условии, что эта величина не равна нулю и меньше расстояния между фокусами).

 –
каноническое
уравнение гиперболы, где
–
каноническое
уравнение гиперболы, где
 ;
;
2b
– мнимая
ось;
2
– действительная
ось.
 - асимптоты
гиперболы;
- асимптоты
гиперболы;
 – эксцентриситет
гиперболы.
– эксцентриситет
гиперболы.
 4)
Парабола–
множество точек, равноудалённых от
данной точки, называемой фокусом
и данной прямой, называемой директрисой
(фокус
не лежит на директрисе).
4)
Парабола–
множество точек, равноудалённых от
данной точки, называемой фокусом
и данной прямой, называемой директрисой
(фокус
не лежит на директрисе).
 – каноническое
уравнение
параболы.
– каноническое
уравнение
параболы.
Если
уравнение параболы имеет вид
 ,
то парабола симметрична относительно
оси оy,
а уравнение директрисы
,
то парабола симметрична относительно
оси оy,
а уравнение директрисы
 .
.
Различные виды уравнения плоскости в
 -
уравнение
плоскости через заданную точку.
-
уравнение
плоскости через заданную точку.
 общее
уравнение
плоскости.
общее
уравнение
плоскости.
Неполные уравнения плоскости
В общем уравнении полагаем:
1) D = 0,Ax + By + Cz = 0 , плоскость проходит через начало координат.
2) A = 0,By + Cz + D = 0 , плоскость параллельна оси ox.
A =D =0,By +Cz =0, плоскость проходит через ось ox.
3) В = 0,Аx +Cz +D = 0 , плоскость параллельна оси оy.
B =D = 0,Ax + Cz = 0, плоскость проходит через ось оy.
4) C = 0,Ax + By + D = 0 , плоскость параллельна оси oz.
C = D =0,Ax + By = 0, плоскость проходит через ось oz.
5) А = В =0,Сz + D = 0 , плоскость параллельна координатной плоскости XOY.
6) A =C = 0,By + D = 0 , плоскость параллельна координатной плоскости XOZ.
7) B = C = 0,Ax + D = 0, плоскость параллельна координатной плоскости YOZ.
8) A =B = D = 0,Cz = 0 или z = 0 , координатная плоскость XOY.
9) B =C = D = 0,Ax = 0 или x = 0 , координатная плоскость YOZ.
10) А = С = D = 0,By = 0 , координатная плоскость XOZ.
 -
уравнение плоскости в
отрезках,
где a,
b,
c-отрезки,
которые плоскость отсекает от осей
координат.
-
уравнение плоскости в
отрезках,
где a,
b,
c-отрезки,
которые плоскость отсекает от осей
координат.
 -
уравнение плоскости, проходящей через
три точки.
-
уравнение плоскости, проходящей через
три точки.
 -
нормальное уравнение плоскости , где
величина р
равна
ортогональной проекции радиуса вектора
фиксированной точки плоскости на
единичный вектор нормали.
-
нормальное уравнение плоскости , где
величина р
равна
ортогональной проекции радиуса вектора
фиксированной точки плоскости на
единичный вектор нормали.
Взаимное расположение плоскостей
- угол между плоскостями.
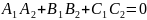 -
условие перпендикулярности плоскостей.
-
условие перпендикулярности плоскостей.
 -
условие параллельности плоскостей.
-
условие параллельности плоскостей.
 -
формула расстояния от точки до плоскости.
-
формула расстояния от точки до плоскости.
Прямая в пространстве
Линию
в пространстве рассматривают, как
множество всех точек, принадлежащих
двум пересекающимся поверхностям
 и
и

 -
общее
уравнение
прямой.
-
общее
уравнение
прямой.
 -
канонические
уравнения
прямой.
-
канонические
уравнения
прямой.
 -
параметрические уравнения
прямой.
-
параметрические уравнения
прямой.
 -
уравнение прямой, проходящей через
две точки.
-
уравнение прямой, проходящей через
две точки.
Взаимное расположение 2-х прямых
1)Угол
между двумя прямыми

2)
Условие параллельности
3)Условие
перпендикулярности

Взаимное расположение прямой и плоскости
1) Угол между прямой и плоскостью.


2)
Условие параллельности прямой и плоскости

3)
Условие перпендикулярности прямой и
плоскости

Контрольные задания к разделу №1
Определители |
||||||
1.1 |
Условие |
Варианты |
||||
Определитель
|
А) 6 В)-52 С)5 D)2 |
|||||
Решение
|
||||||
1.2 |
Условие |
Варианты |
||||
Определитель
|
А) -3 В)-1 С)0 D)-1 |
|||||
Решение
|
||||||
1.3 |
Условие |
Варианты |
||||
Определитель
|
А) 0 В)-3 С)2 D)-2 |
|||||
Решение
|
||||||
1.4 |
Условие |
Варианты |
||||
При
каких а обращается в нуль определитель |
А) 3 В)-3 С) D) |
|||||
Решение
|
||||||
1.5 |
Условие |
Варианты |
||||
Определитель
|
А) 30 В)-30 С)-2 D)2 |
|||||
Решение
|
||||||
1.6 |
Условие |
Варианты |
||||
Определитель
матрицы
|
А) 46 В)-46 С)-26 D)26 |
|||||
Решение
|
||||||
1.7 |
Условие |
Варианты |
||||
Формула
вычисления определителя третьего
порядка
|
А) ykn В)ykp С)ymn D)yzp |
|||||
Решение
|
||||||
Матрицы |
||||||
2.1 |
Условие |
Варианты |
||||
Произведение
матриц А= |
А)
В) С) D) |
|||||
Решение
|
||||||
2.2 |
Условие |
Варианты |
||||
Произведение
матриц
|
А) В) С) D) |
|||||
Решение
= |
||||||
2.3 |
Условие |
Варианты |
||||
Даны
матрицы А= |
А) -4 В) -2 С) 12 D) 6 |
|||||
Решение
|
||||||
2.4 |
Условие |
Варианты |
||||
Для
матрицы А= |
А) 2 В)4 С) -3 D) 5 |
|||||
Решение В=АТ= |
||||||
2.5 |
Условие |
Варианты |
||||
При
каком |
А) 2 В) 0 С)
D) 4 |
|||||
Решение Для вырожденной матрицы det A=0 det
|
||||||
2.6 |
Условие |
Варианты |
||||
Произведение матриц
|
А)
В) С) D)
|
|||||
Решение
|
||||||
2.7 |
Условие |
Варианты |
||||
Произведение
матриц с размерностью
|
А) m=2 k=3 В) m=1 k=2 С) m=3 k=1 D) m=2 k=1 |
|||||
Решение Матрицу А можно умножить на матрицу В, если число столбцов матрицы А равно числу строк матрицы В и получается матрица, у которой, столько строк сколько их имеет матрица - множимое и столько столбцов, сколько их имеет матрица - множитель. m=2k m=2 k=1 |
||||||
2.8 |
Условие |
Варианты |
||||
Матрица
А имеет размерность
|
А) , В) С) D) |
|||||
Решение Матрицу А можно умножить на матрицу В, если число столбцов матрицы А равно числу строк матрицы В и получается матрица, у которой, столько строк сколько их имеет матрица - множимое (А) и столько столбцов, сколько их имеет матрица - множитель (В). Матрица С будет иметь размерность |
||||||
2.9 |
Условие |
Варианты |
||||
Если
А=
|
А)
В) С) D) |
|||||
Решение
|
||||||
2.10 |
Условие |
Варианты |
||||
Если
А= |
А)
В) С) D) |
|||||
Решение
|
||||||
2.11 |
Условие |
Варианты |
||||
Дана
матрица А=
|
А)
В) С) D) |
|||||
Решение А2= |
||||||
2.12 |
Условие |
Варианты |
||||
Дана
матрица А= |
А)
В) С) D) |
|||||
Решение А2= |
||||||
2.13 |
Условие |
Варианты |
||||
Разность между числом базисных переменных и свободных переменных системы уравнений
|
А) 5 В) 1 С) 3 D) 4 |
|||||
Решение А= Rg=3
n-r=5-3=2
свободные переменные
разность 3-2=1 |
||||||
2.14 |
Условие |
Варианты |
||||
Ранг
матрицы
|
А) 0 В) 2 С) 4 D) 3 |
|||||
Решение Все строки линейно независимы. Rg=3 |
||||||
2.15 |
Условие |
Варианты |
||||
Ранг
матрицы
|
А) -6 В) 0 С) -18 D) 3 |
|||||
Решение
|
||||||
2.16 |
Условие |
Варианты |
||||
Матрица
|
А) 2 В) 0,5 С) 0 D) -2 |
|||||
Решение Матрица не имеет обратной, если det A=0
|
||||||
2.17 |
Условие |
Варианты |
||||
Ранг
матрицы
|
А) -5 В) 4 С) -7 D) 7 |
|||||
Решение
|
||||||
2.18 |
Условие |
Варианты |
||||
Матрица
|
А)
В)
С)
D)
|
|||||
Решение Матрица не имеет обратной, если det A=0
|
||||||
|
Векторы |
|||||
3.1 |
Условие |
Варианты |
||||
Даны
|
А) 4 В) 5 С) 3 D) -3 |
|||||
Решение ( Прох( |
||||||
3.2 |
Условие |
Варианты |
||||
Косинус
угла между векторами
|
А)
В) С) D)
|
|||||
Решение
|
||||||
3.3 |
Условие |
Варианты |
||||
Даны
точки А (1;0), В (-2; -4), С(1; - 4). Установите
соответствие между отрезком !)
2)
|
А) 5 В) 7 С) 4 D) 3 |
|||||
Решение
|
||||||
3.4 |
Условие |
Варианты |
||||
Точка В (6;-3) является серединой отрезка АС, где А (0;1). Тогда точка С имеет координаты |
А) (3; -1) В) (-5; 4) С) (12; -7) D) (6; -3) |
|||||
Решение ХВ=
|
||||||
3.5 |
Условие |
Варианты |
||||
Расстояние между точками А( -3; -1) и В (9;4) равно |
А) 13 В) 17 С) 5 D)
|
|||||
Решение
|
||||||
3.6 |
Условие |
Варианты |
||||
Векторы
|
А) 2 В) -1 С) 2,5 D) -2 |
|||||
Решение Если , так как ;
|
||||||
3.7 |
Условие |
Варианты |
||||
Векторы
|
А) 2.5 В) -0.5 С) -2,5 D) 0.5 |
|||||
Решение Если , так как ;
|
||||||
3.8 |
Условие |
Варианты |
||||
Векторы
|
А) 2 В) -2 С) 3 D) -3 |
|||||
Решение Векторы
компланарны, если
|
||||||
3.9 |
Условие |
Варианты |
||||
Если
|
А)
В) С) D) 0 |
|||||
Решение
|
||||||
3.10 |
Условие |
Варианты |
||||
Упрощение
выражения
|
А)
В) С)
D)
|
|||||
Решение
|
||||||
3.11 |
Условие |
Варианты |
||||
Упрощение
выражения
|
А)
В) С) 2 D)
|
|||||
Решение
|
||||||
3.12 |
Условие |
Варианты |
||||
Упрощение
выражения
|
А) В) С)
D)
|
|||||
Решение
=
|
||||||
3.13 |
Условие |
Варианты |
||||
Упрощение
выражения
|
А)
В) С)
D)
|
|||||
Решение
|
||||||
Аналитическая геометрия |
||||||
4.1 |
Условие |
Варианты |
||||
Точка
А
задана
в прямоугольной системе координат
|
А)
В) С) D) |
|||||
Решение
|
||||||
4.2 |
Условие |
Варианты |
||||
Точка
А |
А)
В) С) D |
|||||
Решение , .
|
||||||
4.3 |
Условие |
Варианты |
||||
Точка А задана в прямоугольной системе координат . Тогда её полярные координаты равны |
А)
В) С) D |
|||||
Решение , .
|
||||||
4.4 |
Условие |
Варианты |
||||
Точка
А(6;
|
А)
В) С) (5;30) D)
|
|||||
Решение
х=
|
||||||
4.5 |
Условие |
Варианты |
||||
Точка А(2; ) задана в полярной системе координат. Тогда в прямоугольной системе координат точка имеет вид |
А)
В) С)
D)
|
|||||
Решение
х=
|
||||||
4.6 |
Условие |
Варианты |
||||
Даны точки А (0;1) и С (6;-3) Тогда сумма координат середины отрезка АС равна |
А) 5 В) 19 С) 2 D) 4 |
|||||
Решение ХВ= УВ=
|
||||||
4.7 |
Условие |
Варианты |
||||
Полярное
уравнение окружности
|
А)
В) С) D) |
|||||
Решение
|
||||||
4.8 |
Условие |
Варианты |
||||
Радиус
окружности
|
А) 5 В) 4 С) 3 D) 2 |
|||||
Решение (
R=5 |
||||||
4.9 |
Условие |
Варианты |
||||
Радиус
окружности
|
А)
В) 1 С) 3 D) 2 |
|||||
Решение ( уравнение окружности
R=1 |
||||||
4.10 |
Условие |
Варианты |
||||
Расстояние
между центрами окружностей, заданных
уравнениями
|
А) 3 В) С) D) |
|||||
Решение Приведём
к каноническому виду уравнение первой
окружности
|
||||||
4.11 |
Условие |
Варианты |
||||
Расстояние
между фокусами эллипса
|
А) 10 В) 8 С) 12 D) 18 |
|||||
Решение
|
||||||
4.12 |
Условие |
Варианты |
||||
Какое
из уравнений определяет гиперболу
1)
2) |
А) 1 В) 2 С) 3 D) 4 |
|||||
Решение Уравнение гиперболы Следовательно 2 |
||||||
4.13 |
Условие |
Варианты |
||||
Расстояние
между фокусами гиперболы
|
А) 2 В) С) D) |
|||||
Решение
|
||||||
4.14 |
Условие |
Варианты |
||||
Если
уравнение окружности имеет вид
|
А) С(1;1) r=4 В) С(-1;-1) r=4 С) С(1;1) r=16 D)С(-1;-1) r=16 |
|||||
Решение ( уравнение окружности C(хо;уо)-центр окружности Следовательно С(1;1) r=4 |
||||||
4.15 |
Условие |
Варианты |
||||
Если
уравнение эллипса имеет вид
|
А) 5 В) 11 С) 25 D)
|
|||||
Решение a.b- полуоси
|
||||||
4.16 |
Условие |
Варианты |
||||
Если
уравнение эллипса имеет вид
|
А) 3 В) 9 С) 16 D)
|
|||||
Решение a.b- полуоси
|
||||||
4.17 |
Условие |
Варианты |
||||
Если
уравнение гиперболы имеет вид
|
А) 8 В) 15 С) 64 D)
|
|||||
Решение a.- действительная полуось
|
||||||
4.18 |
Условие |
Варианты |
||||
Острый угол между прямыми L1: 2х-у+4=0 и L2: - 3х-у+3=0 равен |
А) В) С) D) |
|||||
Решение
Следовательно, острый угол равен |
||||||
4.19 |
Условие |
Варианты |
||||
Синус
угла между прямой
|
А)
В) С) D) |
|||||
Решение
Направляющий
вектор прямой
Нормальный
вектор плоскости
|
||||||
4.20 |
Условие |
Варианты |
||||
Нормальный вектор плоскости х-4у-8z+3=0 имеет координаты |
А) (-4;-8;-3) В) (1; 4; 8) С) (1; -4; -8) D) (-3; -8; -3) |
|||||
Решение
Нормальный
вектор плоскости
|
||||||
4.21 |
Условие |
Варианты |
||||
Уравнение
прямой
|
А) 2х+3у=1 В) С) D) 3х+2у-4=0 |
|||||
Решение
|
||||||
4.22 |
Условие |
Варианты |
||||
Среди плоскостей 1) – х+2у+z-1=0 2) 3х+6у-9z-5=0 3) 2х+4у+6z-7=0 4) х-2у+z -7= 0 |
А) 1и4 В) 1и2 С) 3и4 D) 2и4 |
|||||
Решение Нормальные
векторы
Условием
ортогональности векторов является
|
||||||
4.23 |
Условие |
Варианты |
||||
Прямая
|
А) -1 В) -3 С) -9 D) 6 |
|||||
Решение
Направляющий
вектор прямой
Нормальный
вектор плоскости
Условие параллельности прямой и плоскости b – 6 + 15=0 b= - 9 |
||||||
4.24 |
Условие |
Варианты |
||||
В пространстве имеется отрезок, соединяющий две точки с аппликатами одинаковых знаков. Тогда этот отрезок не может пересекать |
А) плоскость ОХУ В) плоскость ОХZ С) плоскость ОУZ D) ось ординат |
|||||
Решение Отрезок не может пересекать плоскость ОХУ |
||||||
4.25 |
Условие |
Варианты |
||||
В пространстве имеется отрезок, соединяющий две точки с нулевыми абсциссами. Тогда этот отрезок целиком лежит в плоскости |
А) плоскости ОХУ В) плоскости ОХZ С) плоскости ОУZ D) на оси абсцисс |
|||||
Решение Отрезок лежит в плоскости ОУZ |
||||||
4.26 |
Условие |
Варианты |
||||
В пространстве имеется отрезок, соединяющий две точки с аппликатами разных знаков. Тогда этот отрезок обязательно пересекает |
А) плоскость ОХУ В) плоскость ОХZ С) плоскость ОУZ D) ось аппликат |
|||||
Решение Отрезок пересекает плоскость ОХУ |
||||||
4.27 |
Условие |
Варианты |
||||
Уравнение прямой, параллельной у=3х-1 является |
А) 3х - у+2=0 В) 3х+у-1=0 С) х+у-2=0 D) х-у-3=0 |
|||||
Решение Для прямой у=3х-1 к=3, для параллельных прямых к1=к2 3х - у+2=0 у=3х+2 к=3 следовательно прямые параллельны |
||||||
4.27 |
Условие |
Варианты |
||||
Уравнение
прямой, параллельной
|
А) 4х - у+2=0 В) 4х+у-1=0 С) х+у-2=0 D) х-у-3=0 |
|||||
Решение Для прямой х+4 к = - 1, для параллельных прямых к1=к2 х+у-2=0 х+2 к = - 1 следовательно прямые параллельны |
||||||
4.28 |
Условие |
Варианты |
||||
Уравнение
прямой, перпендикулярной
|
А) х +6у-7=0 В) 6х - у-2=0 С) х+5у-2=0 D) 5х-у -3=0 |
|||||
Решение - условие перпендикулярности прямых Для
прямой у = 6х-5
Для
х +6у-7=0
|
||||||
4.29 |
Условие |
Варианты |
||||
Если плоскость Ах+Ву +5z - 9=0 проходит через точку Т(2;-2;3), то А-В равно |
А) 0 В) -3 С) 2 D) -2 |
|||||
Решение Так как плоскость Ах+Ву +5z - 9=0 проходит через точку Т(2;-2;3), то 2А-2В+15-9=0 А-В= -3 |
||||||
4.30 |
Условие |
Варианты |
||||
Угловой коэффициент прямой 2х-4у+1=0 равен |
А) 2 В) -4 С) 0,5 D) -0,5 |
|||||
Решение Уравнение прямой с угловым коэффициентом 2х-4у+1=0 4у=2х+1 у=0,5х+0,25 к=0,5 |
||||||
4.31 |
Условие |
Варианты |
||||
Установить соответствие между уравнениями плоскостей и их расположением 1) 2х-3у+5z=0 2) 2z-3=0 3) -2у+3z+5=0 4) 4у+5z=0 |
А) проходит через ось ОУ В) проходит через ось ОХ С) параллельно плоскости ХОУ D)проходит через начало координат Е) параллельно оси ОХ |
|||||
Решение 2х-3у+5z=0 проходит через начало координат 2z-3=0 параллельно плоскости ХОУ -2у+3z+5=0 параллельно плоскости ХОУ 4у+5z=0 проходит через ось ОХ |
||||||
4.32 |
Условие |
Варианты |
||||
Прямая
|
А) -1 В)
- С) - D) 0 |
|||||
Решение
Направляющий
вектор прямой
Нормальный
вектор плоскости
Условие параллельности прямой и плоскости 4 +3к -4=0 b= 0 |
||||||
4.33 |
Условие |
Варианты |
||||
Общее уравнение прямой, проходящей через точки А(-2;3) В(3;-3) имеет вид |
А) 6х+5у-27=0 В) -5х+6у=0 С) -5х-у-7=4 D) 6х+5у-3=0 |
|||||
Решение уравнение прямой, проходящей через две точки
6х+12= - 5у+15 6х+5у-3=0 |
||||||
4.34 |
Условие |
Варианты |
||||
Установитьсоответствие между уравнениями прямых и их типами 1) у= - 3х+7 2) х= - 2 3)
|
А) уравнение параллельно оси абсцисс В) уравнение прямой с угловым коэффициентом С) уравнение прямой в отрезках D) общее уравнение прямой Е) уравнение прямой параллельно оси ОУ |
|||||
Решение у= - 3х+7 уравнение с угловым коэффициентом х= - 2 уравнение параллельно оси ОУ - уравнение прямой в отрезках |
||||||

 равен
равен
 равен
равен
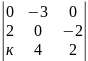 равен нулю при к равном
равен нулю при к равном




 равен
равен
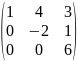 равен
равен
 содержит следующие произведения
содержит следующие произведения
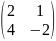 и В=
и В= равно
равно




 равно
равно



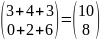
 В=
В=
 Сумма элементов матрицы ВА расположенных
на главной диагонали равна
Сумма элементов матрицы ВА расположенных
на главной диагонали равна ,
-1-4+3=-2
,
-1-4+3=-2 элемент в12
матрицы В=АТ
равен
элемент в12
матрицы В=АТ
равен в12=а21=4
в12=а21=4 матрица
матрица
 вырожденная
вырожденная


 и
и равно
равно




 и
и
 возможно при
возможно при
 ,
матрица В имеет размерность
,
матрица В имеет размерность
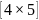 .
Тогда матрица С-=АВ будет иметь
размерность
.
Тогда матрица С-=АВ будет иметь
размерность ,
, ,
, ,
,
 В=
В= тогда матрица С=2А+В имеет вид
тогда матрица С=2А+В имеет вид




 и В=
и В= тогда С=А-2В имеет вид
тогда С=А-2В имеет вид



 -
- Тогда матрица А2
имеет вид
Тогда матрица А2
имеет вид




 .
Тогда матрица А2
имеет вид
.
Тогда матрица А2
имеет вид




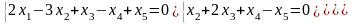 равна
равна

 -
базисные переменные,
-
базисные переменные,
 равен
равен равен двум при
равен двум при
 равном
равном
 не имеет обратной при
равном
не имеет обратной при
равном
 равен двум при
равном
равен двум при
равном ,
,
 не
имеет обратной, при
не
имеет обратной, при
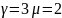




 Тогда проекция вектора (
Тогда проекция вектора ( )на
ось ОХ равна
)на
ось ОХ равна

 равен
равен
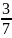




 ,
3)
,
3) и его длиной
и его длиной



 УВ=
УВ=
 Хс=12
Ус=
- 7
Хс=12
Ус=
- 7

 перпендикулярны при m равном
перпендикулярны при m равном m=2
m=2 перпендикулярны при m равном
перпендикулярны при m равном m=
- 2.5
m=
- 2.5 компланарны при m равном
компланарны при m равном
 4+2m=0
m= - 2
4+2m=0
m= - 2 ;
;
 тогда
угол векторами
тогда
угол векторами
 равен
равен



 приводит его к виду
приводит его к виду






 приводит
его к виду
приводит
его к виду





 приводит
его к виду
приводит
его к виду




 приводит
его к виду
приводит
его к виду





 .
Тогда её полярные координаты равны
.
Тогда её полярные координаты равны



 ,
.
,
.

 задана
в прямоугольной системе координат
.
Тогда её полярные координаты равны
задана
в прямоугольной системе координат
.
Тогда её полярные координаты равны
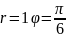







 )
задана в полярной системе координат.
Тогда в прямоугольной системе координат
точка имеет вид
)
задана в полярной системе координат.
Тогда в прямоугольной системе координат
точка имеет вид





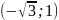




 ХВ=3
УВ=
- 1
ХВ=3
УВ=
- 1 имеет
вид
имеет
вид
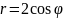




 равен
равен уравнение
окружности
уравнение
окружности

 равен
равен


 и
и
 равно
равно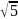

 Центр ревой окружности находится в
точке С(2;1), центр второй окружности в
точке О(0;0). Найдём расстояние между
точками О и С.
Центр ревой окружности находится в
точке С(2;1), центр второй окружности в
точке О(0;0). Найдём расстояние между
точками О и С.

 равно
равно

 3)
3)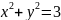 4)
4)
 равно
равно



 ,
то его центром С и радиусом r являются
,
то его центром С и радиусом r являются ,
то длина его большей полуоси равна
,
то длина его большей полуоси равна
 тогда
большая полуось равна 5
тогда
большая полуось равна 5 ,
то длина его меньшей полуоси равна
,
то длина его меньшей полуоси равна
 тогда
меньшая полуось равна 3
тогда
меньшая полуось равна 3 ,
то длина её действительной полуоси
равна
,
то длина её действительной полуоси
равна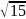
 тогда
действительная полуось равна 8
тогда
действительная полуось равна 8


 и плоскостью х-2у-3z+9=0
и плоскостью х-2у-3z+9=0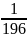




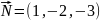
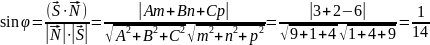

 имеет вид
имеет вид

 уравнение
в отрезках примет вид
уравнение
в отрезках примет вид



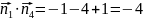

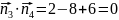

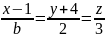 параллельна плоскости
параллельна плоскости
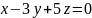 при b равном
при b равном

 х+4
является
х+4
является
 является
является


 параллельна плоскости
параллельна плоскости
 при к равном
при к равном