7.2. Прискорення точок тіла

На підставі формули (7.12) знайдемо закон розподілу прискорень у вільному твердому тілі. Диференціюємо рівність (7.12):

,

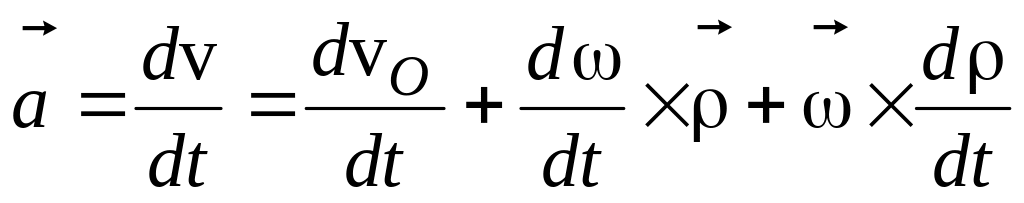(7.13)

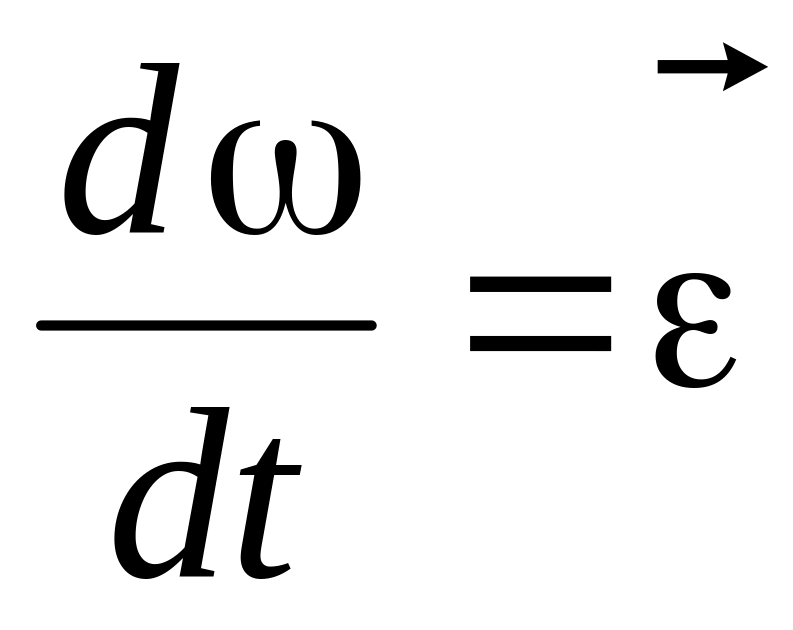де - прискорення полюса ; - кутове прискорення тіла; - швидкість точки відносно полюса (відмітимо, що диференціювання вектора здійснюється у рухомій системі координат, тому ).

Враховуючи ці позначення, будемо мати:

,

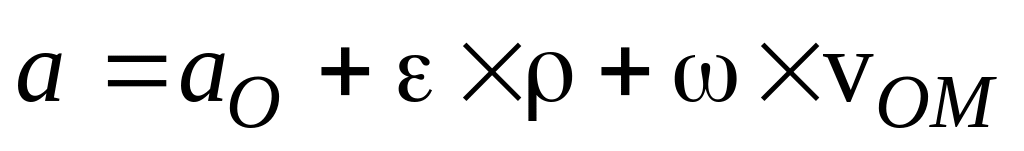(7.14)

де .

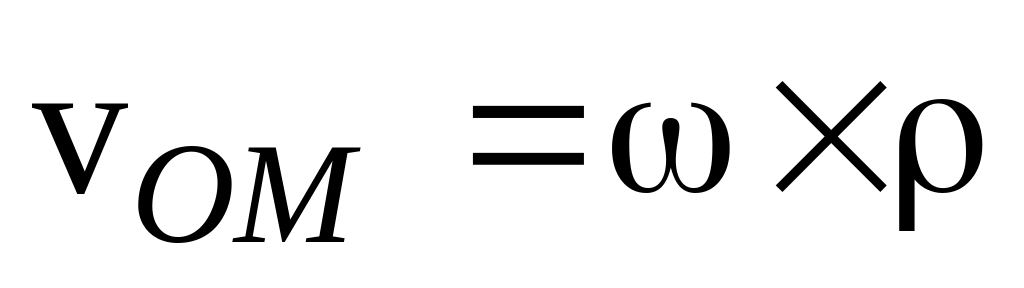Доданок називається обертальним прискоренням, а - доосьовим.

Взаємне розташування векторів і у формулі (7.14) стає конкретним у кожному частинному випадку руху:

обертання навколо нерухомої осі. і лежать на осі обертання (див. рис. 7.2).	плоскопаралельний рух. У цьому випадку вектори і є перпендикулярними до площини (див. рис. 7.3).
Рис. 7.2. Розташування векторів і при обертанні тіла навколо нерухомої осі.	Рис. 7.3. Розташування векторів і при плоскопаралельному русі тіла.

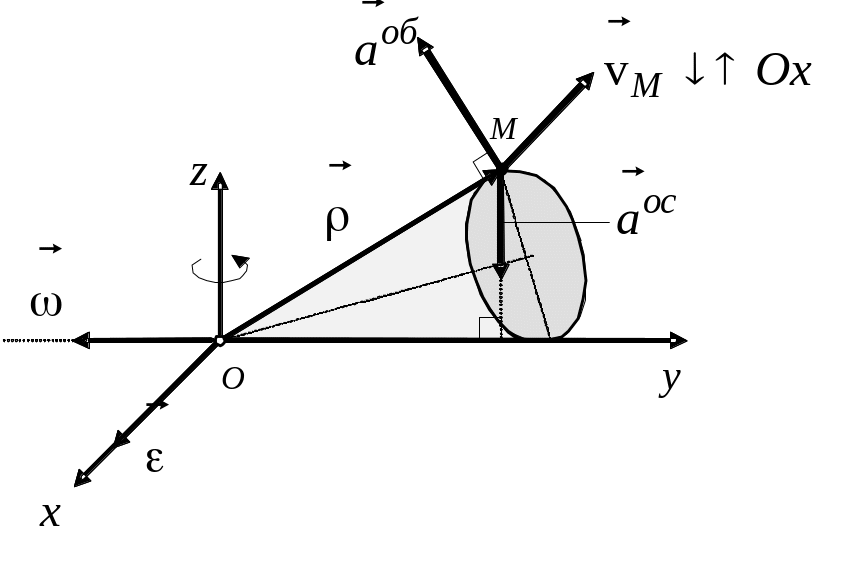
3. обертання твердого тіла навколо нерухомої точки (див. рис. 7.4)

Рис. 7.4. Розташування векторів і при обертанні тіла навколо нерухомої точки.

1 Лінія називається лінією вузлів.

49