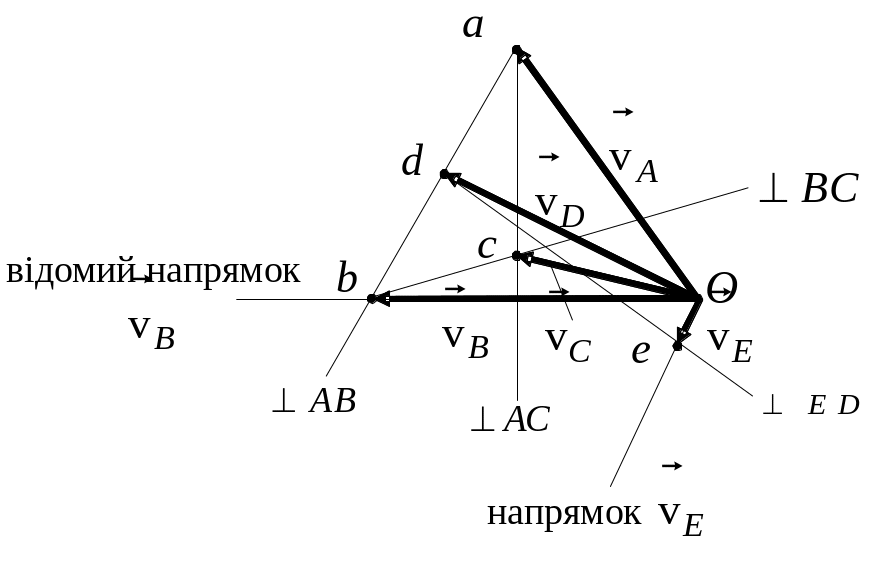5.4. План швидкостей
Планом швидкостей називається креслення, на якому графічним методом знаходяться швидкості всіх точок одного тіла або системи твердих тіл, що рухаються у площині.
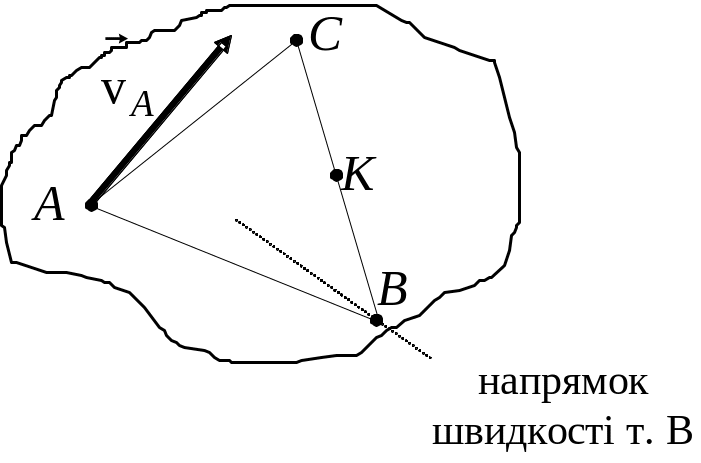
Знайдемо швидкості всіх точок твердого тіла. Отже, відома (задана) швидкість однієї точки за величиною і напрямком, а також відомий напрямок швидкості іншої точки (див. рис. 5.13).
Треба знайти швидкості всіх точок тіла.
Рис. 5.13. Постановка задачі. |
Виберемо за полюс т. , тоді
Рівність (5.11)
описує замкнений векторний трикутник,
в якому вектор
відомий повністю, а
і
Для цього із
довільного полюса
у масштабі будуємо відрізок
|
(рис. 5.13), а з полюса
- промінь за напрямком вектора швидкості
т.
![]() .
У трикутнику, що утворився:
.
У трикутнику, що утворився:
![]() .
.
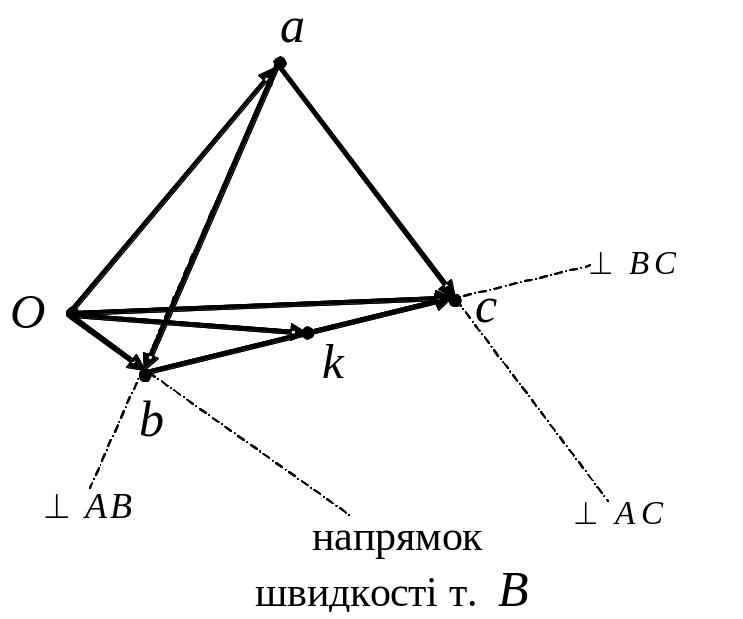
Рис. 5.14. План скоростей. |
Визначимо тепер
швидкість довільної
т.
де
відома повністю, а
де відомі напрямки
і
Зауважимо, що побудови на плані швидкостей відповідають графічному розв’язанню системи рівнянь (5.12)(5.13), тобто побудови |
![]() ,
призводять до:
,
призводять до:
![]() .
.
Приклад (побудови плану швидкостей системи твердих тіл).
Для механізму,
ланка
![]() якого обертається у додатному напрямку
з кутовою швидкістю
,
визначити графічно швидкості всіх його
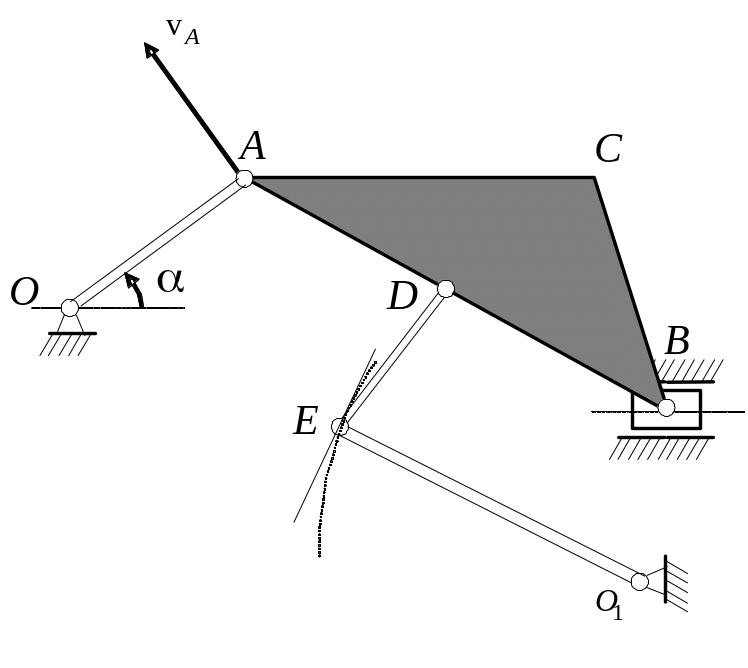
точок у положенні, схематично показаному
на рис. 5.15.
якого обертається у додатному напрямку
з кутовою швидкістю
,
визначити графічно швидкості всіх його
точок у положенні, схематично показаному
на рис. 5.15.
|
|
Рис. 5.15. Схема досліджуваного механізму. |
Рис. 5.16. План швидкостей для механізму з рис. 5.15. |
Послідовність побудови плану швидкостей така (див. рис. 5.16):
обчислюємо швидкість т. і будуємо вектор у масштабі від довільно вибраного полюса на плані швидкостей ( );
визначаємо швидкість т. (оскільки відомий її напрямок), користуючись формулою: , для чого через т. на плані швидкостей проводимо пряму
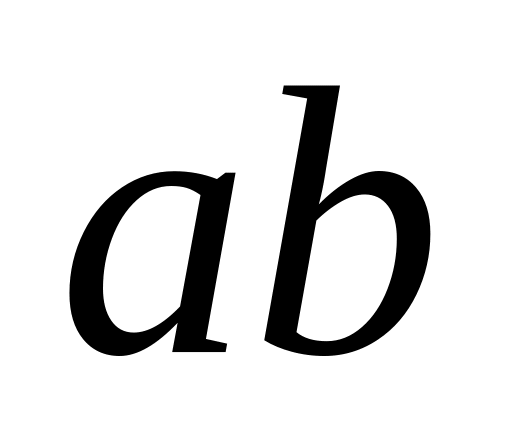 ,
перпендикулярну до відрізку
,
до перетину в т.
,
перпендикулярну до відрізку
,
до перетину в т.
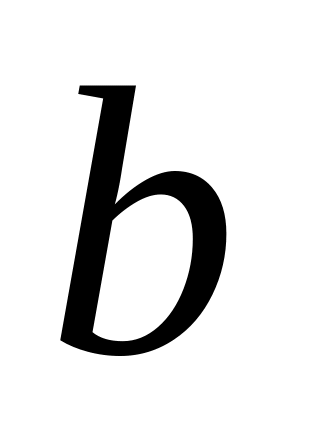 із відомим напрямком швидкості т.
,
проведеним із полюса
;
тоді
із відомим напрямком швидкості т.
,
проведеним із полюса
;
тоді
 ;
;для знаходження швидкості т. розв'язуємо графічно систему рівнянь
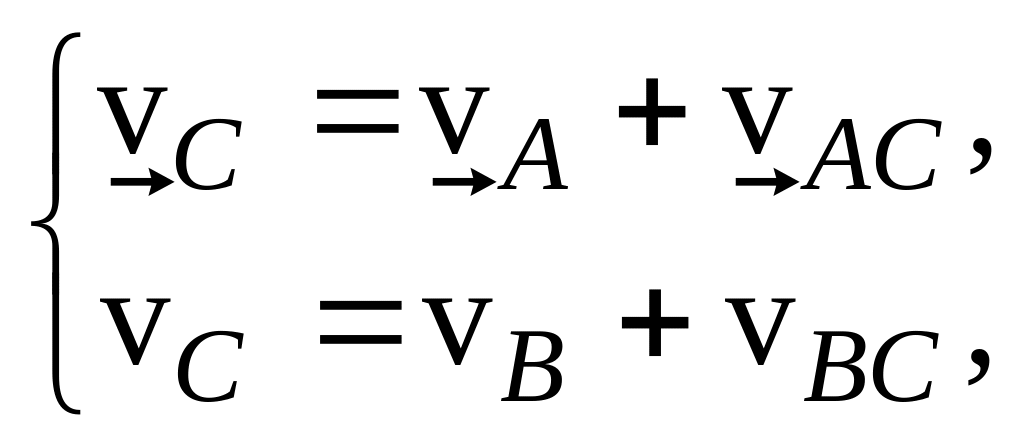 в
цьому випадку т.
в
цьому випадку т.
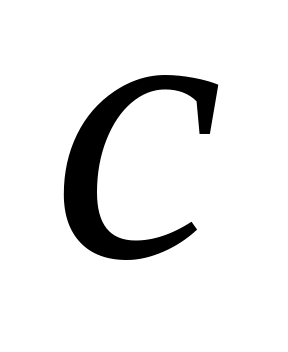 на плані швидкостей знаходиться як
перетин перпендикулярів до сторін
на плані швидкостей знаходиться як
перетин перпендикулярів до сторін
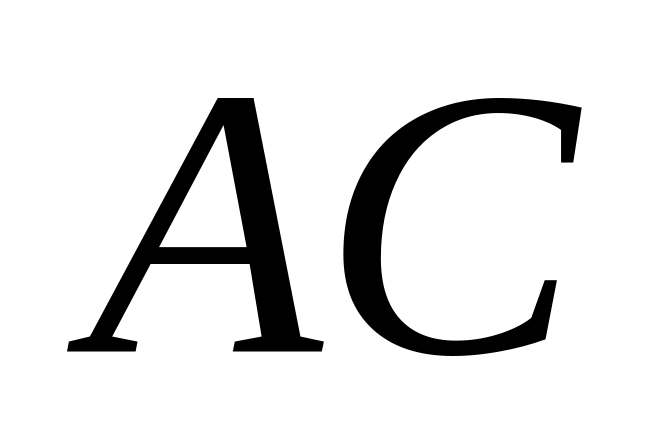 і
і
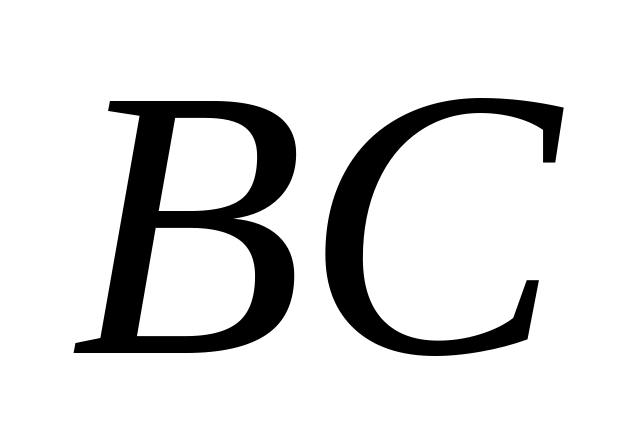 вихідного
вихідного
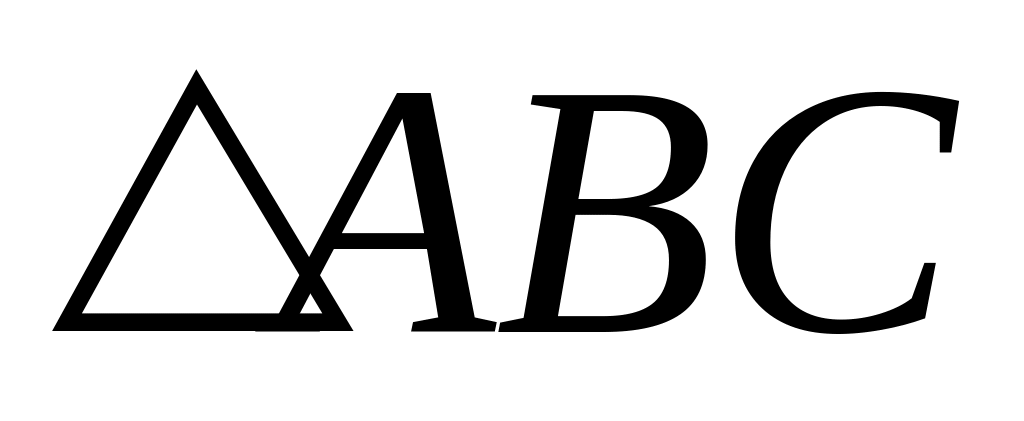 (тобто
(тобто
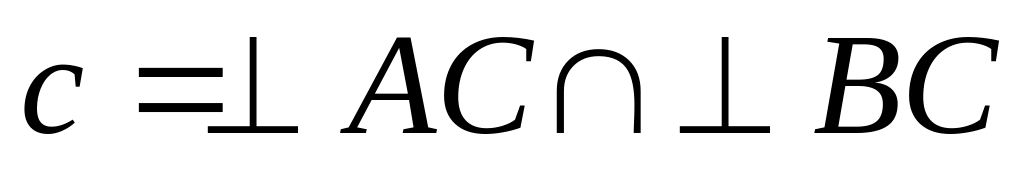 )
, і крім цього
)
, і крім цього
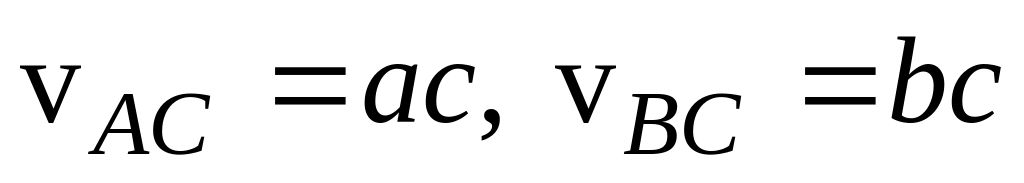 ;
отже,
;
отже,
 ;
;швидкість т.
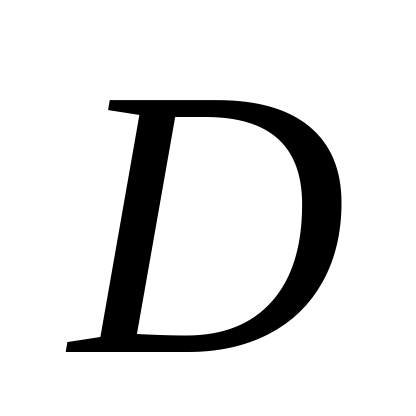 визначається із урахуванням того, що
ця точка ділить сторону
і відрізок
плану в однаковому відношенні (оскільки
побудови проводилися в одному масштабі),
тобто
визначається із урахуванням того, що
ця точка ділить сторону
і відрізок
плану в однаковому відношенні (оскільки
побудови проводилися в одному масштабі),
тобто
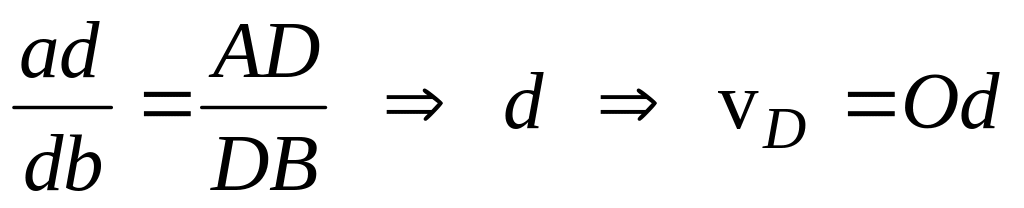 .
.знайдемо тепер швидкість т.
 .
Врахувавши те, що
.
Врахувавши те, що
 ,
проводимо
,
проводимо
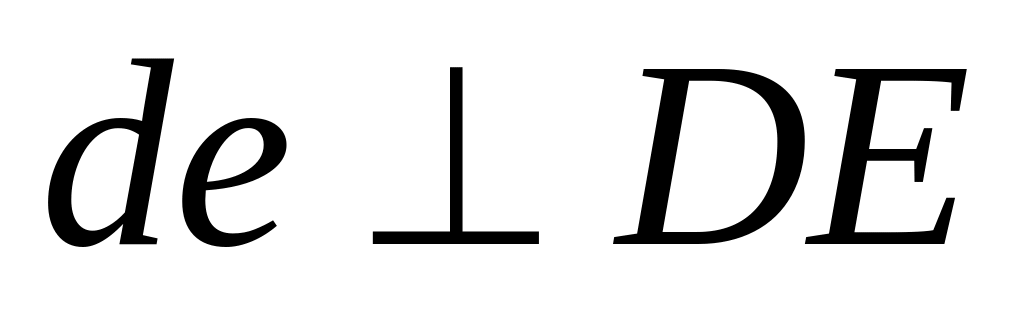 і з т.
пряму, що має напрямок швидкості
і з т.
пряму, що має напрямок швидкості
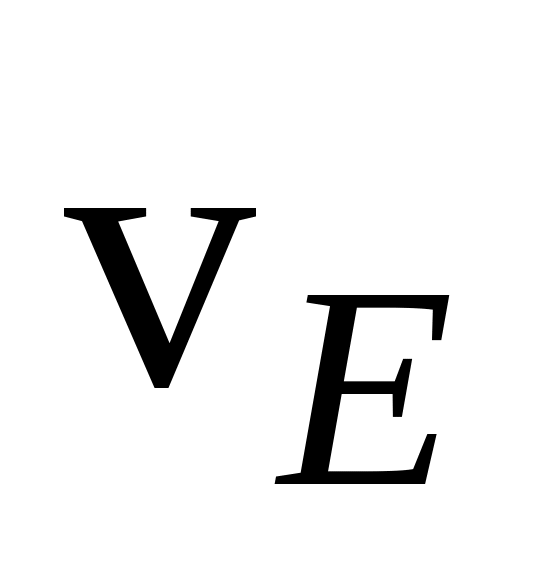 ;
отримуємо у перетині точку
;
отримуємо у перетині точку
 ,
тоді
,
тоді
 .
.