---------- Модуль НФ-07/1 «Кінематика і початок кінетики» ----------
Лекція 6
5. Плоскопаралельний (плоский) рух твердого тіла
Плоский рух твердого тіла – це такий рух тіла, під час якого всі точки тіла рухаються у площинах, паралельних деякій площині, нерухомій у розглядуваній системі відліку (основній площині).
Приклади тіл, що здійснюють плоский рух, вказані на рис. 5.1.
Рис. 5.1. Приклади тіл, що здійснюють плоский рух.
Покажемо, що вивчення плоскопаралельного руху (ППР) зводиться до вивчення руху незмінної плоскої фігури у нерухомій площині, що збігається із площиною цієї фігури.
Нехай
![]() -
основна площина, а тіло здійснює ППР,
тобто кожна точка тіла рухається
паралельно площині
(див. рис. 5.2). Спроектуємо т.
-
основна площина, а тіло здійснює ППР,
тобто кожна точка тіла рухається
паралельно площині
(див. рис. 5.2). Спроектуємо т.
![]() тіла на нерухому площину
,
-
тіла на нерухому площину
,
-
Рис. 5.2. До вивчення ППР. |
отримаємо т.
Таким чином, вивчення руху точки тіла зводиться до вивчення руху її проекції. Рух т. характеризує рух всіх точок, що лежать на перпендикулярі . Якщо всі точки тіла спроектувати на нерухому площину, то отримаємо плоску фігуру - проекцію тіла на нерухому площину. ППР тіла повністю визначається рухом його проекції на нерухому |
площину. Отже замість вивчення руху тривимірного тіла можна вивчати рух плоскої фігури.
5.1. Рівняння плоского руху
Складемо рівняння
руху плоскої фігури. Введемо нерухому
систему координат
![]() у площині фігури (див. рис. 5.3). Введемо
також жорстко зв'язану з фігурою с. к.
у площині фігури (див. рис. 5.3). Введемо
також жорстко зв'язану з фігурою с. к.
![]() ,
- положення тіла повністю визначається
положенням цієї с. к. А положення с. к.
відносно нерухомої
повністю визначається трьома параметрами:
,
- положення тіла повністю визначається
положенням цієї с. к. А положення с. к.
відносно нерухомої
повністю визначається трьома параметрами:
![]() .
.
Якщо кожному
моменту часу
![]() поставити у відповідність сукупність
параметрів (
),
то можна побудувати функції:
поставити у відповідність сукупність
параметрів (
),
то можна побудувати функції:
|
(5.1) |
|
(5.2) |
|
(5.3) |
|
Структура цих рівнянь показує, що рівняння (5.3) не залежить від (5.1) і (5.2), тобто:
характеристики
обертального руху під час ППР ( ППР являє собою синтез двох рухів: поступального і обертального навколо осі, перпендикулярної до основної площини і такої, що проходить через полюс. За полюс може бути вибрана довільна точка тіла. Для запису рівнянь руху окремої точки тіла слід скористатися формулами перетворення координат: |
![]() ;
;
![]() ,
,
або у матричній формі
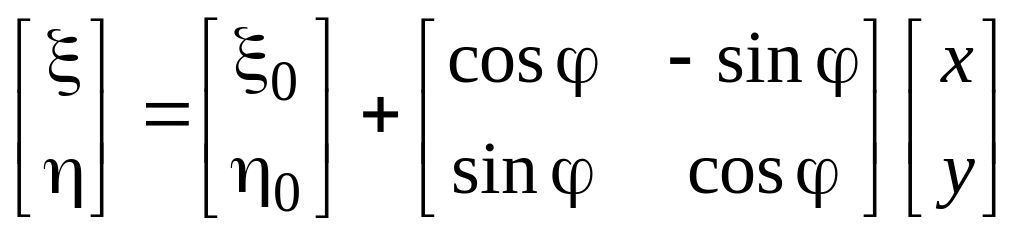 ,
або стисло:
,
або стисло:
![]() .
.
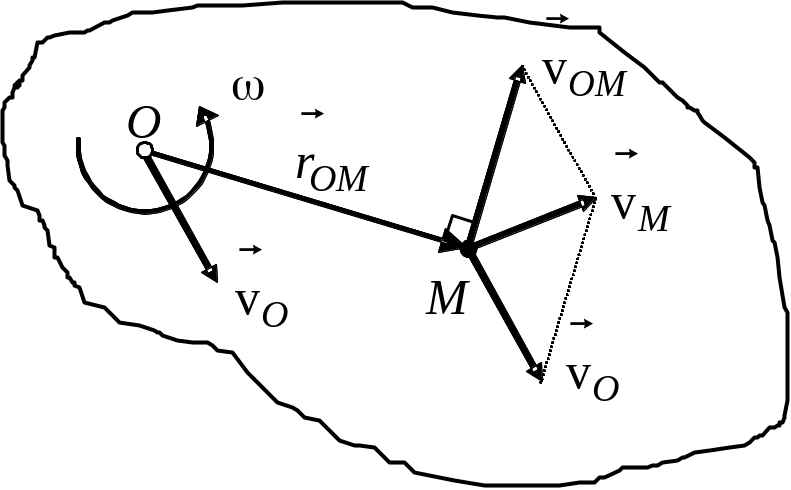
5.2. Теорема про розподіл швидкостей точок тіла
Визначимо швидкість
т.
цього тіла. Для цього введемо радіус-вектори
![]() ,
,
![]() ,
,
![]() ,
задаючи таким чином положення т.
в рухомій і нерухомій системах координат
(див. рис. 5.4).
,
задаючи таким чином положення т.
в рухомій і нерухомій системах координат
(див. рис. 5.4).
Рис. 5.4. Задання положення т. тіла в рухомій і нерухомій системах координат.
|
Розглянемо рух т. як складний. При цьому поступальний рух разом із полюсом є переносним, а обертальний навколо полюса – відносним. Із рисунка видно, що
але
(зауважимо, що
|
|
|||
. |
(5.5) |
||||
Визначимо швидкість . Оскільки відносний рух – обертальний, то за формулою Ейлера матимемо
|
(5.6) |
крім цього,
враховуючи, що вектор
![]() є завжди перпендикулярним до площини
фігури, а вектор
належить цій площині, то
є завжди перпендикулярним до площини
фігури, а вектор
належить цій площині, то
|
(5.7) |
а також
|
(5.8) |
що завжди виконується.
Рис. 5.5. До теореми про розподіл швидкостей. |
Геометричне представлення наведе-них вище формул показано на рис. 5.5. Таким чином, доведена наступна теорема про розподіл швидкостей: швидкість будь-якої точки тіла під час плоскопаралельного руху дорівнює векторній сумі швидкості полюса і швидкості обертального руху навколо полюса. Швидкість обертального руху навколо полюса є завжди перпендикулярною до прямої, що з'єднує точку з полюсом. |
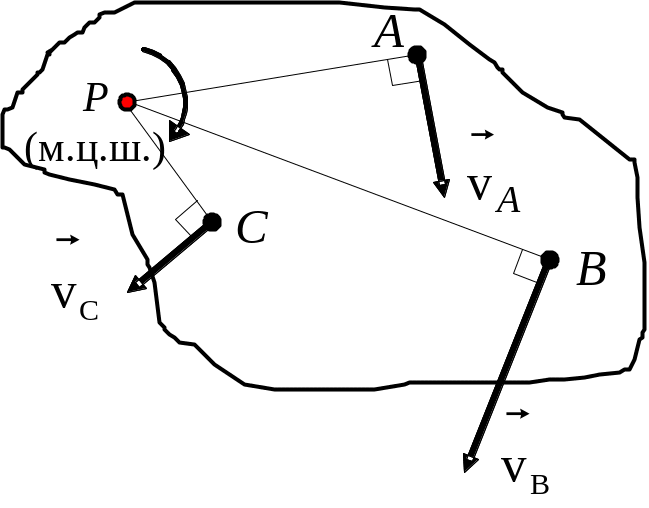
Наслідки:
1) проекції швидкостей двох точок тіла на пряму, що їх з’єднує, є рівними між собою (рис. 5.6). Це є кінематичне означення абсолютно твердого тіла.
Рис. 5.6. До наслідку 1. |
Для доведення
виберемо за полюс т.
спроектуємо цю
векторну рівність (5.9) на пряму
але
що і треба було довести; |
завжди існує точка, незмінно зв’язана (але необов'язково співпадаюча) з твердим тілом, швидкість якої у даний момент часу дорівнює нулю. Ця точка називається миттєвим центром швидкостей (м.ц.ш.).
Рис. 5.7. До наслідку 2. |
Якщо за полюс вибрати м.ц.ш., то закон розподілення швидкостей у тілі є законом розподілу швидкостей при обертальному русі, тобто тіло виконує миттєве обертання навколо осі, що проходить через м.ц.ш. (див. рис. 5.7).
|



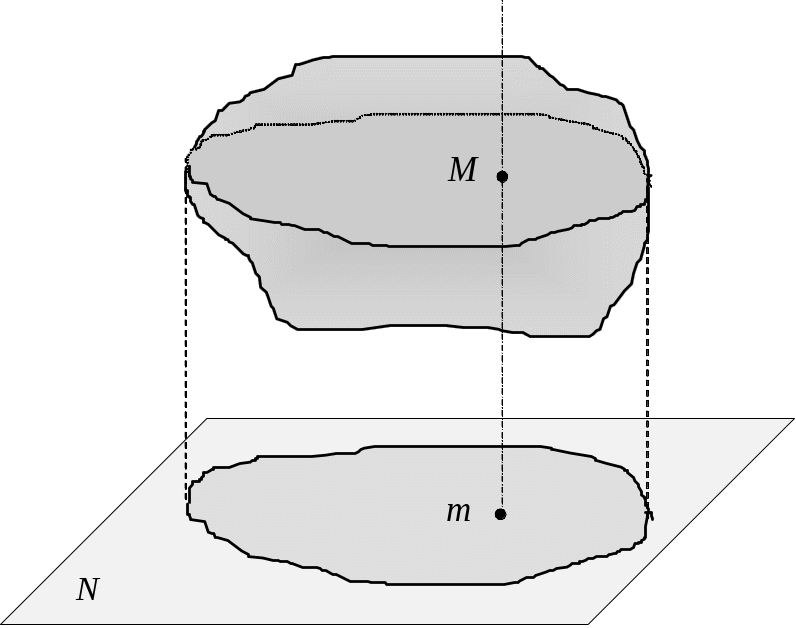
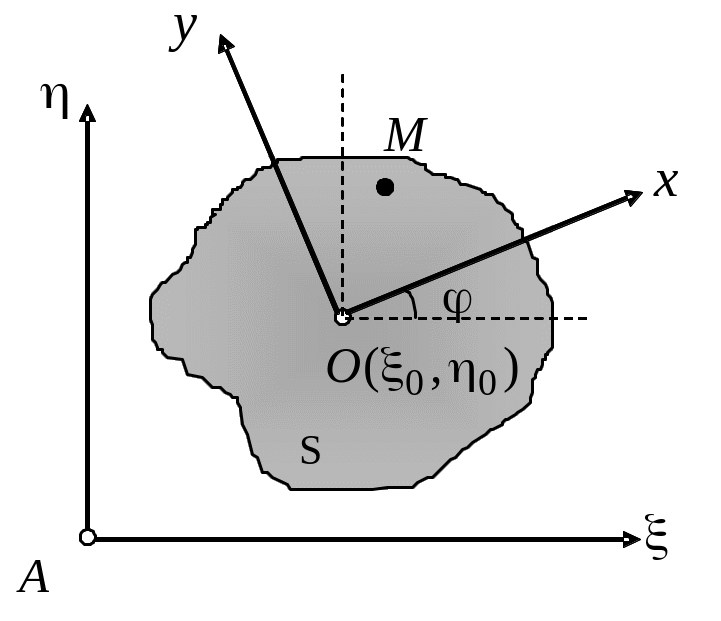 Рис. 5.3. До
задання ППР.
Рис. 5.3. До
задання ППР.