---------- Модуль НФ-07/1 «Кінематика і початок кінетики» ----------

Лекція 5

4. Синтез найпростіших рухів

Вище розглядалися найпростіші рухи твердого тіла. Однак тверде тіло може одночасно брати участь у кількох рухах, кожний з яких може виступати у вигляді комбінації найпростіших рухів. Вивченню найпростіших комбінацій рухів присвячений цей розділ. Зауважимо, що мова йтиме при синтез миттєвих поступальних і миттєвих обертальних рухів тіл, оскільки залежності між кінематичними характеристиками рухів вивчатимуться у кожний момент часу.

Поняття про абсолютний, відносний і переносний рухи точки, розглянуті у попередній лекції, можна поширити також на тверде тіло. Обмежимося в основному випадком, коли тверде тіло здійснює рух відносно двох систем координат (систем відліку), що рухаються одна відносно іншої.

4.1. Складання поступальних рухів

Теорема. При складанні поступальних рухів твердого тіла утворюється вислідний поступальний рух зі швидкістю, що дорівнює векторній сумі швидкостей складових рухів.

Д о в е д е н н я

Нехай відносний рух твердого тіла ІІ відносно тіла І буде поступальним зі швидкістю , а переносний рух тіла І і зв'язаної з ним с. к. щодо нерухомої буде також поступальним зі швидкістю (рис. 4.1).

Рис. 4.1. Складання поступальних рухів тіла.

Тоді абсолютна швидкість точки твердого тіла ІІ за теоремою про додавання швидкостей буде . (4.1) Оскільки абсолютні швидкості всіх точок тіла рівні між собою в кожний момент часу, то абсолютний рух твердого тіла буде поступальним, що і треба було довести. Одержану рівність можна узагальнити на випадок складання кількох миттєвих поступальних рухів. Більш того, якщо поступальний рух має місце на скінченному проміжку часу, то так само додаються і прискорення. Оскільки при поступальному русі на скінченному проміжку часу і коріолісове прискорення дорівнює нулю, то

отримаємо

.

(4.2)

Якщо швидкості всіх точок тіла виявляються рівними між собою лише у визначений момент часу, то рух є миттєво-поступальним. При цьому прискорення точок різні і їх не можна підсумовувати за формулою (4.2), бо у цьому разі, хоча кутова швидкість і дорівнює нулю, кутове прискорення може відрізнятися від нуля.

4.2. Складання обертань навколо осей, що перетинаються

Теорема. При складанні двох миттєвих обертань твердого тіла навколо перетинних осей утворюється вислідне обертання навколо миттєвої осі з кутовою швидкістю, що дорівнює векторній сумі кутових швидкостей складових обертань.

Д о в е д е н н я

Нехай тверде тіло ІІ одночасно обертається навколо двох перетинних осей. Навколо осі воно обертається разом із тілом І з кутовою швидкістю відносно нерухомої с. к. (рис. 4.2). Цей рух є переносним. Навколо осі тіло ІІ

Рис. 4.2. Складання обертань навколо перетинних осей.

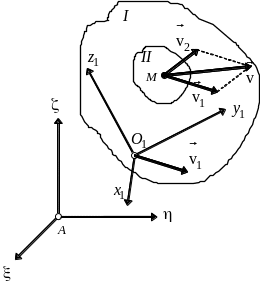
обертається відносно тіла І (і зв’язаної з ним с. к. ) з кутовою швидкістю , тобто це обертання є відносним. Потрібно знайти рух тіла ІІ відносно нерухомої с. к. . Точка залишається нерухомою, тому вислідний абсолютний рух тіла ІІ буде сферичним з деякою кутовою швидкістю , яку треба знайти за відомими кутовими швидкостями і складових обертань. Знайдемо абсолютну швидкість довільної точки тіла, задану радіусом-вектором , користуючись формулою (4.1): . Оскільки в кожній із введених систем координат радіус-вектор спільний, то з

попередньої формули дістанемо

.

(4.3)

Оскільки точка , а отже, і її радіус-вектор довільні, то

,

(4.4)

що і треба було довести.

Очевидно, що сукупність миттєвих обертань навколо перетинних в одній точці осей еквівалентна одному обертанню з миттєвою кутовою швидкістю:

.

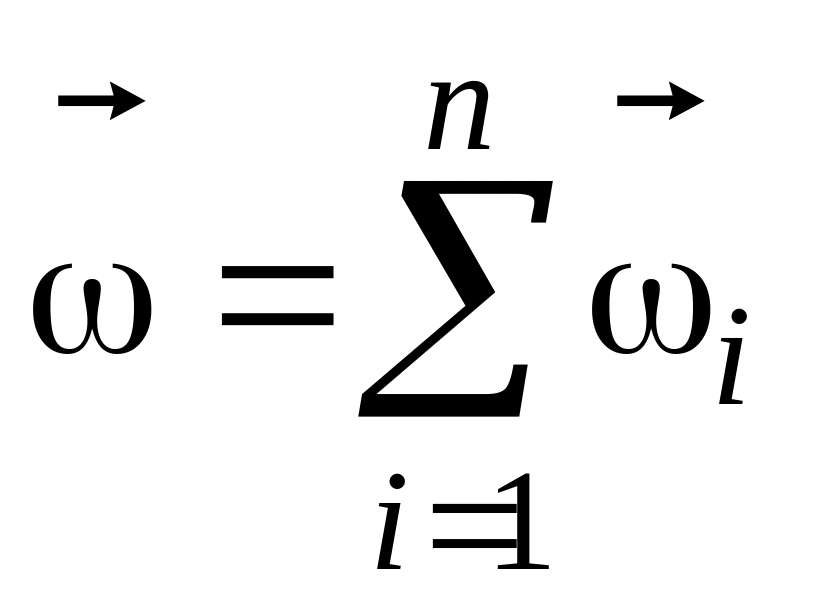Диференціювавши останнє співвідношення, одержимо формулу для додавання кутових прискорень:

.

Складання обертань навколо перетинних осей широко застосовується в техніці, а саме в різноманітних конічних та карданних передачах, планетарних редукторах, карданних підвісах, і т. п.