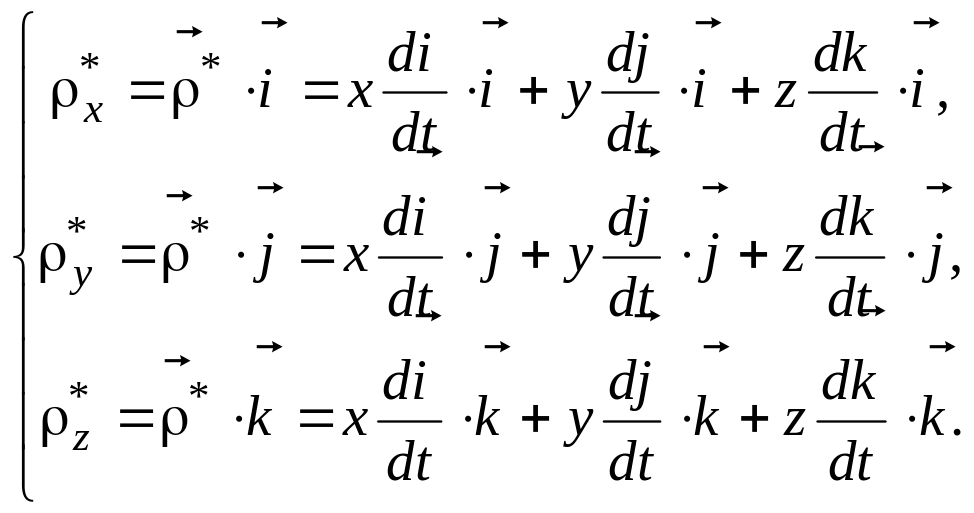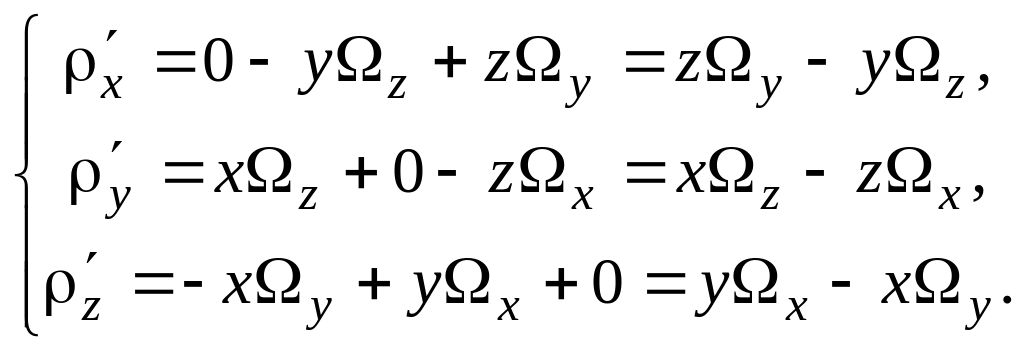---------- Модуль НФ-07/1 «Кінематика і початок кінетики» ----------

Лекція 4

3. Складний рух точки

3.1. Основні поняття

В класичній механіці прийняті умовно-нерухомі (інерціальні) системи відліку. Але в природі таких систем не існує, тому при розв'язуванні задач на практиці слід брати до уваги рухомість системи відліку.

Основною задачею кінематики складного руху точки є визначення основних його характеристик у двох різних системах координат (с. к.), якщо відомий взаємний відносний рух цих систем координат.

Введемо дві системи координат (див. рис. 3.1): умовно-нерухому с. к. - , і рухому с. к. - .

Рис. 3.1. Системи координат при складному русі точки.

Розглянемо рух точки , приймаючи до уваги рухомість с. к. . Назвемо рух т. відносно рухомої с. к. ( ) відносним, відносно нерухомої с. к. ( ) - абсолютним, і введемо поняття переносного руху (див. також рис. 3.2). Переносним рухом будемо називати рух тієї точки рухомого середовища, з якою у даний момент часу збігається рухома точка, відносно нерухомої системи координат.

Рис. 3.2. До визначення відносного, переносного і абсолютного рухів.

Визначимо положення т. у цих двох системах координат векторним способом.

Проведемо радіус-вектор із т. в т. . Тоді співвідношення

(3.1)

будемо називати кінематичним рівнянням відносного руху точки.

Положення т. у нерухомій с. к. визначається радіус-вектором , а положення початку рухомої с. к. відносно нерухомої - радіус-вектором .

3.2. Формула Бура

Розглянемо вираз вектора через його проекції в рухомій системі координат

	з ортами (рис. 3.3): , і знайдемо абсолютну похідну від нього . Оскільки система координат рухається довільним чином відносно , тому її одиничні вектори (орти) не є сталими, і вираз абсолютної похідної набуде вигляду
Рис. 3.3. До визначення вектора .
.		(3.2)

У формулі (3.2) перші три доданки характеризують зміну вектора в рухомій системі координат, тобто їх сума є відносною похідною

.

(3.3)

Останні три доданки у формулі (3.2) позначимо , тобто

.

(3.4)

Помножимо скалярно обидві частини виразу (3.4) послідовно на орти

(3.5)

Отримаємо деякі допоміжні співвідношення

;

.

Введемо наступні позначення:

,

(3.6)

тоді формули (3.5) набудуть вигляду

(3.7)

Ці вирази повністю збігаються з виразами проекцій векторного добутку на осі системи координат . Дійсно

.

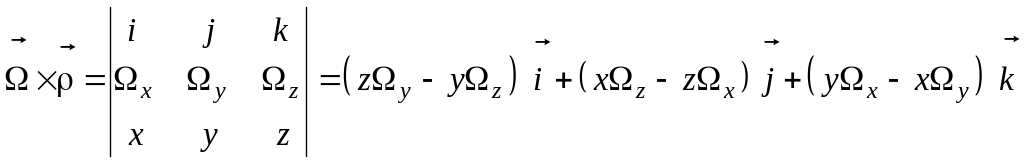Тому має місце вираз

,

(3.8)

з урахуванням якого формула (3.2) набуває остаточного вигляду

(3.9)

і називається формулою Бура.

Таким чином, абсолютна похідна від векторної функції за скалярним аргументом дорівнює сумі відносної похідної тієї ж функції та векторного добутку вектора на .

Формула Бура може застосовуватись до будь-якої неперервної векторної функції довільного скалярного аргументу і широко застосовується в розділі кінематики.

Наведемо деякі частинні випадки формули Бура.

1) Припустимо, що система координат є нерухомою відносно , або рухається поступально.

В цьому випадку, оскільки орти є сталими, за формулами (3.6) маємо , , і тоді формула Бура набуває вигляду .

2) Припустимо, що вектор не змінюється в рухомій системі координат , тоді і отримуємо .

3) Припустимо, що вектор не змінюється в нерухомій системі координат , тобто . Тоді маємо .

Визначимо швидкість і прискорення точки відносно нерухомої с. к. за допомогою формули Бура, для чого доведемо дві теореми.