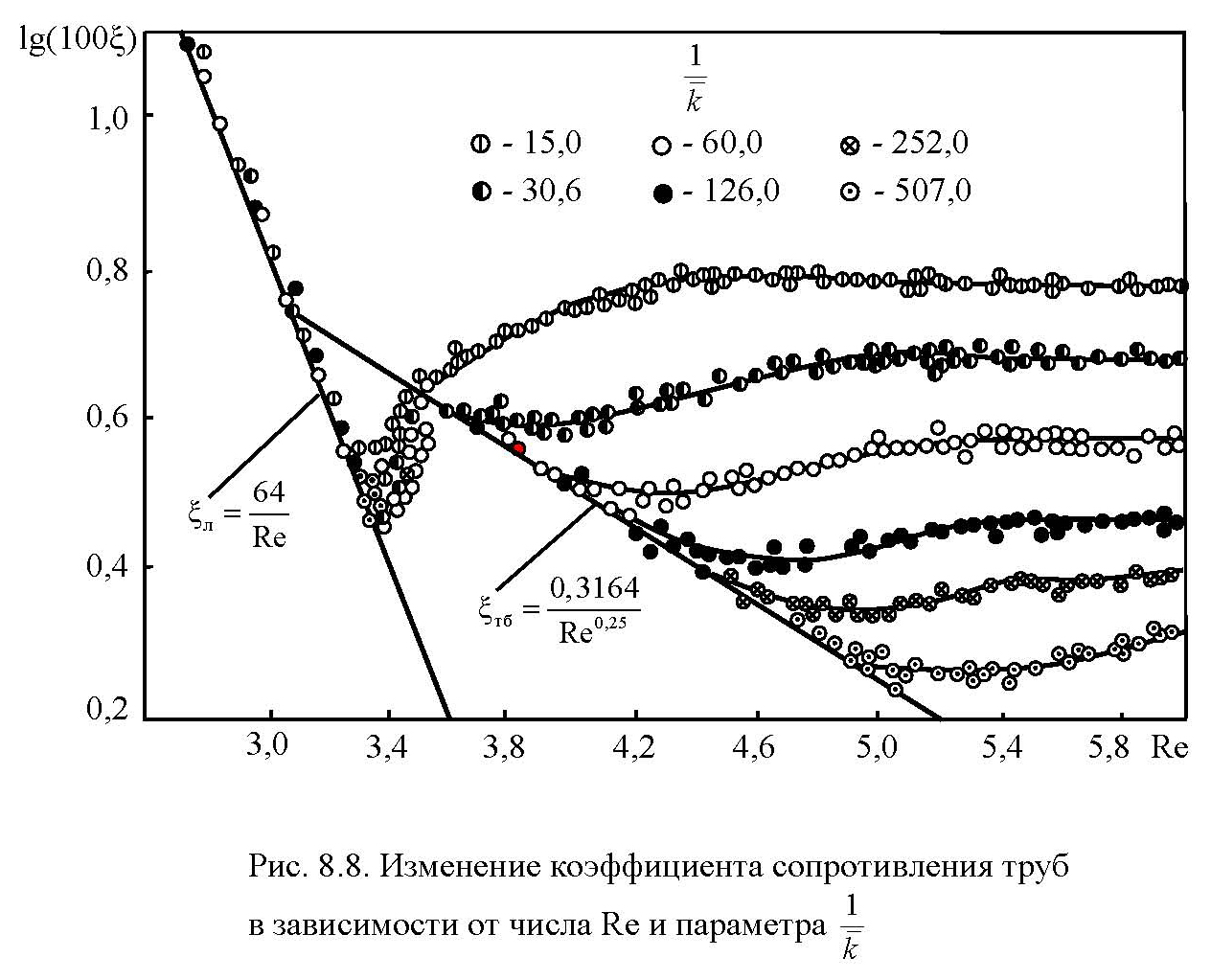
8.7. Турбулентное движение в шероховатых трубах

Шероховатость (roughness) это высота бугорка (выступа, элементов шероховатости) на поверхности твердого тела.

Режим течения, при котором труба считается гидродинамически гладкой и (Rе), наблюдается при

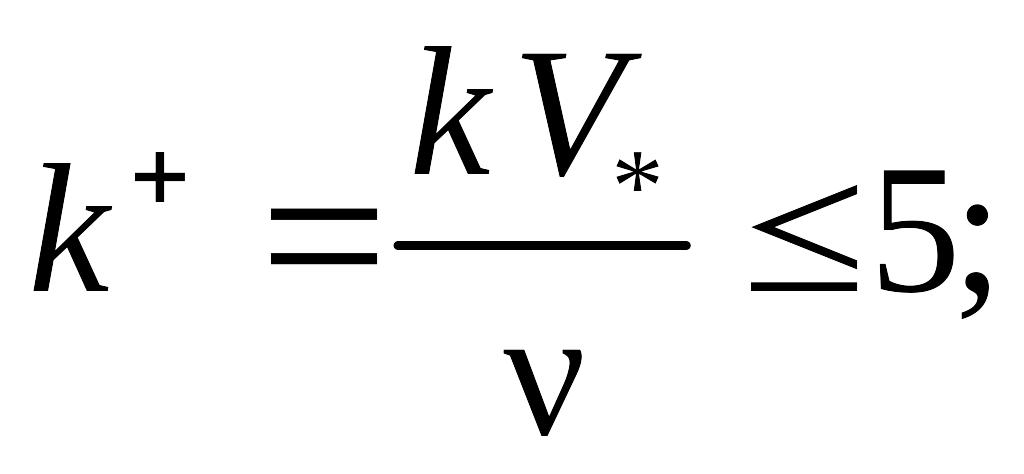
режим развитой шероховатости с квадратичной зависимостью сопротивления от скорости, когда , существует при

промежуточный режим, при котором ξ = ξ (Re; k⁺), имеет место при

5 ≤ k⁺ < 60…70.

При турбулентном течении в трубе с шероховатой поверхностью, когда неровности частично выступают за пределы ламинарного подслоя и находятся в пределах буферного (5 < k⁺ < 60),

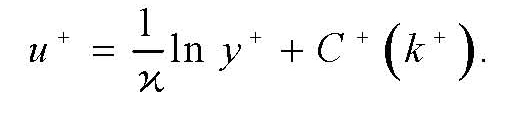
(8.157)

Коэффициент сопротивления зависит от числа Рейнольдса и относительной шероховатости k⁺ и может быть определен по формулам:

Колебрук–Уайта

(8.158)

Дополнительное сопротивление по сравнению с гладкой трубой обусловлено элементами шероховатости, выступающими в буферный слой.

При турбулентном течении с полным проявлением шероховатости поверхности трубы (2400 < Re; k⁺ > 60)

Профиль скорости определяется формулой

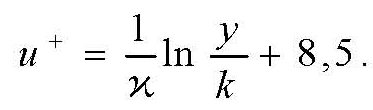
(8.160)

При Re > 10⁵ может быть использован закон дефекта скорости

(8.161)

при y⁺ > 60 y⁺ > k⁺

(8.162)

(8.163)

Коэффициент сопротивления может быть определен по формуле Кармана

(8.164)

8.8. Влияние массовых сил на движение жидкости в трубах

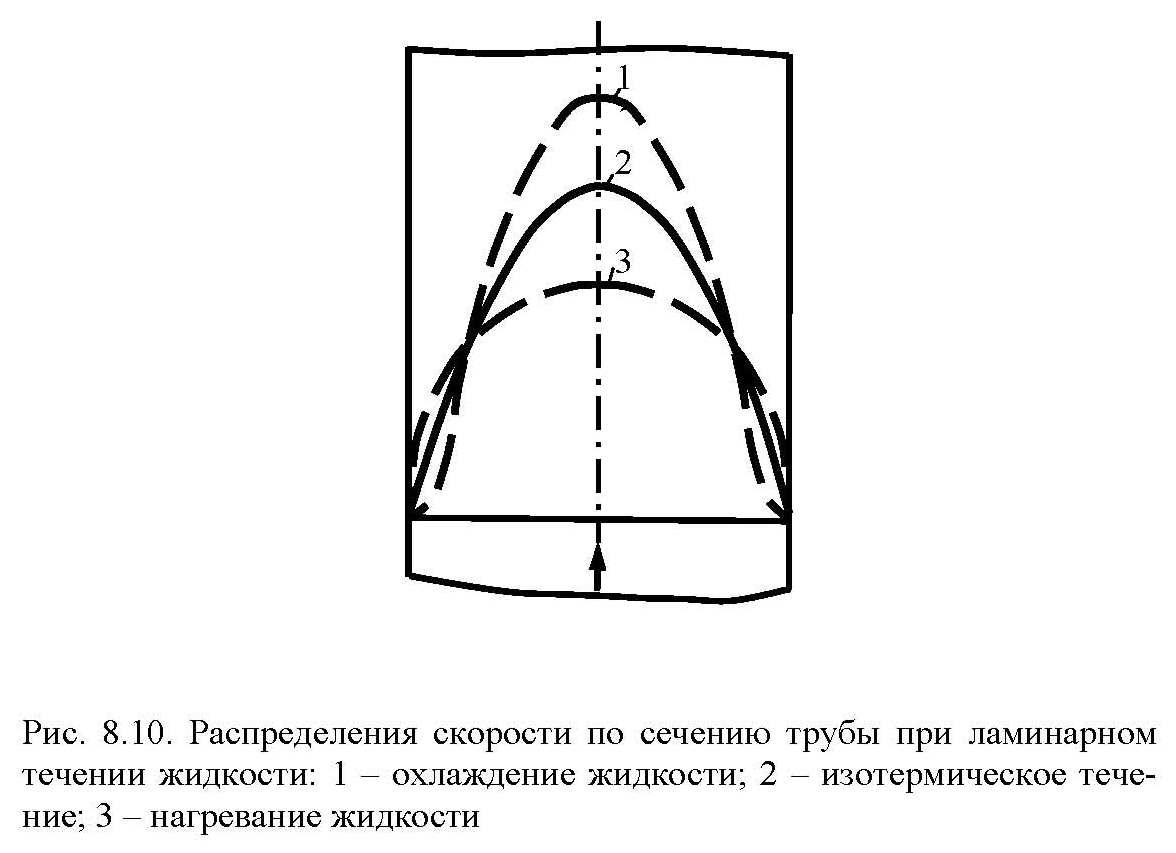
Вязкостно-гравитационное движение (combined laminar free-and-force convection) – движение жидкости, возникающее в результате наложения гравитационного свободного движения на вынужденное ламинарное движение при несущественном влиянии сил инерции. В вязкостно-гравитационном режиме течения силы вязкости и подъемные силы соизмеримы.

Параболический профиль скорости при вязкостном режиме существует только при изотермических условиях.

При вязкостно-гравитационном режиме результирующее распределение скорости в значительной степени зависит также и от взаимного направления вынужденного и свободного движений.

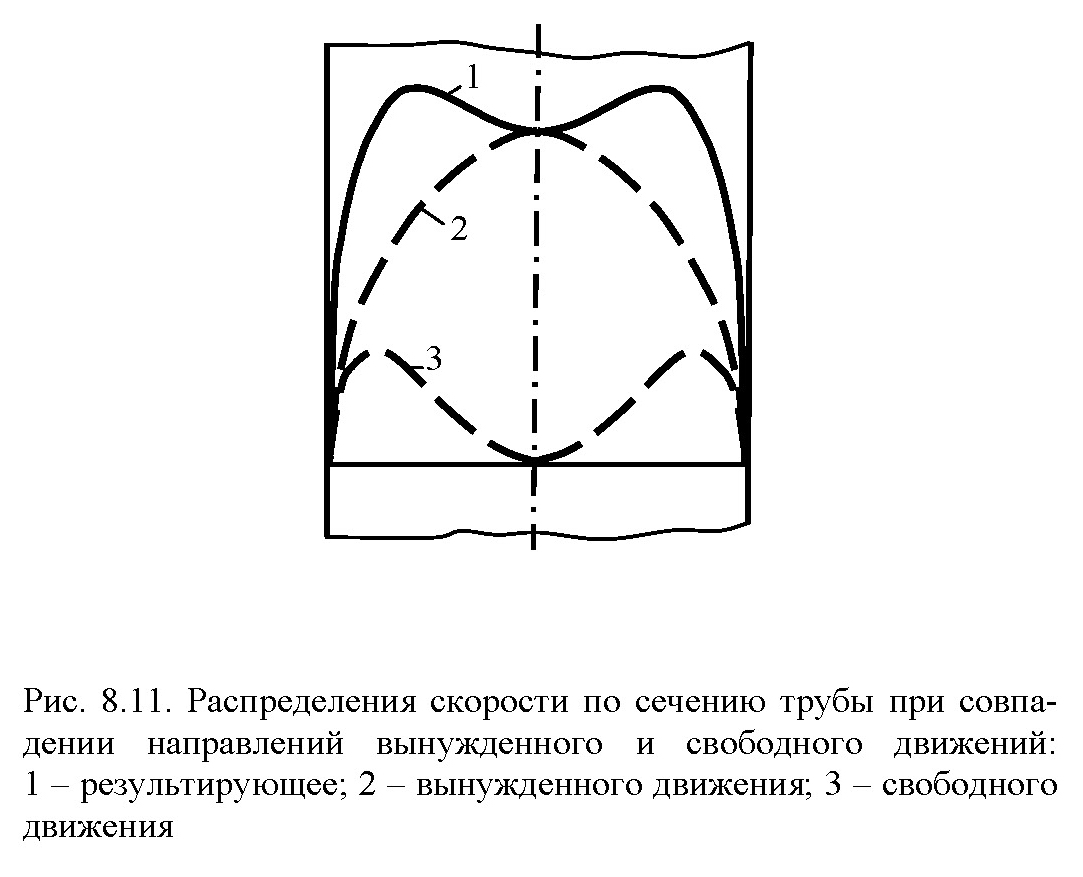
Движение жидкости, возникающее в результате наложения гравитационного свободного движения на вынужденное турбулентное, называют вязкостно-инерционно-гравитационным.

Уравнения Навье–Стокса для стационарного свободного гравитационного движения несжимаемой жидкости (6.29) в безразмерном виде запишутся следующим образом:

(8.165)

(8.166)

где – орт ускорения силы тяжести.

Из уравнения (8.165) видно, что характер течения жидкости в системе и ее сопротивление при свободно-гравитационном движении будут определяться критериями и

Центростремительные силы могут иметь внутренний или внешний характер по отношению к движущейся в трубе жидкости. В первом случае они являются следствием особой организации движения самого потока, например его закручивания, во втором – следствием движения трубы, например вращения трубы параллельно или перпендикулярно ее оси.

Система уравнений, описывающих стационарное течение вязкой несжимаемой жидкости, находящейся под воздействием одновременно гравитационных и центростремительных массовых сил в системе координат, вращающейся с постоянной угловой скоростью (такая система координат часто используется для анализа и решения задач течения жидкости во вращающихся трубах), имеет вид

(8.167)

. (8.168)

Плотность среды в общем случае , где ρ₀ – значение плотности при характерной температуре. Уравнения записаны для случая постоянных физических свойств, за исключением изменения плотности, учитываемого в члене массовых сил.

На поверхности трубы . В частном случае покоящейся трубы

Уравнения движения в неподвижной системе координат могут быть получены из уравнений (8.167), (8.168), если положить в них

Представим уравнения (8.167), (8.168) в безразмерном виде. Используем в качестве масштабных характерные величины системы: l₀ – линейный размер; V₀ – скорость; ω₀ – угловую скорость.

Тогда (8.169)

(8.170)

– число Грасгофа; – орт угловой скорости вращения; – орт ускорения силы тяжести; – центростремительное ускорение.

Для течения жидкости в трубах характерный линейный размер l₀ – диаметр трубы d = 2r₀, характерная скорость V₀ – средняя скорость течения жидкости в трубе u_ср, характерная угловая скорость – угловая скорость вращения трубы ω₀.

Безразмерный комплекс Ro – число Росби (Rossby number):

. (8.171)

По физическому смыслу число Росби, являющееся числом подобия, можно определить как отношение конвективного ускорения к ускорению Кориолиса^**, которое равно . Считается, что влияние сил Кориолиса на вынужденное течение жидкости во вращающихся каналах будет существенным при его сравнительно малой интенсивности и значении числа Росби Ro ≤ 1.

Член в правой части уравнения (8.169) характеризует вклад центростремительного ускорения.

При величине центростремительного ускорения, намного превышающей значение ускорения силы тяжести, уравнение (8.169) целесообразно записать в виде

(8.172)

где Gr_ω – «вращательное» число Грасгофа,

(8.173)

Fr_ω – «вращательное» число Фруда,

. (8.174)

Из уравнений (8.169), (8.173) видно, что характер течения жидкости во вращающейся системе в общем случае определяется критериями Fr, Re, Gr, Ro или Fr_ω, Re, Gr_ω , Ro.

В целом ряде элементов оборудования течение жидкости происходит под влиянием центростремительных сил. Повороты – одни из наиболее распространенных из них. Наибольшее распространение имеют повороты на углы φ_п, равные 45, 90 и 180º.

Поворот на 180º и схема течения в нем показаны на рис. 8.14.

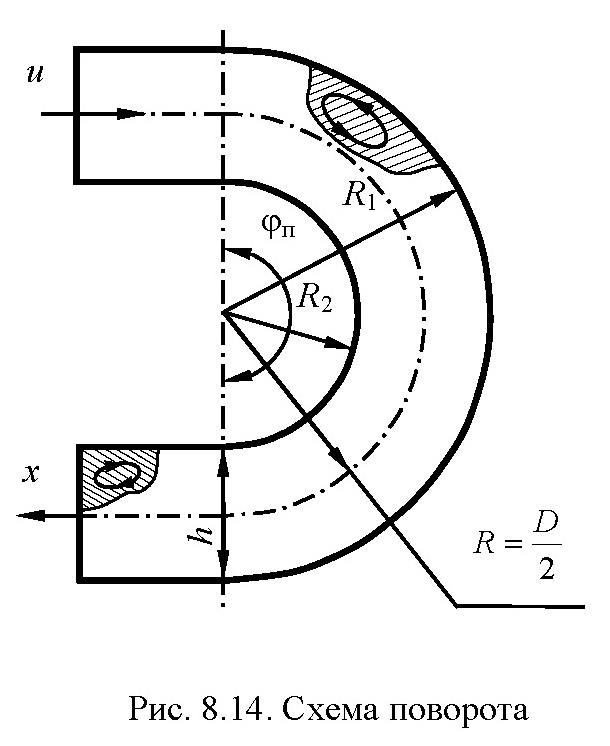
Условие радиального равновесия каждого из единичных по объему элементов потока определяется уравнением

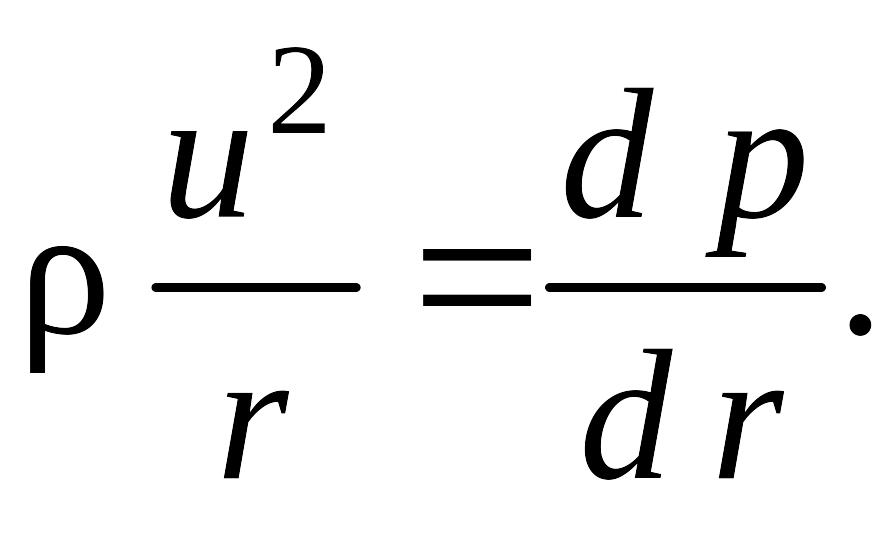(8.175)

С другой стороны, если продифференцировать уравнение Бернулли

(8.176)

Приравнивая полученные выражения, находим дифференциальное уравнение, определяющее закон изменения скорости элементов потока в направлении, перпендикулярном линиям тока (траекториям) – по радиусу,

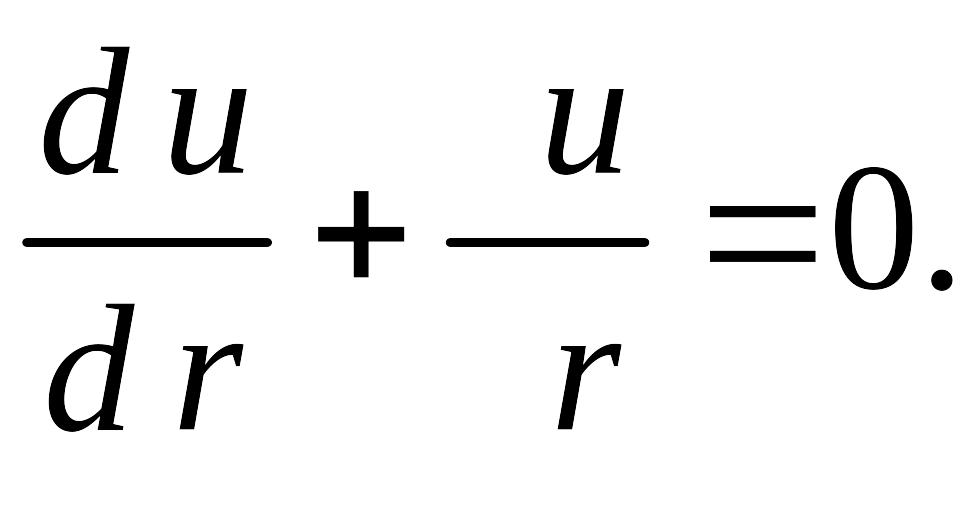(8.177)

Разделяя переменные в уравнении (8.177) и затем интегрируя его, находим

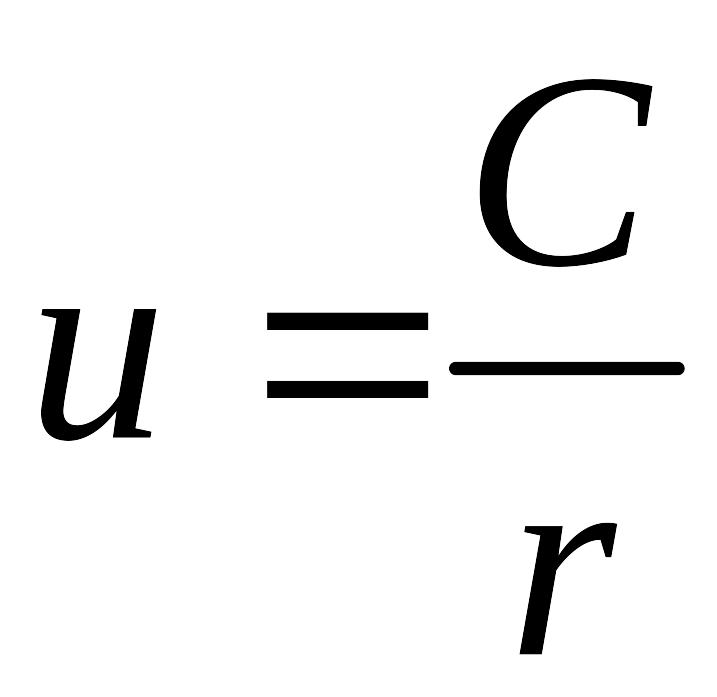, (8.178)

где C – постоянная интегрирования.

При движении жидкости по повороту скорость ее частиц убывает с ростом радиуса по гиперболическому закону.

Для определения распределения давления в повороте используем еще раз уравнение Бернулли.

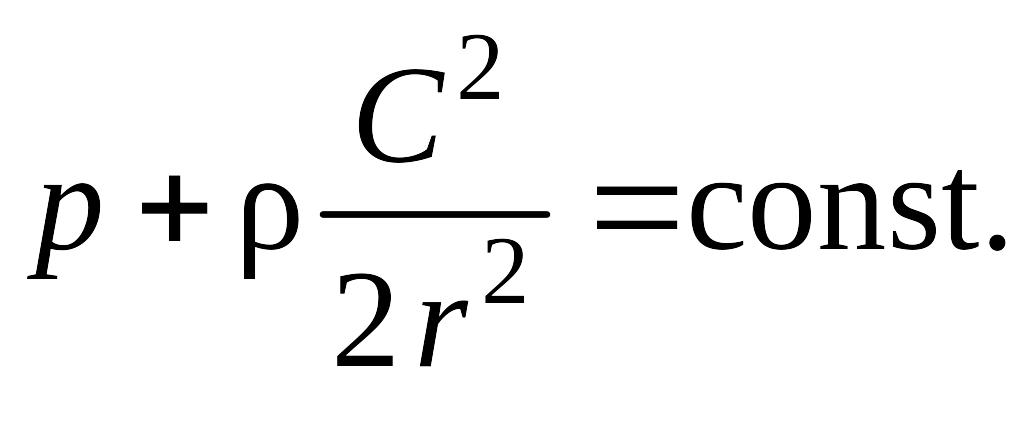(8.179)

Из уравнения (8.179) видно, что давление максимально на внешней стенке поворота и минимально на внутренней.

На рис. 8.15 показаны вторичные течения, образующиеся в повороте вследствие разности давлений, существующей на внешней и внутренней его поверхностях, и изотахи (линии одинаковых значений) безразмерных локальных скоростей.

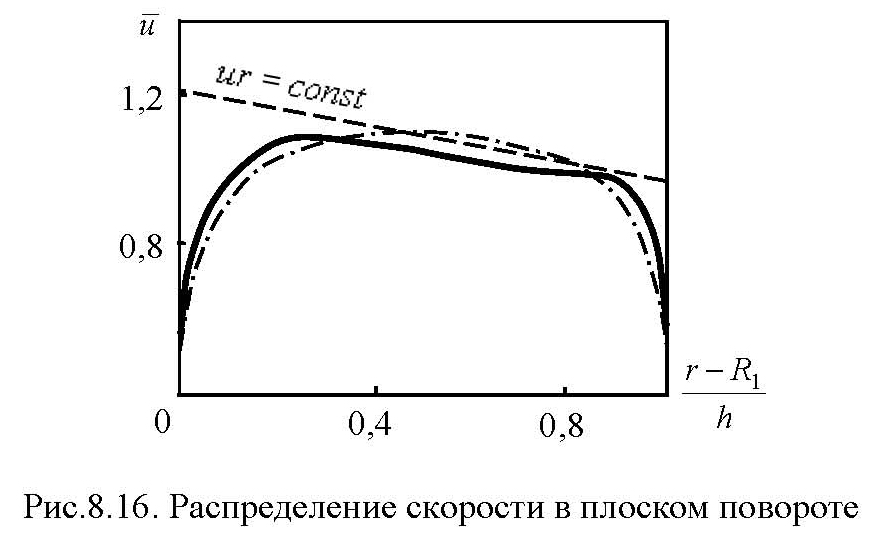
При турбулентном режиме у вогнутой стенки центростремительные силы играют активную роль, они интенсифицируют процесс турбулентного переноса. У выпуклой стенки центростремительные силы играют стабилизирующую роль.

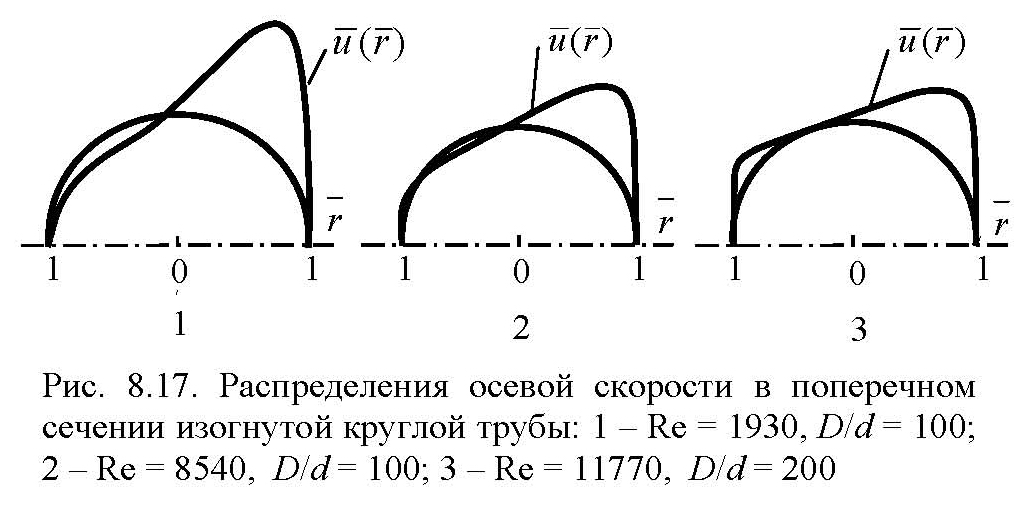
Аналитически и экспериментально установлено, что у вогнутой поверхности после потери устойчивости в ламинарном пристенном слое появляются вихри, которые имеют чередующиеся левое и правое вращения. Их оси совпадают с направлением основного потока. Вихри носят название вихрей Тейлора (Teylor)^*–Гёртлера (Gortler H.).

Таблица 8.2

Корректирующий множитель c_φ

φ	20º	40º	60º	80º	100º	120º	140º	160º	180º
	0,29	0,56	0,77	0,93	1,06	1,16	1,25	1,32	1,38

Змеевики рис. 8.18 находят применение в теплообменных аппаратах. Они выполняются из круглых труб. В отличие от поворотов, в которых действие центростремительных сил на поток носит местный характер, в змеевиках их влияние можно считать стабилизированным.

При ламинарном режиме движения вторичные течения в змеевиках начинают наблюдаться при числах Рейнольдса

(8.183)

Турбулентный режим наступает при критических числах Рейнольдса, которые можно определить по формуле

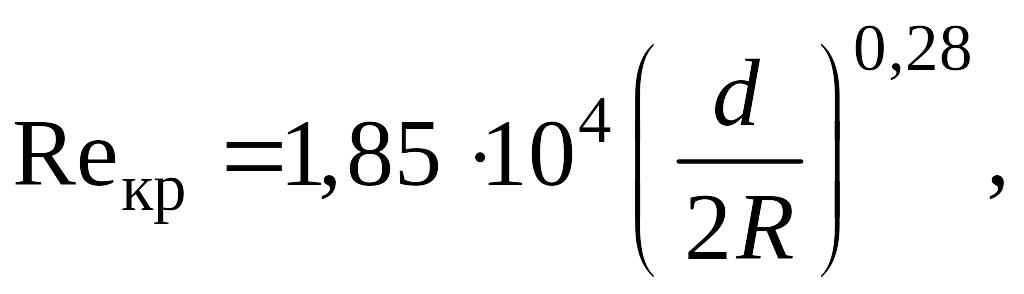(8.184)

которая справедлива при D / d = 6…400;

При D / d > 860 критический режим наступает примерно при таких же условиях, как и в прямой трубе.

В змеевиковых трубах при ламинарном течении коэффициент сопротивления трения определяется числом Дина (Dean number)

(8.186)

При Dе > 300

(8.187)

где ξ_л = 64 / Re – коэффициент сопротивления трения трубы с прямой осью при ламинарном режиме.

При 80 < De < 2000

(8.188)

При турбулентном течении

(8.189)

где ξ _тб – коэффициент сопротивления трения трубы с прямой осью при турбулентном режиме;

(8.190)

(8.191)

В области эффекты кривизны не проявляются. Закрутка потока в трубах осуществляется подводом жидкости или газа по касательной (тангенциально) к внутренней поверхности трубы или пропуском ее через специальные закручивающие устройства (винтовые вставки, лопаточные завихрители и т.п.).

Исследования сотрудников кафедры теплотехники АГТУ А.Н. Орехова и Э.Н. Сабурова показали, что коэффициент сопротивления недиафрагмированных труб с закрученным потоком может быть определен по формуле

(8.192)

где – скорость потока во входных каналах; Δ p_п – разность полных давлений потока во входных каналах и в расчетном сечении за выходным отверстием; ε_k – поправка на влияние относительной шероховатости трубы ,

(8.193)

Коэффициент сопротивления диафрагмированных труб в том же диапазоне l / d , , чисел Рейнольдса и значений параметра может быть определен по формуле

(8.194)

Коэффициент сопротивления трубы, определенный по средней скорости потока,

(8.195)

Гидравлическое сопротивление вращающейся трубы при ламинарном режиме может быть определено формулой

(8.196)

где Re_ω – «вращательное» число Рейнольдса, рассчитанное по окружной скорости вращения внутренней поверхности трубы,

(8.197)

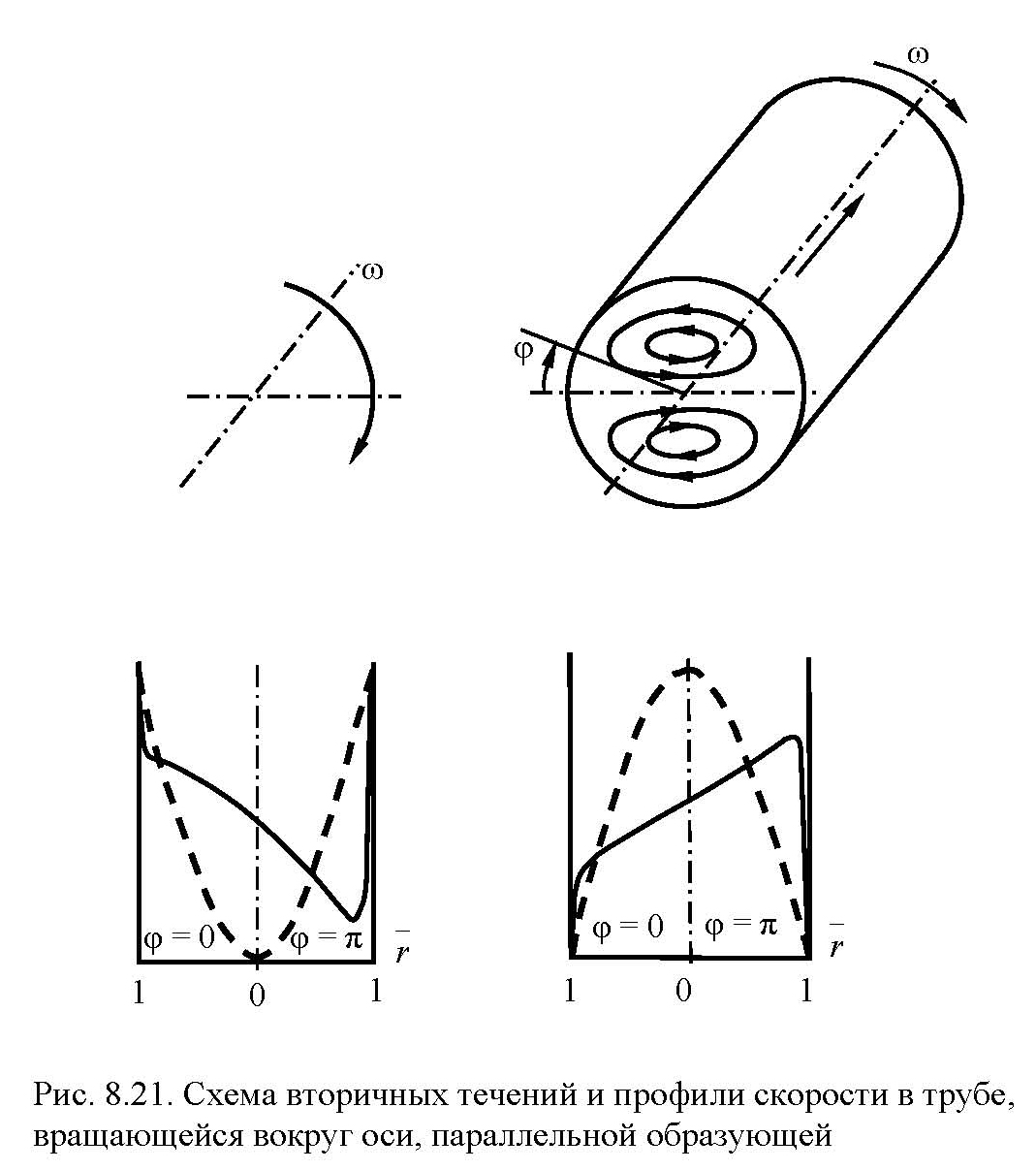
Во вращающейся трубе центростремительное ускорение оказывает стабилизирующее влияние на изотермический поток, препятствует возникновению и развитию турбулентных пульсаций скорости. При этом критическое число Рейнольдса с ростом угловой скорости вращения трубы или «вращательного» числа Рейнольдса Re_ω увеличивается:

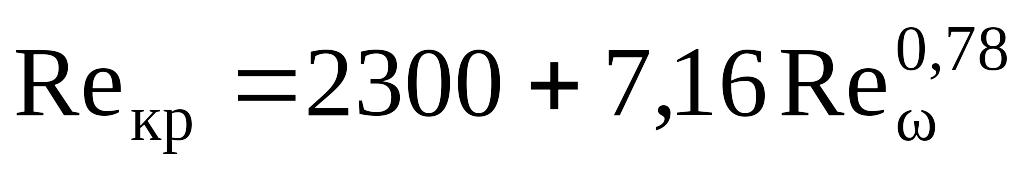. (8.198)

При турбулентном изотермическом течении при числах Росби, определенных по средней осевой скорости Ro = u_ср / (d ω), меньших единицы, с ростом ω сопротивление трубы заметно уменьшается. При Ro > 3 изменение сопротивления практически несущественно. Поэтому при этих условиях коэффициент сопротивления трения можно рассчитывать по формуле Блазиуса для неподвижной трубы с прямой осью.

Изменение плотности среды (при нагревании или охлаждении стенки) оказывает существенное влияние на течение. Это влияние вероятно можно учитывать с помощью «вращательного» числа Грасгофа Gr_ω.

Для расчета среднего по длине вращающейся трубы коэффициента сопротивления в случае ламинарного течения может быть использована формула

(8.199)

где ξ _л – коэффициент сопротивления трения в неподвижной трубе при ламинарном течении; μ_с, μ_ж – динамические коэффициенты вязкости, определяемые по температуре стенки трубы и среднемас- совой температуре жидкости соответственно; Ra_ω – «вращательное» число Релея^ (Rayleigh number),

; (8.200)

Pr – число Прандтля (Prandtl number),

При турбулентном течении жидкости сопротивление трения в трубах, вращающихся вокруг оси, параллельной образующей, можно рассчитывать по рекомендациям для неподвижных горизонтальных труб при существенном влиянии термогравитации.

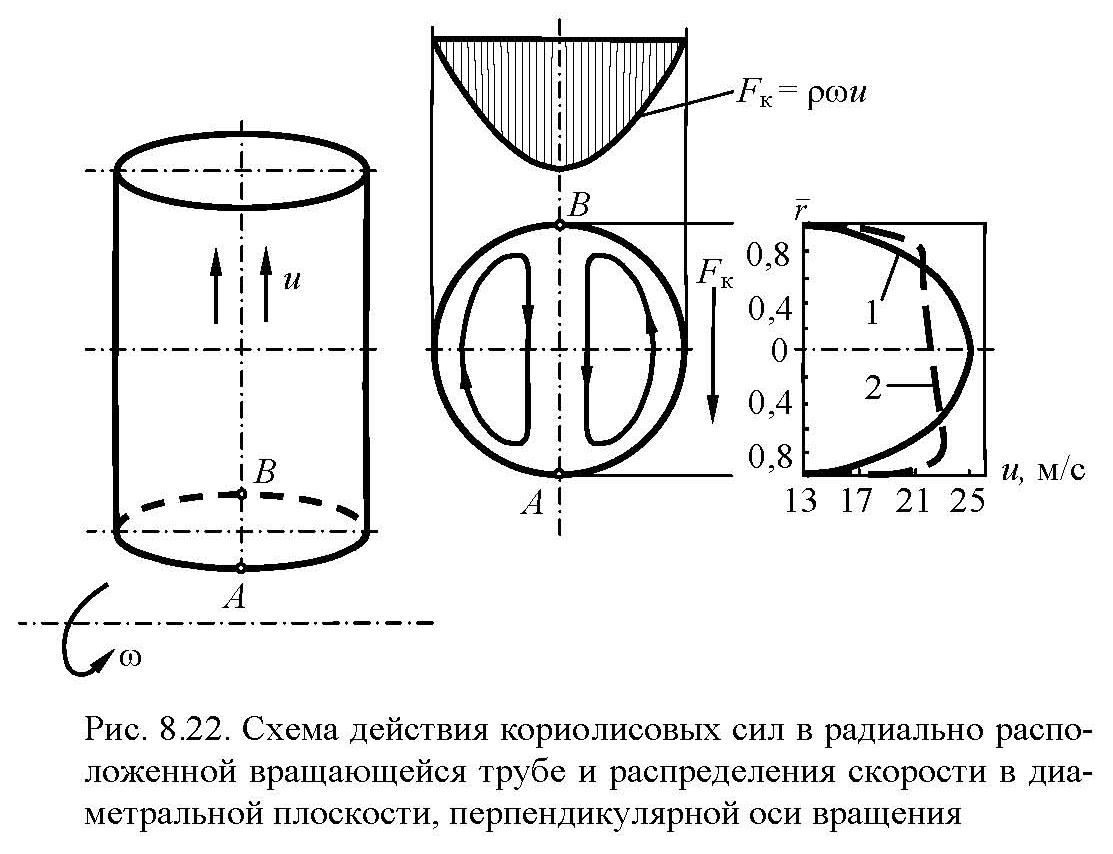
В радиально расположенных вращающихся трубах течение жидкости может происходить или в направлении роста (рис. 8.22), или в направлении уменьшения центростремительного ускорения. В этом случае поток находится под влиянием силы Кориолиса, которая существенно изменяется в поперечном сечении трубы.

Сопротивление трубы как при ламинарном, так и турбулентном режимах течения при направлении потока жидкости от оси вращения повышается с увеличением скорости вращения трубы.

При изотермическом ламинарном течении коэффициент сопротивления трения

(8.202)

где ξ _л – коэффициент сопротивления трения неподвижной трубы при ламинарном течении.

Из опытов установлено, что преобладающее влияние центростремительных сил по сравнению с силами Кориолиса, наступает при

(8.203)

где l_ср– половина длины трубы.

Для изотермического турбулентного течения коэффициент сопротивления трения

(8.204)

где – коэффициент сопротивления трения неподвижной трубы при турбулентном течении;

(8.205)

*^* Кориолис (Coriolis) Гюстав Гаспар (1792–1843) – французский ученый в области механики. Труды по теории относительного движения, ввел понятия силы и ускорения Кориолиса.

* Тейлор (Teylor) Джефри Инграм (1886–1975) – английский ученый в области механики, иностранный член АН СССР (1966). Труды по теории турбулентности, исследования по аэро-, гидро- и газовой динамике и др.

 Релей Джон Уильям, лорд Рэлей (Lord Rayleigut), (1842–1919). Английский физик. Член (1873) и президент (1905–1908) Лондонского королевского общества, иностранный член-корреспондент Петербургской АН (1896). Лауреат Нобелевской премии (1904).