8.6. Профили скорости и законы сопротивления при турбулентном движении жидкости в круглой трубе
При турбулентном течении профиль скорости в трубе более заполнен, чем при ламинарном. Основное изменение скорости наблюдается в пристеночной области, занимающей примерно 15 % от радиуса трубы.
Полный универсальный профиль скорости может быть описан при трехслойной модели движения жидкостей в пристеночной области следующей системой уравнений:
ламинарный подслой при y+ ≤ 5
(8.81)
переходный участок при 5 ≤ y+ ≤ 30
(8.82) или 
(8.83)
турбулентная область при y+ ≥ 30
(8.84) или 
(8.85)
Рассмотренные уравнения могут использоваться для определения коэффициента ε τ.
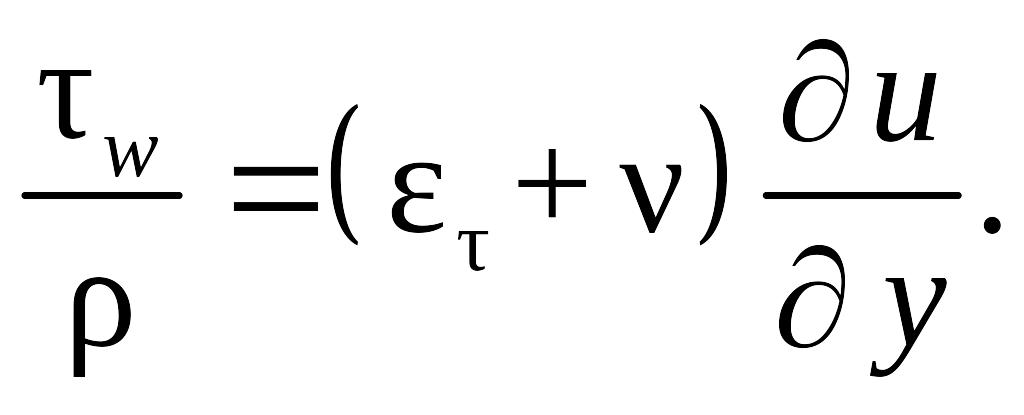(8.87)
Дайслер (Deissler) для двухслойной модели рекомендует зависимости (8.88)–(8.91).
При y+ < 26
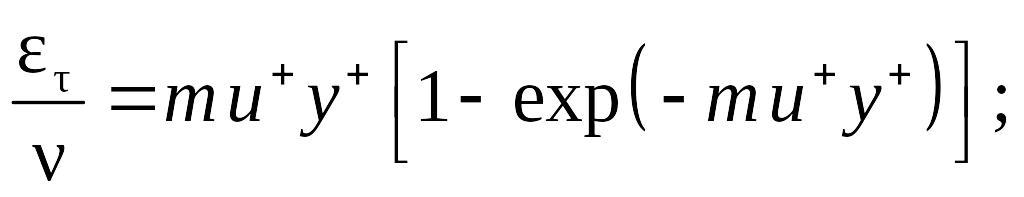(8.88)
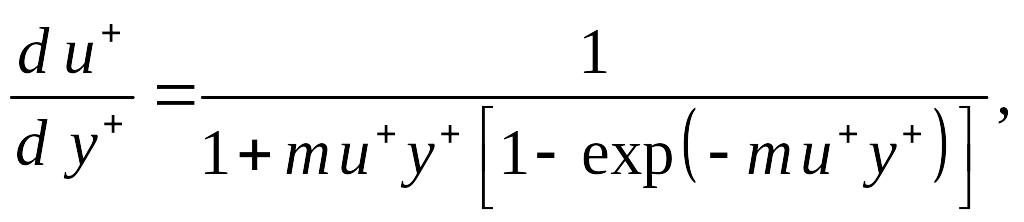(8.89)
где m = 0,0154;
при y+ > 26
(8.90)
(8.91)
где
– безразмерная граница пристеночной
области.
Формула Рейхардта (Reichardt) для профиля скорости в круглой трубе радиусом r0 имеет вид
(8.94)
Для относительного кинематического коэффициента ετ / ν им предложены следующие зависимости:
при y+ ≤ 50
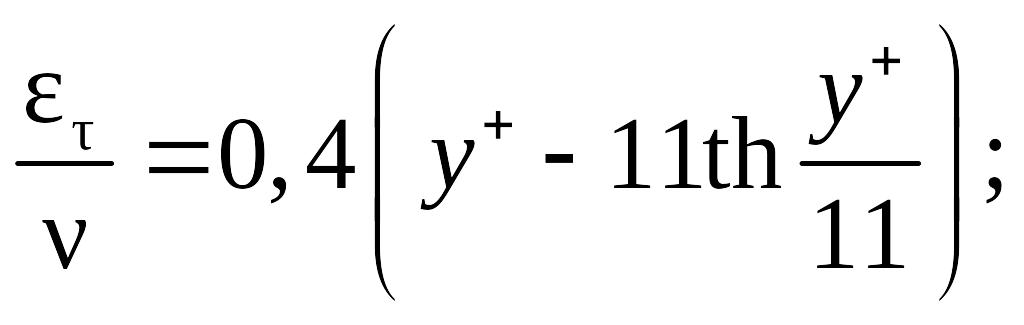(8.95)
при y+ > 50
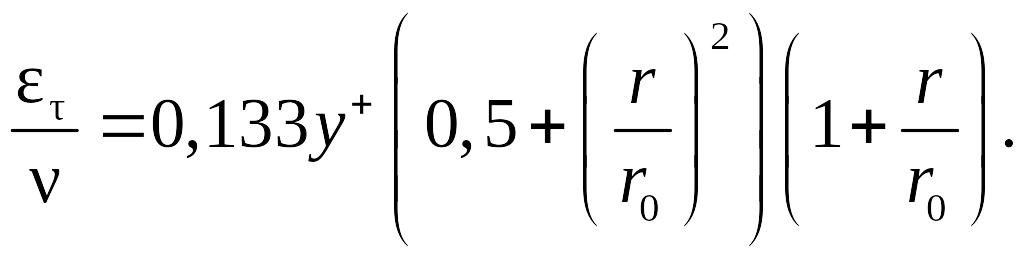(8.96)
На рис. 8.7 сопоставлены относительные коэффициенты ετ / ν по формулам Прандтля, Рейхардта и Дайслера в пристеночной зоне при Re = 105. Из рисунка видно, что в большей части потока турбулентный перенос намного интенсивней молекулярного.
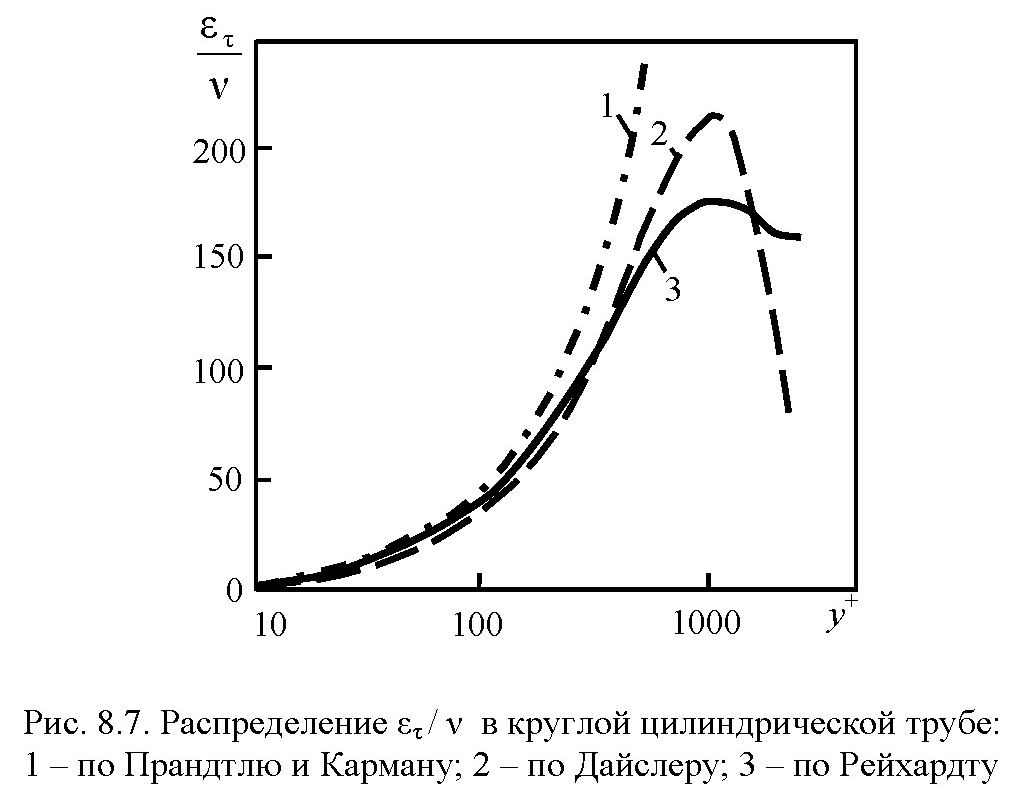
Кривые, соответствующие двухслойной схеме Прандтля и трехслойной Кармана, показывают, что эти схемы весьма приближенно аппроксимируют действительные зависимости.
при y = r0:
(8.97)
Если вычесть из выражения (8.97) значение u / V*, определенное по формуле (8.85), то получим так называемый дефект скорости
(8.98)
Используя это уравнение, определим среднюю скорость в трубе:
(8.99)
Или иначе
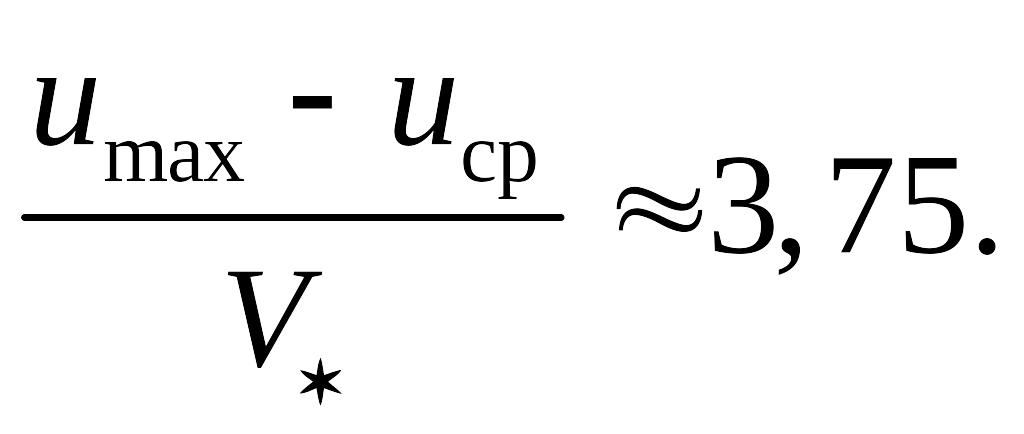(8.100)
Отношение
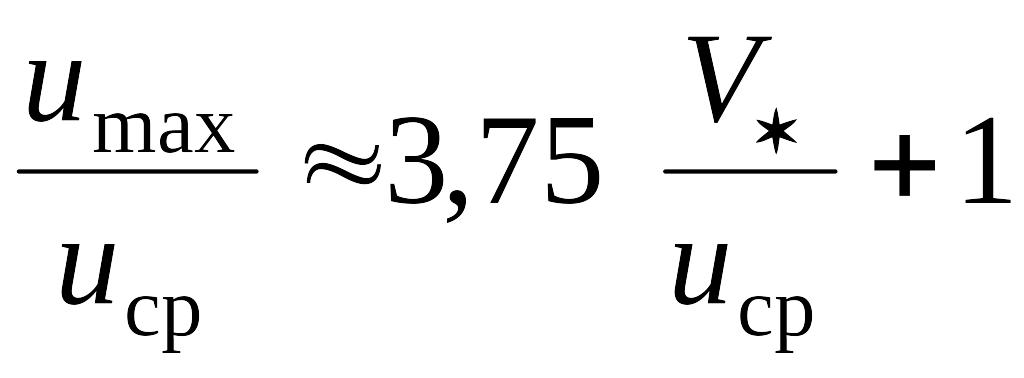(8.101)
уменьшается с ростом Re. При турбулентном движении профиль u = u (y) оказывается более заполненным, чем при ламинарном.
Универсальному логарифмическому закону распределения скорости соответствует и логарифмический закон сопротивления трения. С его выводом можно познакомиться в учебном пособии.
(8.102)
(8.103)
(8.104)
(8.105)
(8.106)
Поскольку
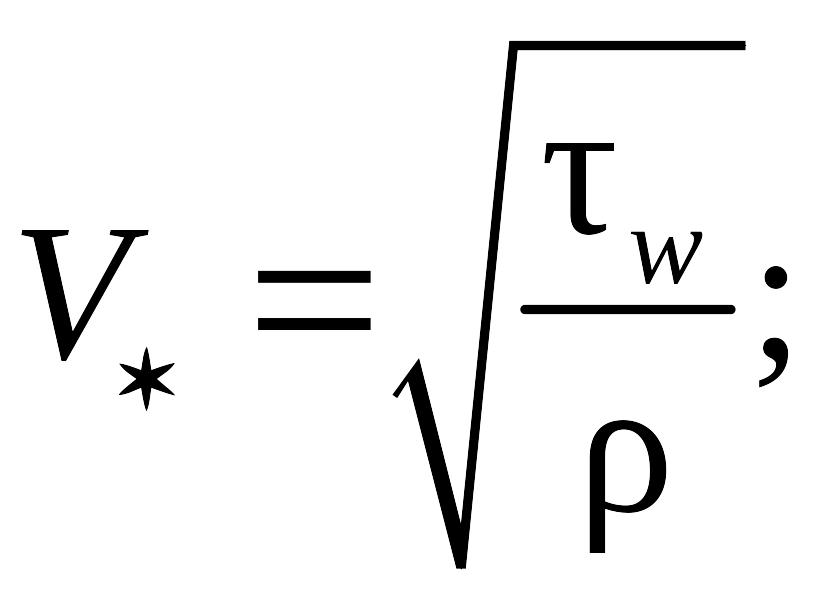(8.107)
(8.108)
(8.109)
(8.110)
Логарифмический закон сопротивления можно представить в виде
(8.111)
где С, D – постоянные.
Наилучшее приближение к опыту дает закон сопротивления, аппроксимируемый следующей формулой:
(8.112)
Более удобны эмпирические зависимости, предложенные Никурадзе
(8.113)
и Филоненко
(8.114)
Часто в расчетах наряду с логарифмическими универсальными зависимостями для скорости и сопротивления используют более простые, но не универсальные степенные эмпирические формулы.
(8.115)
(8.116)
В общем случае показатели n и m, а также коэффициент a зависят от числа Rе. Причем численные значения a и m однозначно связаны с показателем n.
Частным случаем степенного закона сопротивления трения является известная формула Блазиуса (Blasius)
(8.117)
которой соответствует степенной профиль скорости вида
(8.118)
Формула (8.117) справедлива при Reкр < Re < 5 ∙104.
Отношение uср / umax при степенном профиле (8.115) можно определить следующим образом:
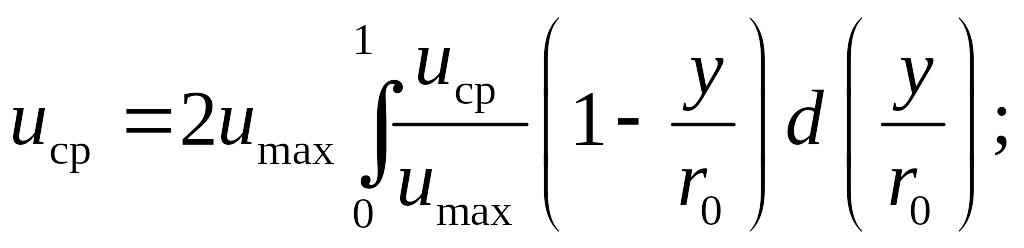
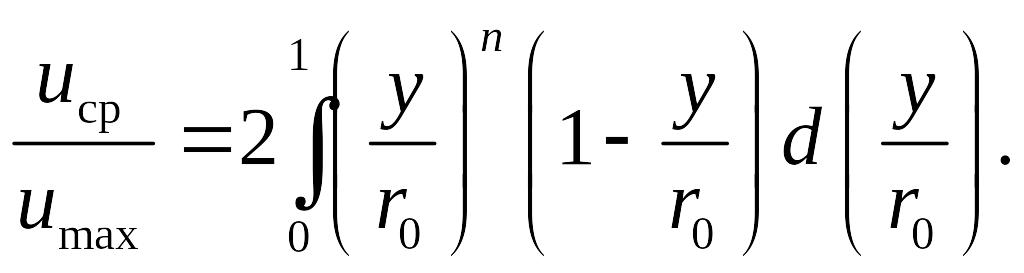
(8.119)
В табл. 8.1 приведены значения umax / uср в зависимости от n, рассчитанные по формуле (8.119).
Таблица 8.1
Значения umax / uср и C (n) при различных Rе и n
Rе |
4∙103 |
11∙105 |
4,7∙105 |
1,3∙106 |
3∙106 |
n |
|
|
|
|
|
|
1,264 |
1,224 |
1,194 |
1,173 |
1,156 |
C (n) |
7,76 |
8,74 |
9,71 |
10,6 |
11,5 |
Рассмотрим связь величин a и m с показателем n в степенной формуле распределения скоростей.
При установившемся движении в трубе
(8.120)
(8.121)
(8.122)
(8.123)
При
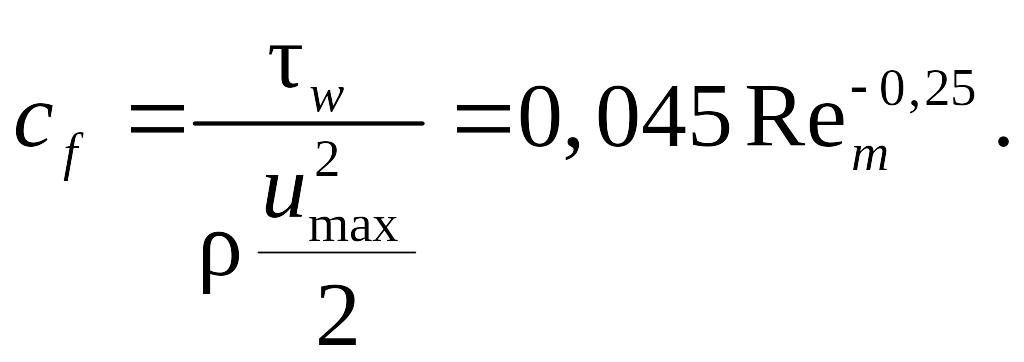(8.134)