8. ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ

ВЯЗКОЙ ЖИДКОСТИ В ТРУБАХ И ВДОЛЬ ПЛАСТИНЫ

8.1. Ламинарное и турбулентное движение.

ПЕРЕХОД ЛАМИНАРНОГО ДВИЖЕНИЯ В ТУРБУЛЕНТНОЕ

(8.1)

8.2. ЛАМИНАРНОЕ ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ

Рассмотрим стабилизированное ламинарное движение жидкости в бесконечно длинной цилиндрической круглой трубе с диаметром d = 2r₀.

Ось x направим вдоль оси трубы, а начало координат разместим вдали от входа потока в трубу – за начальным участком, в области стабилизированного течения. Массовыми силами и неизотермичностью потока пренебрегаем.

При принятых условиях υ уравнения движения могут быть записаны в виде

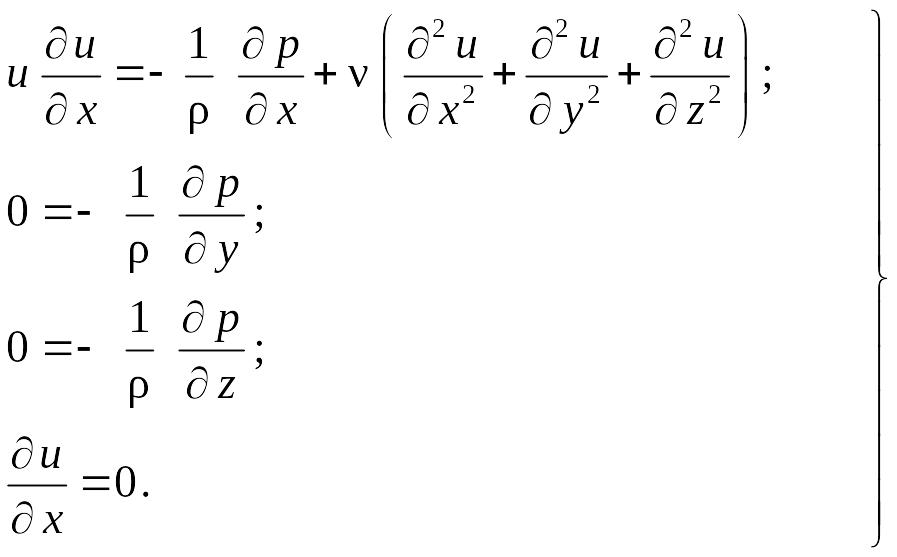(8.2)

Скорость u является функцией лишь координат y и z или радиуса, а давление p зависит только от координаты x, является постоянным в каждом сечении. В этом случае

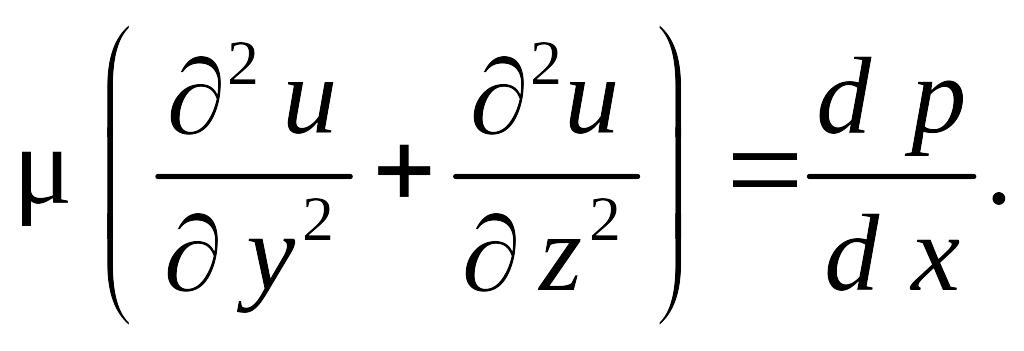(8.3)

(8.4)

Исходное уравнение сводится к линейному

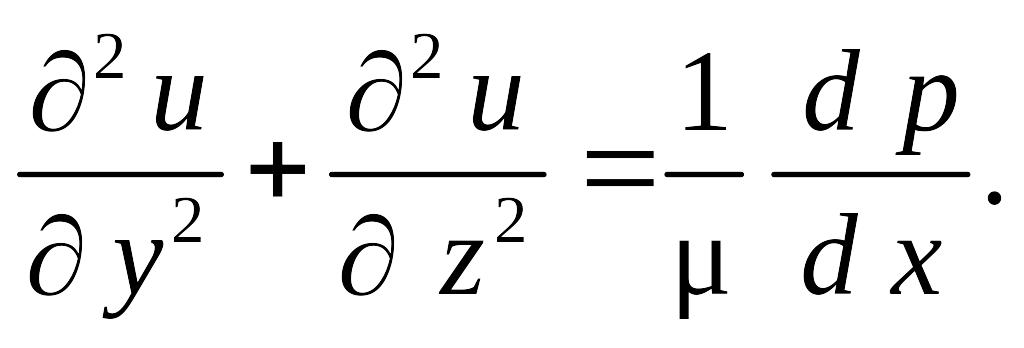(8.5)

Если перейти на цилиндрическую систему координат, в которой x = x, y = rcosφ, z = rsinφ, то

(8.6)

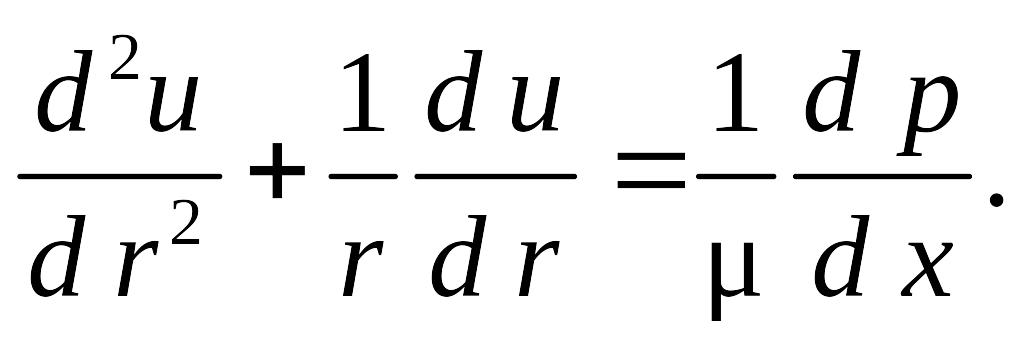(8.7)

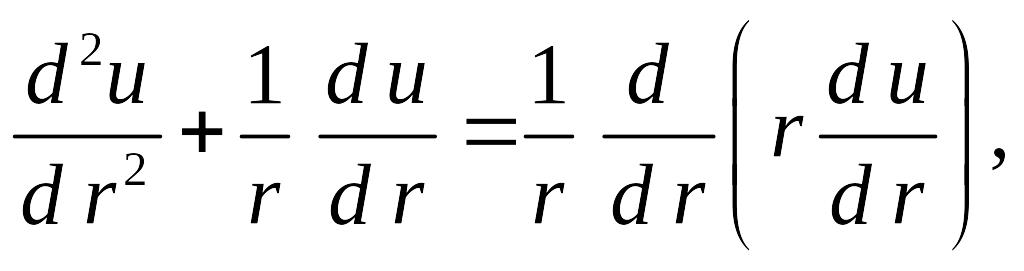
то уравнение (8.7) окончательно можно записать следующим образом:

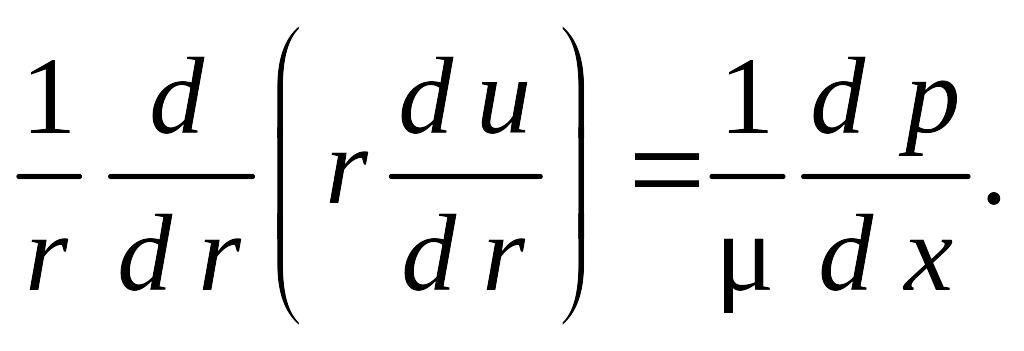(8.8)

После последовательного двойного интегрирования найдем общее решение уравнения (8.8)

(8.9)

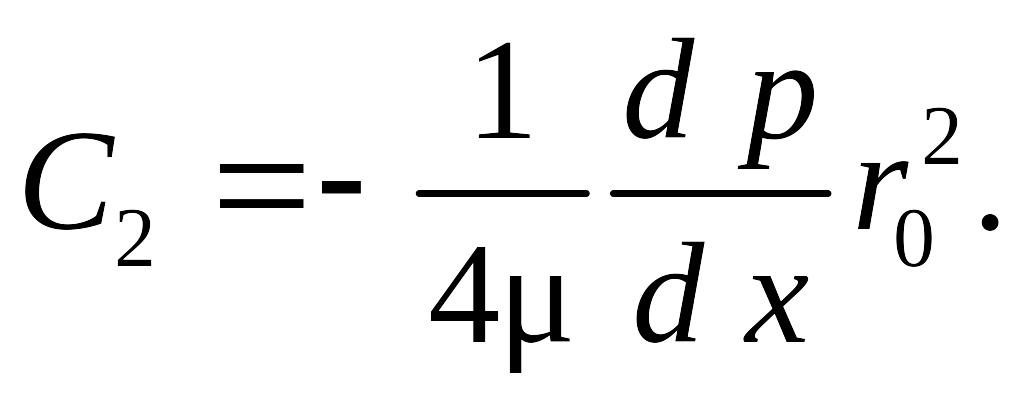
Распределение скорости в трубе параболическое:

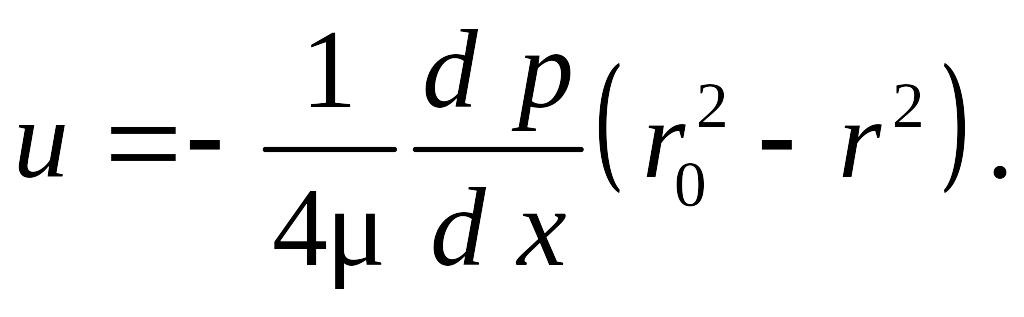(8.10)

Обозначим

(8.11)

Распределение скорости по сечению трубы:

(8.12)

Максимальная скорость в сечении

(8.13)

(8.14)

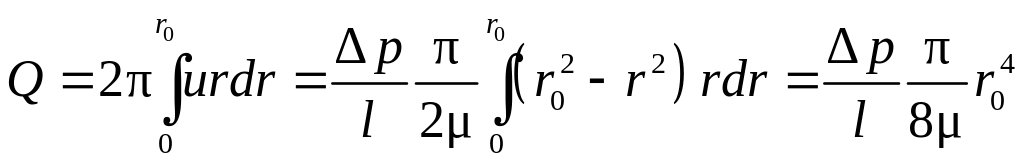. (8.15)

Средняя скорость движения потока в трубе:

(8.16)

(8.17)

(8.18)

(8.19)

(8.20)

(8.21)

Выводы:

коэффициент сопротивления трения круглой цилиндрической трубы с прямой осью при ламинарном течении обратно пропорционален числу Рейнольдса;

сопротивление трубы пропорционально первой степени скорости;

безразмерное распределение скорости ū не зависит от числа Re;

безразмерный удельный перепад давления (D/l)La = является постоянным числом.

Мощность N, необходимая для обеспечения заданного расхода жидкости Q(м³/с):

(8.22)

8.3. Основные понятия теории турбулентного движения. Уравнения рейнольдса

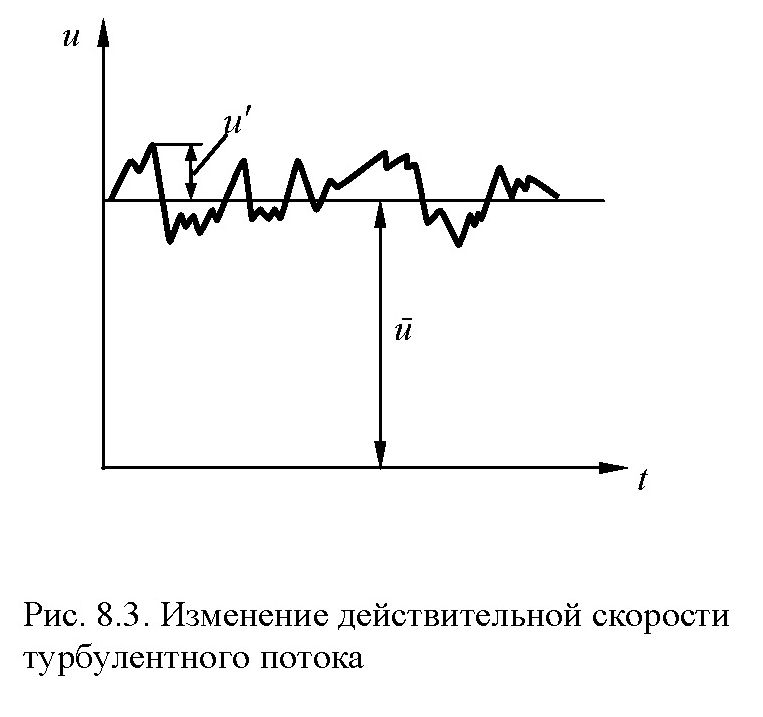
Актуальное – мгновенное значение пульсирующей скорости турбулентного потока в данной точке (instantaneons velocity) складывается из некоторого осредненного значения скорости (time mean velocity) и пульсационной составляющей (fluctuating velocity), т.е.

(8.23)

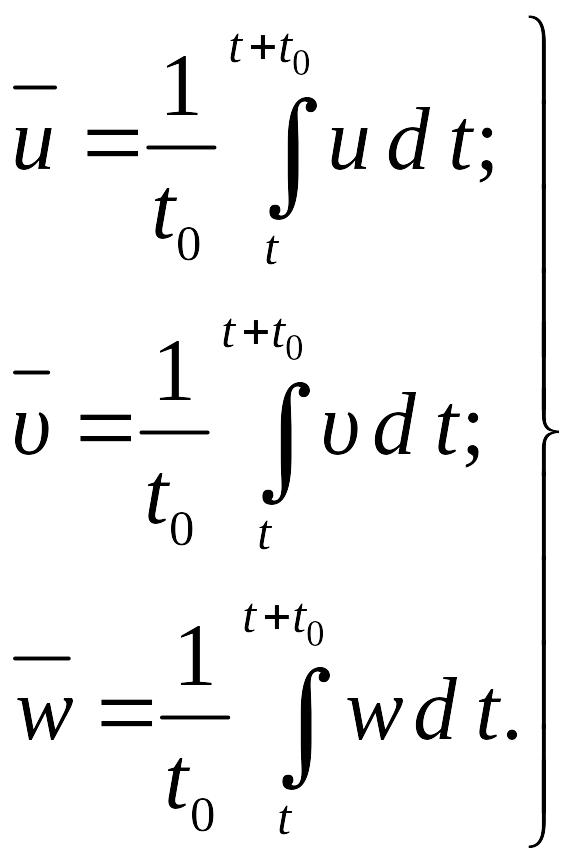(8.24)

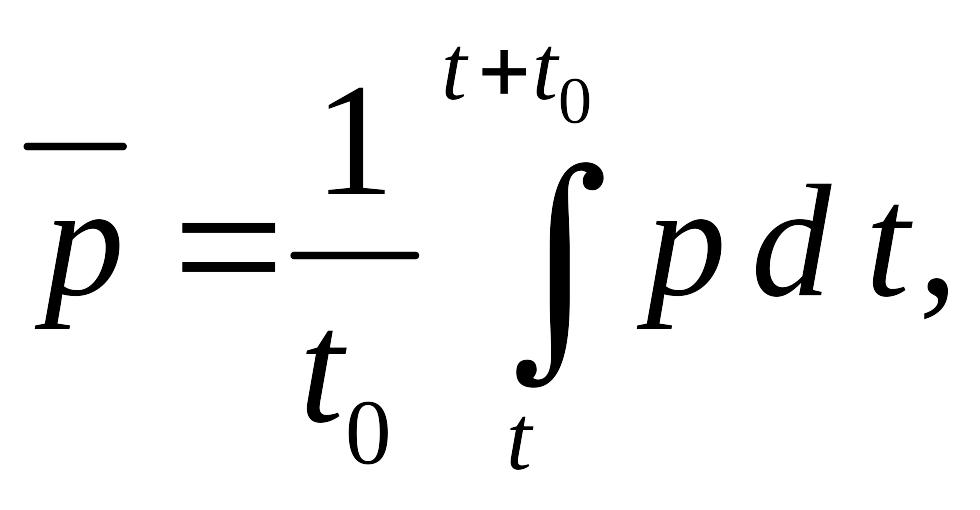(8.25)

Средняя амплитуда пульсаций:

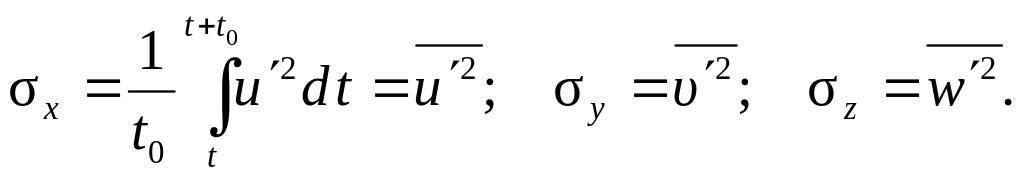(8.26)

Степень интенсивности турбулентности – отношение квадратного корня из средних квадратичных пульсаций скорости к местной или общей осредненной скорости потока:

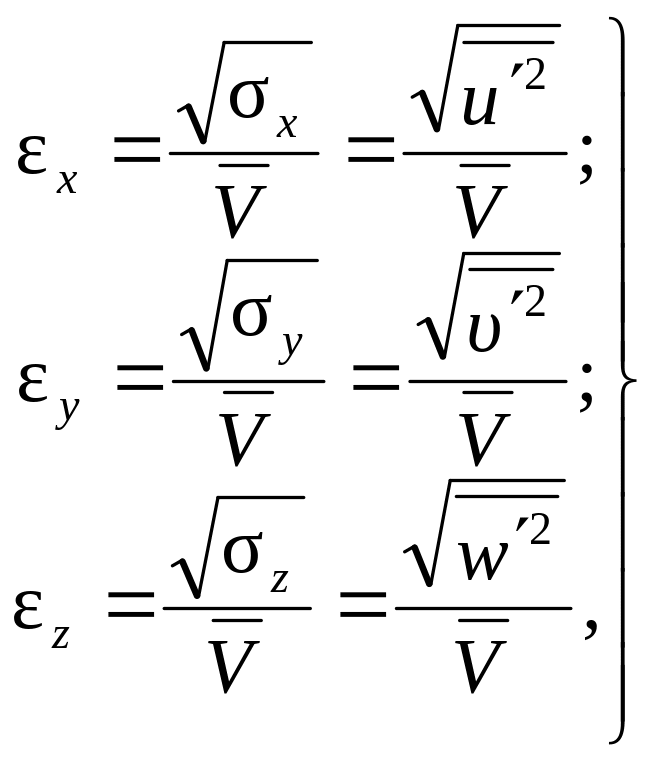(8.27)

Степень турбулентности:

(8.28)

Правила операций осреднения

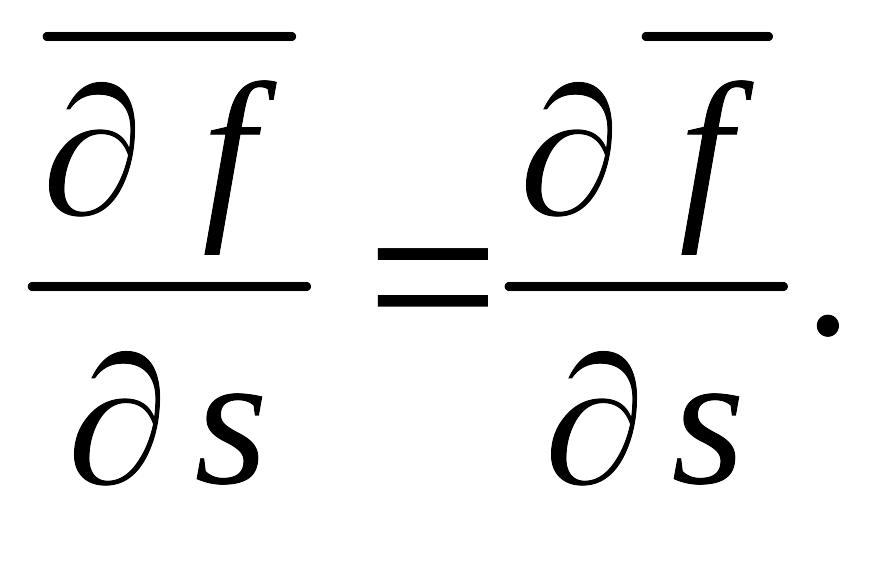
При отсутствии массовых сил уравнения движения вязкой несжимаемой жидкости имеют вид

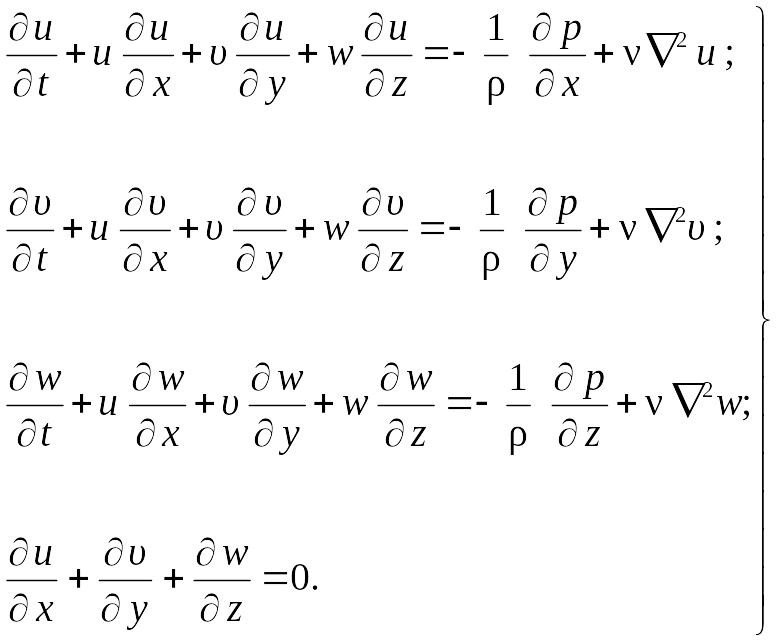(8.29)

Используя уравнение неразрывности, первое уравнение системы (8.29) можно представить следующим образом:

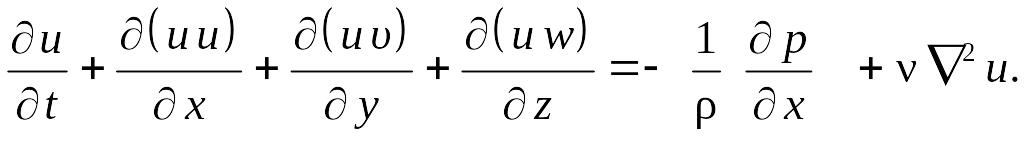(8.30)

При ρ = const, ν = const в результате его осреднения получаем

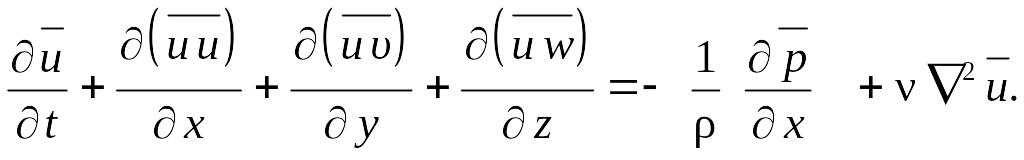(8.31)

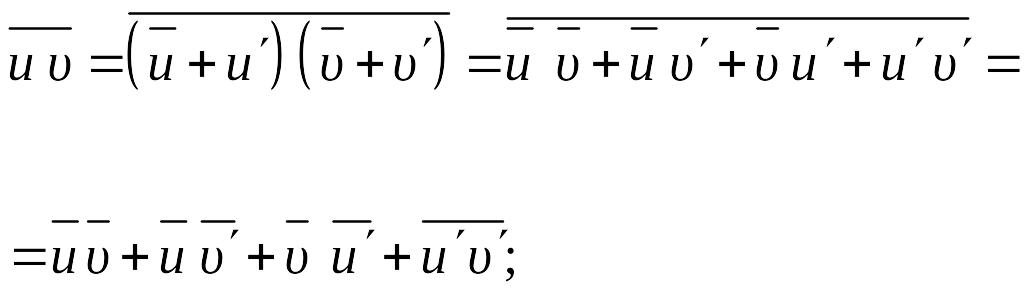
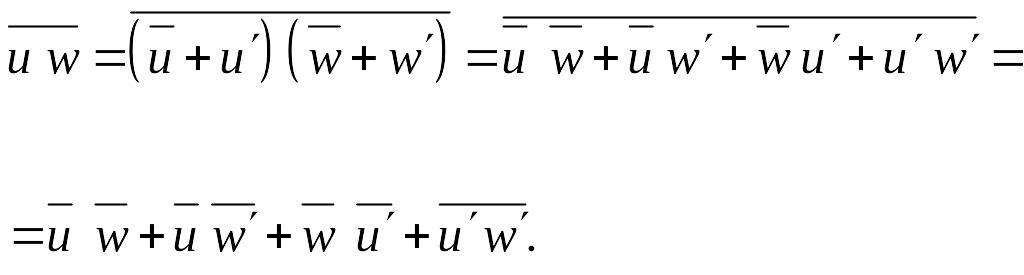
, поэтому

Используя полученные равенства, уравнение (8.31) представим в виде

(8.32)

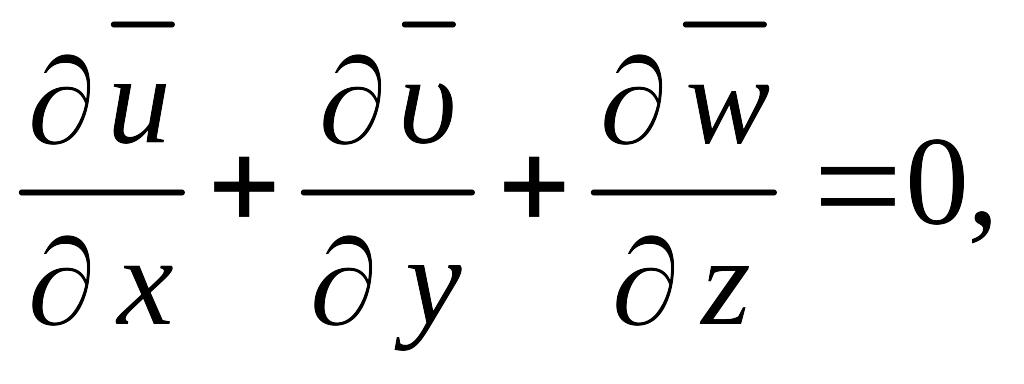(8.33)

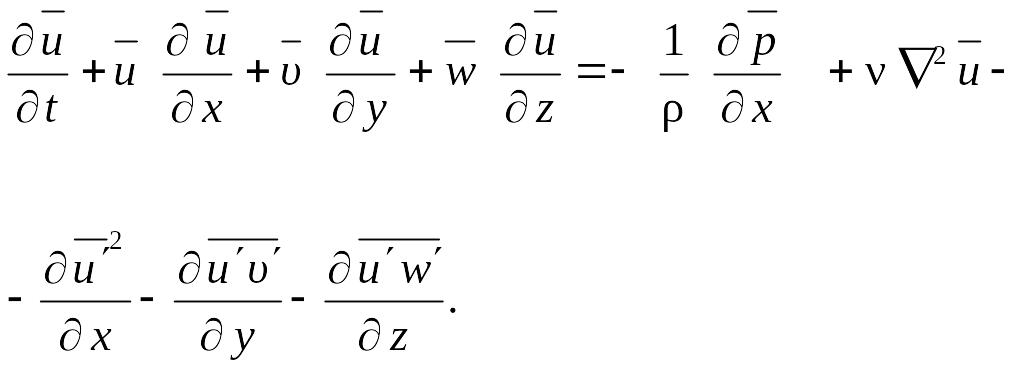(8.34)

Уравнения осредненного турбулентного движения:

Иначе полученные уравнения можно представить следующим образом:

Если уравнения Рейнольдса сравнить с уравнениями движения сплошной среды в напряжениях

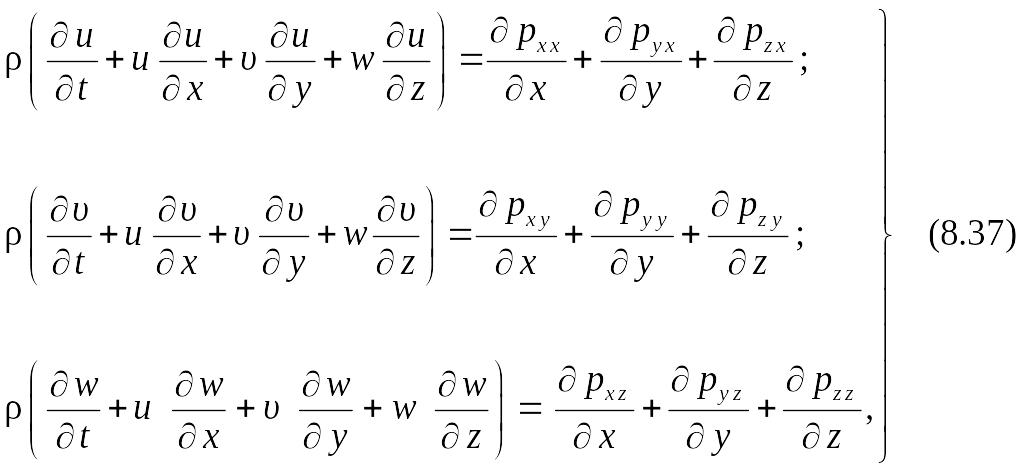
то соответствующие компоненты напряжений системы (8.36) можно представлять в виде

Новые слагаемые

– дополнительные турбулентные напряжения.

Тензор турбулентных напряжений:

. (8.40)