Однородные позиционные системы счисления

Однородные позиционные системы счисления являются частным случаем позиционных систем при pi = рj для всех i и j, т. е. в них веса отдельных разрядов представляют собой ряд членов геометрической прогрессии со знаменателем р. Поэтому число в однородных системах может быть представлено полиномом вида

или причем , а знаменатель геометрической прогрессии p носит название основания системы счисления. Очевидно, что основанием однородной позиционной системы может быть любое целое число, так как в определении позиционных систем счисления не наложено никаких ограничений на величину основания. Поэтому возможно бесчисленное множество позиционных систем счисления. Например, десятичное число A = 777 в троичной системе счисления с символами 0, 1, 2 будет иметь следующий вид:

А = 1001210₃.

Обычно число в однородной позиционной системе записывается в сокращенном виде:

а название системы определяет ее основание! десятичная, двоичная, восьмеричная и т. д.

Для любой позиционной системы счисления справедливо, что ее основание изображается символами 10 в своей системе, т. е. любое число в своей системе p можно записать символами этой системы в виде

Правильная дробь в р-ичной системе счисления будет иметь вид

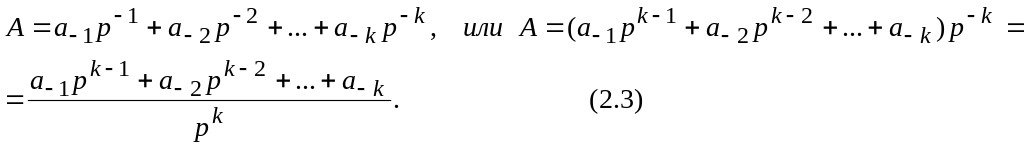
Таблица 2.2

Основные системы
16	10	8	3	2		16	10	8	4	3	2
0	0	0	000	0000		9	9	11	21	100	1001
1	1	1	001	0001		A	10	12	22	101	1010
2	2	2	002	0010		B	11	13	23	102	1011
3	3	3	010	0011		C	12	14	30	110	1100
4	4	4	011	0100		D	13	15	31	111	1101
5	5	5	012	0101		E	14	16	32	112	1110
6	6	6	020	0110		F	15	17	33	120	1111
7	7	7	021	0111		10	16	20	40	121	10000
8	8	10	022	1000

Этим выражением пользуются при чтении десятичных дробей. Этим же приемом целесообразно пользоваться при чтении дробей с любым другим основанием р.

Некоторые числа, представленные в однородных системах с различными основаниями, приведены в табл. 2.2.

Из таблицы видно, что вес i-гo разряда Ri числа в позиционной системе счисления представляет собой отношение . Если разряд имеет вес Ri = 10^m, то следующий старший разряд имеет вес: Ri+1 =10^m+1, а младший — Ri-1 = 10^m-1. Такая взаимосвязь разрядов требует передачи информации между ними (переносов при сложении и заемов при вычитании).