6.4. Умножение чисел в д-кодах

Умножение чисел в Д-кодах сводится к последовательному сумми­рованию частных произведении, получаемых при умножении множи­мого на очередную цифру множителя. При этом умножение сопровож­дается расшифровкой значения очередной i-й тетрады множителя, которая представляется в виде (_____i и сдвигом множителя на четыре разряда сразу.

Самым простым приемом расшифровки тетрады является последо­вательное вычитание единицы из значения тетрады до получения нуля и соответственно прибавление множимого в сумматор на каждом так­те. Так как при умножении множимого на тетраду возможно пере­полнение разрядной сетки сумматора (вследствие того что множимое прибавляется к сумме частичных произведений столько раз, сколько единиц содержится в данном десятичном разряде множителя), то в нем необходимо предусмотреть дополнительную тетраду для учета возникающих переносов. Из четырех возможных способов умноже­ния в двоично-десятичной системе целесообразно применять только один: умножение младшими разрядами множителя со сдвигом сум­мы частичных произведений вправо. Умножение обычно производится в прямом коде, т. е. знак результата определяется суммой знаков сомножителей по модулю 2.

Пример. Умножить в прямом Д2 коде числа

А = -0,45; [А]_пр= 1,0111 1000;

В =+0,24; [В]_пр = 0,0101 0111.

Знак результата определяется так же, как и в случае двоичной системы: 1  1, Для выполнения операции умножения необходим трех тетрадный сумматор.

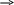Рг В СМ

0101 _ 0111 0011 0011 0011

0001 +A + 0111 1000

_ 0110 1010 1011

0001 Поправка + 1101 1101

_ 0101 +А 0111 1000

0001 + 0111 1000

_ 0100 1111 0000

0001 Поправка + 1101 0011

0011 1100 0011

+ А + 0111 1000

Конец анализа 0100 0011 1011

Поправка + 0011 1101

0100 0110 1000

+ А + 0111 1000

0100 1110 0000

Поправка + 1101 0011

0011 0101 Сдвиг на 4 разряда 0100 1011 0011

- 0001 0011 0100 1011 0011

0100 +A + 0111 1000

1100 0011

- 0001 Поправка + 1101 + 0011

0011 Конец анализа 1001 0110

+A + 0111 1000

0100 0000 1110

Поправка + 0011 + 1101

0100 0011 1011 0011

Таким образом, [А • В]_пр= 1,0100 0011 1011 0011.

Если сомножители имеют по п десятичные разрядов, то в регистре множимого должно быть п

разрядов (тетрад) справа от запятой, а в сумматоре должно быть п основных разрядов, одна тетрада переполнений и один (п+1)-й дополнительный десятичный разряд (ДДР), который предназначен для округления результата (в коде Д2 для округления достаточно иметь один дополнительный двоичный разряд). При необходимости сохранить все 2п разрядов произведения справа от сумматора должен быть еще сдвиговый регистр для младших разрядов произведения. Регистр множителя должен иметь п тетрад справа от запятой. Причем, если младшая тетрада этого регистра выполнена в виде реверсивного счетчика, т. е. счетчика, который может прибавлять или вычитать единицу, то операцию умножение можно ускорить в среднем почти в два раза. В этом случае необходимо иметь специальный разряд для записи 1, если при суммировании в счетчике-тетраде появится код 10₁₀.

Такой состав оборудования объясняется следующим образом. Если очередная цифра множителя, находящаяся в младшей тетраде (счетчике) регистра множителя, равна или меньше 5₁₀, то производится многократное прибавление множимого к сумме частых произ­ведений сумматора. При каждом суммировании множимого вычи­тается 1 из счетчика. Такие действия выполняются до тех пор, пока на счетчике не появится код 0. Если же очередная цифра множителя равна или больше 6₁₀ то производится многократное вычитание (сло­жение в дополнительном Д-коде) множимого из суммы частичных произведений сумматора. При каждом вычитании множимого к содер­жимому счетчика прибавляется 1. Вычитания продолжаются до тех пор, пока в счетчике не появится код 10₁₀. При этом в специальный разряд записывается 1.

По окончании анализа текущей тетрады множителя производится сдвиг на одну тетраду вправо суммы частичных произведений и множителя. При этом в счетчик регистра множителя сдвигается следующая тетрада множителя, к которой прибавляется содержимое специ­ального разряда, т. е. 1, если она была там записана. Операция умно­жения заканчивается сдвигом множителя и суммы частичных произве­дений. Всего должно быть выполнено п сдвигов. На последнем сдвиге в счетчик сдвигается нуль множителя. Если при этом в него добав­ляется 1 из специального разряда, то операция умножения заканчи­вается прибавлением множимого к сумме частичных произведений. В результате получается

2п-разрядное произведение.

Таким образом, описанный алгоритм позволяет существенно со­кратить время умножения практически без изменения состава обору­дования. Если необходим п -разрядный результат, то произведение округляется путем прибавления к ДДР, т. е. к (п + 1)-й тетраде, числа 5₁₀.

Пример. Задано А=0,367₁₀, В=0,583_10. Найти произведение С=АВ и округлить до 3-х разрядов. Все действия для простоты выполняем в десятичном коде. Квадратной рамкой обведён счётчик в регистре множителя (PrB), счетчик тактов (разрядов) умножения (СЧТ) и специальный разряд (СПР). На сумматоре (СМ) самый левый разряд (от запятой) – двоичный (знаковый), а второй слева (разряд переполнений)- десятичный.

СМ РГ В СПР СЧТ

00,000000 ,58 3 0 0

+ 00,367 [+a₁₀]д -1

00,367000 ,58 2

+ 00,367 [+a₁₀]д -1

00,734000 ,58 1

+ 00,367000 [+a₁₀]д -1

01,101000 ,58 0

00,110100 Сдвиг ,05 8 +1 1

+ 19,633 [-a₁₀]д +1

1 9,743100 ,05 9

+ 19,633 [-a₁₀]д +1

1 9,376100 ,05 10 1

Сдвиг ,00 5 +1 +1 2

1 9,937610 ,00 6 0

+ 19,633 [-a₁₀]д +1

19,570610 ,00 7

+ 19,633 [-a₁₀]д +1

1 9,203610 ,00 8

+ 19,633 [-a₁₀]д +1

1 8,836610 ,00 9

+ 19,633 [-a₁₀]д +1

1 8,469610 ,00 10 1

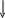
Сдвиг ,00 0 +1 +1 3

1 9,846961 ,00 1 0

00,367 [+a₁₀]д -1

0 0,213961 ,00 0

+ 5 окр

00,214

Таким образом, C=AB = 0,214₁₀

Дальнейшим развитием описанного способа ускорения операции умножения в Д- кодах является формирование кратных множимого А. Например, при наличии кратных 2А и 4А частое произведение

Таблица 6.2

Текущая цифра множителя	Вид операции	Текущая цифра множителя	Вид операции
0 1 2 3 4	0 +А +2А +А+2А +4А	5 6 7 8 9	+А+4А -А -А-4А -2А -А

формируется следующим образом в зависимости от текущей циф­ры множителя В (табл. 6.2).

При этом, если предыдущая цифра В была больше пяти, то действие на очередном шаге надо увеличить на + 1А. Как видно из таблицы, в худшем случае для данного способа потребуется всего 2 действия алгебраического сложения при получении одного частного произве­дения, а в среднем для этого необходимо I, 2 сложений — вычитаний. Способ позволяет анализировать очередную цифру множителя про­стыми аппаратными средствами. Для его реализации потребуется еще два регистра для хранения 2А и 4А или коммутатор для формирова­ния 4А и 2А путем сдвига А соответственно на 2 и 1 разряд.

Другой прием, применяемый для ускоренного умножения, сво­дится к следующим пошаговым преобразованиям произведения:

АВ = 2А В/2, если В — четное число;

АВ = 2А (В-1)/2 + А, если В — нечетное число.

Пример. Задано А = 35, В = 34. Найти С = А • В.

35 • 34=2 • 35•34/2 = 70 • 17 = 140 • 8+70 = 280 • 4 + 70 = 560 • 2 + 70= 1120 • 1 + 70= 1190.

Таким образом, С= АВ= 1190.

При этом удвоение числа означает его сдвиг влево, а деление на 2 — сдвиг вправо. Так как двоичные сдвиги производятся над двоич­ными кодами, то требуется коррекция тетрад на каждом шаге. Как видим, сложения производятся только при нечетном множителе. Наибольшее их количество возможно при В = 2_n— 1 и равно (п— 1), а при В = 2ⁿ производятся только сдвиги множимого и множителя.

Качественную оценку эффективности рассмотренных способов ум­ножения дает сравнение числа сложений, которое необходимо для получения полного произведения по каждому из способов, напри­мер, при В = 0,583:

1. Только суммирование множимого. Количество сложений: 5 + 8 + 3 = 16.

2 . Суммирование и вычитание множимого, которое при этом практически имеет вид В =1,4 23, где черта над цифрой означает вычитание. Тогда количество сложений составит: 1 + 4 + 2 + 3 = 10.

3 Суммирование и вычитание кратных множимого. Количество сложений: 2+1+2 = 5.

4. Пошаговое формирование произведения путем двоичного сдви­га множимого и множителя. Количество сложений: 1 + 1 + 1 + 1 == 4.

Таким образом, если учесть, что в реальных ЭВМ количество раз­рядов значительно больше трех, то выигрыш в быстродействии при выполнении умножения ускоренными методами окажется еще бо­лее существенным.