4Понятие референц-эллипсоида. Особенности меркаторской проекции, применяемой при создании мнк. Географические координаты и их разности.

Референц-эллипсоид (от лат. referens — сообщающий, вспомогательный), земной эллипсоид с определёнными размерами и положением в теле Земли, служащий вспомогательной математической поверхностью, к которой приводят результаты всех геодезических измерений на земной поверхности и на которую тем самым проектируются пункты опорной геодезической сети. К поверхности Р.-э. относят также топографические съёмки и составляемые по ним карты. Для приведения геодезических измерений к поверхности Р.-э. необходимо знать высоты земной поверхности над поверхностью Р.-э. и отклонения отвеса во всех точках, в которых эти измерения производились. Высоты земной поверхности над поверхностью Р.-э. определяются методами геометрического и астрономо-гравиметрического нивелирования, но на топографических картах высоты земной поверхности указываются относительно уровня моря.

  Размеры Р.-э. задаются размерами его большой а и малой b полуосей или размером большой полуоси и величиной полярного сжатия , определяемого равенством

  Положение Р.-э. в теле Земли определяется так называемыми исходными геодезическими датами, т. е. заданием геодезических координат проекции на Р.-э. нормалью к нему некоторой точки земной поверхности, а также геодезического азимута некоторого направления и высоты геоида над Р.-э. в той же точке.

  В геодезических и картографических работах разных стран используются различные Р.-э. В СССР и других социалистических странах в качестве Р.-э. применяется Красовского эллипсоид, который характеризуется величинами:

а = 6 378 245 м,

 = 1: 298,3.

  Положение (ориентировка) эллипсоида Красовского в теле Земли определено геодезическими координатами центра круглого зала Пулковской обсерватории:

ш ирота В = 59° 46’ 18’’, 55,

долгота L = 30° 19’ 42’’, 09,

азимут направления на пункт Бугры

А = 121° 10’ 38’’, 79.

  Высота геоида над Р.-э. в Пулкове принята равной нулю.

Равноугольная цилиндрическая проекция Меркатора

Проекция, предложенная в 1569 г. голландским картографом Герардом Кремером, носившим, кроме того, латинское имя Меркатор, получила название проекции Меркатора. Эта проекция удовлетворяет двум основным требованиям, предъявляемым к проекциям для морских навигационных карт:

- она равноугольна;

- локсодромия на проекции изображается прямой линией.

Первое свойство проекции Меркатора — равноугольность выражается равенством масштабов по всем направлениям, т. е. а = b = m = n. Вследствие этого бесконечно малый кружок на поверхности Земли на карте в проекции Меркатора изобразится также бесконечно малым кружком.

Второе свойство определило вид географических меридианов и параллелей проекции: они представляют собой два семейства взаимно перпендикулярных прямых линий.

Нормальной картографической сеткой проекции Меркатора является сетка географических меридианов и параллелей, а нормальной системой сферических координат — географические координаты φ и λ.

Географическая система координат

Положение точки на любой поверхности или в пространстве определяется совокупностью конкретных величин, называемых координатами. Координаты могут выражаться как в линейной, так и в угловой мере; они определяют положение координатных линий относительно принятых за начало осей координат. Для определения положения точек на земной поверхности могут применяться различные системы координат: географическая, прямоугольная, полярная и др. Наиболее употребительной является система географических координат.

Малая ось эллипсоида пересекает поверхность последнего в двух точках, которые называются северными и южным полюсами. Плоскости, проходящие через ось вращения Земли, называются плоскостями земных меридианов, которые в сечении с поверхностью Земли образуют большие круги, называемые меридианами. Плоскость, перпендикулярная земной оси и проходящая через центр эллипсоида, называется плоскостью экватора. Большой круг, образующийся от пересечения этой плоскости с поверхностью эллипсоида, называется земным экватором. Плоскости, параллельные плоскости земного экватора в сечении с поверхностью Земли, образуют малые круги, называемые земными параллелями.

Координатными осями системы географических координат приняты: экватор и один из меридианов, принимаемый за начальный; координатными линиями являются земные параллели и меридианы, а величинами, определяющими положение точек, т. е. координатами, географическая широта и географическая долгота.

Географической широтой точки на поверхности Земли называется угол между нормалью к поверхности эллипсоида в этой точке и плоскостью экватора. Географическая широта в кораблевождении обозначается греческой буквой φ (фи). Счет широт ведется от экватора к полюсам от 0 до 90°. Широты северного полушария считаются положительными и при аналитических расчетах они принимаются со знаком плюс. Северные широты обозначаются буквой N. Широты точек южного полушария, обозначаемые буквой S, считаются отрицательными и им приписывается знак минус. Географическая широта определяет положение параллели, на которой находится определяемая точка.

Географической долготой точки называется двугранный угол, образованный плоскостью начального меридиана и плоскостью меридиана, проходящего через эту точку. Двугранный угол измеряется сферическим углом при полюсе между начальным меридианом и меридианом определяемой точки или численно равной ему дугой экватора, заключенной между названными меридианами. За начальный меридиан в принципе может приниматься любой земной меридиан. По международному соглашению 1884 г. большинством стран мира, в том числе и Советским Союзом, за начальный принят меридиан, проходящий через Гринвичскую обсерваторию, расположенную около Лондона. Счет географических долгот ведется к востоку и западу от Гринвичского меридиана от 0 до 180°. Географическая долгота в кораблевождении обозначается греческой буквой λ (ламбда). Долготы точек, находящихся в восточном полушарии, принято считать положительными (знак плюс), западные долготы считаются отрицательными (знак минус). При определении долготы той или иной точки земной поверхности обязательно указывают на ее наименование: восточной — Оst или, как сейчас принято, Е, западной — W. В зависимости от метода вычисления- географических координат различают координаты геодезические и астрономические.

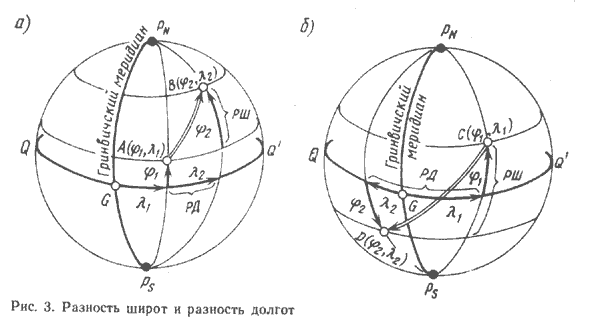
Разность широт и долгот

Географические координаты — широта и долгота — однозначно определяют положение конкретной точки земной поверхности. Переход от одной точки земной поверхности к другой сопровождается изменением их географических координат. Точки, лежащие на одной параллели, имеют одинаковую широту и разные долготы. Точки, расположенные на одном меридиане, имеют одну и ту же долготу и различные широты. В общем случае две точки, не находящиеся на одном меридиане или на одной параллели, имеют разные широты и разные долготы. В практике кораблевождения часто необходимо знать, как изменились или изменятся географические координаты при переходе из одной точки земной поверхности в другую, и уметь вычислять эти изменения. Величинами, характеризующими изменение географических координат при переходе от одной точки земной поверхности к другой, являются разность широт и разность долгот.

Разностью широт (РШ) двух точек на поверхности Земли называется дуга меридиана, заключенная между параллелями этих точек.

Для вычисления разности широт пользуются формулой

РШ = φ₂ - φ₁,

принимая во внимание при этом знаки + и - соответственно их наименованию. Действительно, на рисунке видно, что изменение широты (РШ) при переходе корабля из точки А в точку Б характеризуется дугой А'Б, численно равной разности дуг меридианов точек прихода Б и отхода А, определяемых соответственно широтами φ_Б и φ_А.

Рассчитанной по формуле разности широт приписывается знак плюс, если она совершена к N, и знак минус, если разность широт совершена к S. Разность широт может изменяться от 0 до ±180°.

Разность долгот (РД), характеризующая изменение долготы, как видно из рисунка, представляет собой центральный угол между меридианами двух точек. Этот угол измеряется дугой экватора между указанными меридианами. На этом основании разностью долгот двух точек на поверхности Земли называется меньшая из дуг экватора, заключенная между меридианами этих точек. Из этого определения следует, что разность долгот может иметь значения от 0 до ±180°. С учетом ранее принятых обозначений (для восточной долготы знак плюс и для западной — минус) можно написать формулу для вычисления РД двух точек:

РД = λ₂ - λ₁

Разность долгот будет иметь знак плюс, если она совершена к Ost, и знак минус, если она совершена к W. Указанное правило имеет следующий геометрический смысл: если меридиан пункта прихода λ 2 располагается восточнее меридиана пункта отхода λ 1, значит, разность долгот сделана к Оst и ей приписывается знак плюс. И наоборот, когда меридиан пункта прихода расположен западнее меридиана пункта отхода, разность долгот сделана к W и ей приписывается знак минус.

При решении задачи на расчет РД по формуле может получиться результат, превышающий 180°. В этих случаях для нахождения меньшей из дуг экватора полученный результат следует вычесть из 360° и изменить знак (наименование) его на обратный.