Ответы на вопросы на госэкзамен геодезия
Оглавление
1 Решение прямой и обратной геодезической задачи на плоскости 2
2 Привязка и координирование береговых СНО 3
3 Изображение рельефа дна на МНК 3
4 Понятие референц-эллипсоида. Особенности меркаторской проекции, применяемой при создании МНК. Географические координаты и их разности. 4
5 Зональная система прямоугольных координат Гаусса – Крюгера 8
6 Основные линии и плоскости референц-эллипсоида 8
7 Метод определения высот береговых знаков 10
8 Системы координат, используемые при выполнении промерных работ 11
9 Уклонение отвесных линий 12
10 Главные радиусы кривизны земного эллипсоида 12
11 Вычисление длины дуги меридиана и параллели 13
12 Взаимные нормальные сечения. Уравнение геодезической линии 13
13 Обратная угловая засечка. Решение задачи Ганзена 14
14 Обратная угловая засечка. Решение задачи Потенота 18
15 Определение координат промерного судна с берега прямой засечкой 19
16 Поперечная равноугольная цилиндрическая проекция Гаусса 21
17 Поправки, вводимые в измеренные глубины при выполнении промера мeтодом эхолотирования 22
18 Определение подробности промера по геоморфологическому признаку 25
19 Зарамочное оформление промерных палншетов в проекции Меркатора и Гаусса 26
20 Обследование банок и мелководья 28
21 Классификация уровенных постов и их характеристика 29
22 Правила определения глубин для нанесения на промерный планшет 29
23 Определение среднего многолетнего уровня поста. Нуль уровенного поста. Нуль глубин. 31
24 Участки земной поверхности, которые можно заменить плоскостью без введения поправки за искажение 32
1Решение прямой и обратной геодезической задачи на плоскости
В геодезии есть две стандартные задачи: прямая геодезичеcкая задача на плоскости и обратная геодезическая задача на плоскости.
Прямая геодезическая задача - это вычисление координат X2, Y2 второго пункта, если известны координаты X1, Y1 первого пункта, дирекционный угол α и длина S линии, соединяющей эти пункты. Прямая геодезическая задача является частью полярной засечки.
Обратная геодезическая задача - это вычисление дирекционного угла α и длины S линии, соединяющей два пункта с известными координатами X1, Y1 и X2, Y2 (рис. 1).
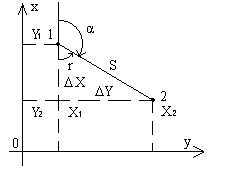
Рис. 1
Построим на отрезке 1-2 как на гипотенузе прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна S, катеты равны приращениям координат точек 1 и 2 ( ΔX = X2 - X1, ΔY = Y2 - Y1 ), а один из острых углов равен румбу r линии 1-2.
Если
Δ X
00
и Δ Y
00,
то решаем треугольник по известным
формулам:
Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому находим:
Общий порядок нахождения дирекционного угла линии 1-2 включает две операции:
определение номера четверти по знакам приращений координат Δ>X и ΔY (рис. 1.4-а),
вычисление α по формулам связи (1.22) в соответствии с номером четверти.
Контролем правильности вычислений является выполнение равенства:
Если ΔX = 0.0 , то
S = ΔY;
и α = 90o 00' 00" при ΔY > 0 ,
α = 270o 00' 00" при ΔY < 0 .
Если ΔY = 0.0 , то
S = ΔX
и α = 0o 00' 00" при ΔX > 0 ,
α = 180o 00' 00" при ΔX < 0 .