1.7 Стійкість пружних систем при комбінованому навантаженні
На
пружну систему можуть одночасно діяти
декілька навантажень, що змінюються
незалежно. Деякі особливості дослідження
стійкості при такому комбінованому
навантаженні продемонструємо на простих
прикладах. Почнемо з системи з одним
ступенем вільності. Розглянемо закріплений
в пружному шарнірі жорсткий стрижень,
на який одночасно діють сили
і
(рис. 1.17 а).
Коли на стрижень діє одна сила
,
то її критичне значення дорівнює
;
аналогічно
.
При одночасній дії сил
і
умова рівноваги відхиленого стрижня
приводить до такого лінеаризованого
рівняння:
З умови існування розв’язків цього однорідного рівняння, що не дорівнюють нулю, знаходимо межу області стійкості
(1.27)
Дійсно,
повторивши міркування, наведені в п.1.5,
і виконавши нескладні перетворення,
неважко встановити, що при
початкове вертикальне положення стрижня
стійке, а при
це положення
нестійке. У координатах
,
межа області стійкості (рис. 1.17 б)
є прямою лінією, що перетинає осі
і
в точках, що відповідають критичним
значенням
і
.
Треба зауважити, що в даному випадку
рівняння межі області стійкості можна
записати у вигляді
а) б)
Рисунок 1.17
Якщо
на систему з одним ступенем вільності
одночасно діють
сил
,
то межа області стійкості буде описуватися
рівнянням
де
- критичне значення сили
,
що діє окремо від інших сил.
Розглянемо пружну систему з двома ступенями вільності, навантажену одночасно силами і (рис. 1.18 а). Умови рівноваги стрижнів в положенні, відхиленому від вихідного, приводять до системи двох лінеаризованих рівнянь:
(1.28)
Прирівнявши до нуля визначник цієї однорідної системи рівнянь, отримаємо рівняння
(1.29)
Припустивши
в цьому рівнянні по черзі, що
і
,
можна знайти критичні значення сил, що
діють окремо:
і
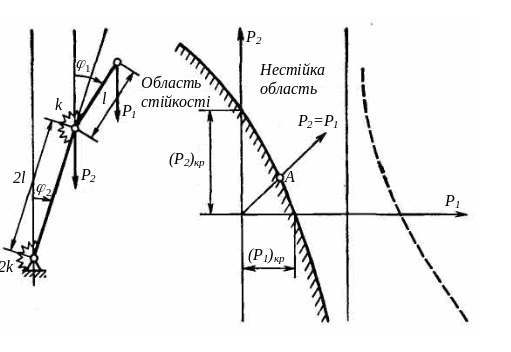
а) б)
Рисунок 1.18
На рис. 1.18 б в координатах , зображена гіпербола, що описується рівнянням (1.29). Найближча до початку координат гілка гіперболи, показана суцільною лінією, є межею області стійкості в даній задачі. Використовуючи наведений в попередньому параграфі шлях, можна довести, що всі точки площини, що лежать зліва від цієї гілки, відповідають стійкому вертикальному положенню стрижневої системи, а точки, що лежать справа, — нестійкому вертикальному положенню. У даній задачі (як і в попередній) межа належить області стійкості.
При
навантаженні сили
і
можуть
зростати пропорційно одному параметру.
У координатах
,
таке навантаження описується променем,
що починається з початку координат.
Так, наприклад, на рис. 1.18 б
зображений промінь, що відповідає
навантаженню
.
Точка перетину променя з межею області
стійкості
відповідає критичній точці біфуркації
початкового положення рівноваги.
У розглянутих вище прикладах межа області стійкості - незамкнена крива, і тому частина променів, що починаються з початку координат, її перетинає, а частина променів не перетинає. У цих випадках можливі такі співвідношення між силами , , при яких втрати стійкості не відбудеться. Але бувають випадки навантаження пружної системи, коли межа області стійкості є замкнутою кривою. Так, для системи, наведеної на рис. 1.19, межа області стійкості буде замкненою кривою.
Рисунок 1.19