1.6 Енергетичний підхід до визначення критичних навантажень. Теорема Лагранжа

Початковий стан рівноваги, розглянутої в попередньому параграфі стрижневої системи (див. рис. 1.14 в), та відомий. Для визначення точок біфуркації потрібно знайти умови існування нових рівноважних станів, суміжних із вихідним. Для цього можна визначити повну потенціальну енергію в стані, суміжному з вихідним. Тоді умова стаціонарності цієї енергії при та повинна привести до визначення точок біфуркації початкового стану. Якщо при цьому повну потенціальну енергію визначити у вигляді розкладання за та , то для визначення точок біфуркації, можливо, не знадобляться високі степені та . Як буде показано далі, для визначення точок біфуркації в розкладанні повної потенціальної енергії необхідно і достатньо врахувати квадратичні доданки стосовно та .

Повна потенціальна енергія складається з внутрішньої енергії деформації і потенціалу зовнішніх сил. Енергія деформації пружних шарнірів при відхиленнях системи на кути та дорівнює

(1.22)

Потенціал зовнішніх сил з точністю до постійного доданка визначається виразом

Обмежившись квадратичними членами розкладання косинусів, остаточно знайдемо

(1.23)

де - це повна потенціальна енергія початкового стану рівноваги, що не залежить від та .

У даній системі з двома ступенями вільності умова стаціонарності повної енергії приводить до таких двох рівнянь:

тобто до тієї самої системи двох лінійних однорідних рівнянь, яка отримана в п.1.5, див. формулу (1.15):

(1.24)

Прирівнявши до нуля визначник цієї системи, можна знайти значення і , що відповідають двом точкам біфуркації, і конфігурації стрижневої системи в околі цих точок (див. рис. 1.14 г, д). У наведеному розв’язку (як і в розв’язку, отриманому вище за допомогою лінеаризованих рівнянь) безпосередньо не фігурувала умова стійкості початкового стану рівноваги. Тому поки не зрозуміло, чому при початковий стан рівноваги є нестійким. Для доведення того, що при переході через першу точку біфуркації початковий стан рівноваги перестає бути стійким, виведемо рівняння (1.24) іншим способом, що базується на теоремі Лагранжа.

Згідно з теоремою Лагранжа консервативна механічна система перебуває у стані стійкої рівноваги тільки тоді, коли її повна потенціальна енергія мінімальна. Таким чином, якщо система перебуває в стійкій рівновазі, то всякі допустимі за умовами закріплення системи відхилення приводять до збільшення її повної потенціальної енергії.

Визначимо зміну повної потенціальної енергії , що відбувається при переході даної системи до нового стану, суміжного з вихідним. Обмежившись квадратичними стосовно та доданками, з виразу (1.23) отримаємо

(1.25)

Якщо початковий стан є стійким, то при будь-яких поєднаннях і повинна виконуватися умова . Ненавантажена система при перебуває в початковому стані стійкої рівноваги, оскільки , де визначається з виразу (1.22). При будь-яких відхиленнях і , що не дорівнюють нулю, умова виконується. Як вже було визначено, критичним називають навантаження , при перевищенні якого початковий стан рівноваги перестає бути стійким. Тому при є такі відхилення, що приводять до . Але при можливі і такі відхилення, що приводять до або до . Відповідно до виразу (1.25) для відхилень, для яких , можна записати таке:

(1.26)

Критичне навантаження можна визначати як найменше значення навантаження, при якому можливі відхилення від початкового стану, що приводять до виконання умови . Неважко переконатися, що необхідна умова мінімуму навантаження , що визначається виразом (1.26), знову приводить до системи рівнянь (1.24). Введемо позначення де

Тоді необхідні умови мінімуму запишуться так:

,

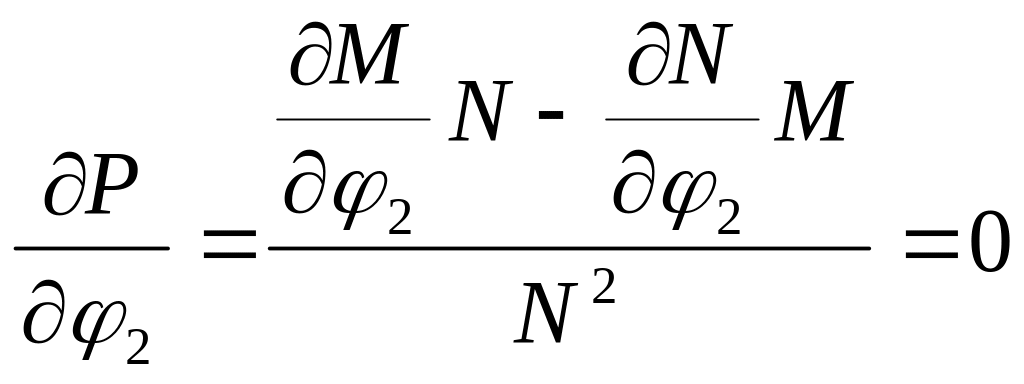або

Оскільки , то можна записати

Знову отримана система рівнянь (1.24), що визначає точки біфуркації початкового стану рівноваги. Але тепер можна стверджувати, що значення , що відповідає першій точці біфуркації, є критичним, тобто в розглянутому завданні .

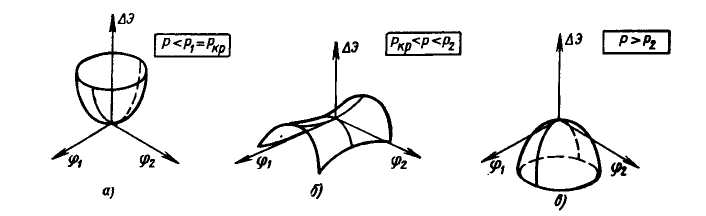
У даній задачі система має дві ступені вільності і відповідно до цього вище знайдено дві точки біфуркації. На рис. 1.16 показана зміна повної потенціальної енергії при відхиленнях системи від початкового стану рівноваги. При повна потенціальна енергія мінімальна, і будь-які відхилення по і приводять до її збільшення (рис. 1.16 а). При початковий стан рівноваги відповідає точці мінімакса повної потенціальної енергії. Цей стан нестійкий, оскільки можливі відхилення системи, що приводять до (рис. 1.16 б). При значення повної потенціальної енергії в початковому стані рівноваги стає максимальним, і будь-які відхилення системи приводять до (рис. 1.16 в). Енергетичний підхід до визначення точок біфуркації і критичних навантажень може бути застосований і в складніших випадках. Для систем з розподіленими параметрами при початковий стан рівноваги завжди відповідає точкам мінімакса повної потенціальної енергії, тобто при будь-яких значеннях повна потенціальна енергія в початковому нестійкому стані не стає максимальною.

а) б) в)

Рисунок 1.16