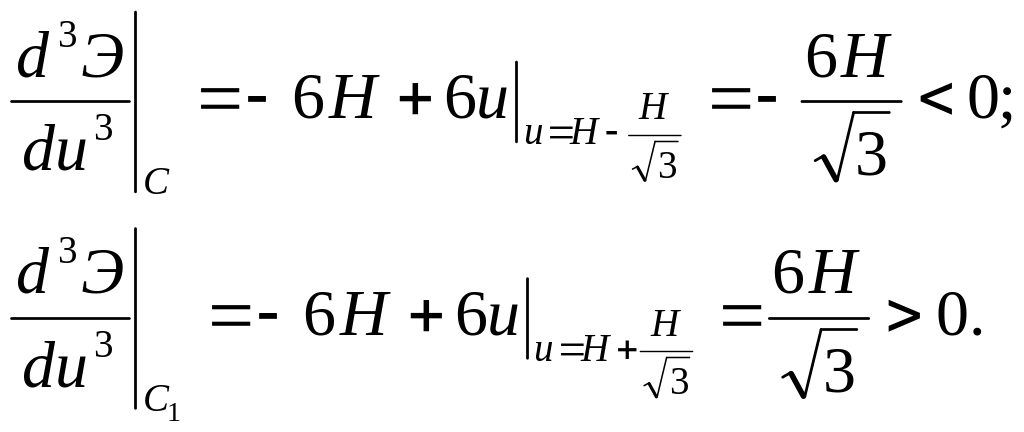1.3 Точки біфуркації, граничні точки і критичні навантаження

Для першого прикладу (рис. 1.5) на діаграмі навантаження – переміщення вісь ординат відповідає початковому вертикальному положенню рівноваги стрижня, а крива - відхиленому положенню рівноваги (рис. 1.10 а). Як встановлено, початкове вертикальне положення залишається стійким до того часу, поки сила . Тому при навантаженні до значення стрижень залишається в початковому вертикальному положенні. При щонайменшому перевищенні вказаного значення початкове вертикальне положення стрижня стає нестійким, і будь-які скільки завгодно малі збурення неодмінно повинні вивести стрижень із цього стану. Оскільки в околі точки , що відповідає рівню навантаження , є інше стійке відхилене положення рівноваги, то стрижень перейде в цей новий стан. На рис. 1.10. а поведінка першої системи при навантаженні схематично зображена стрілками. При стрижень не зможе залишитися в початковому вертикальному положенні і відхилитися вправо або вліво. На діаграмі навантаження-переміщення для першої системи (рис. 1.10 а) характерною є точка , у якій вісь ординат перетинається з кривою , що відповідає відхиленому положенню.

Точки, в яких розв’язок розщеплюється на дві гілки, називаються точками біфуркації, або точками галуження розв’язку.

У даному випадку точка характерна ще і тим, що під час переходу через неї початкове положення рівноваги стрижня перестає бути стійким: точки осі ординат, що лежать нижче точки , відповідають стійким станам, а вище – нестійким. Точки на діаграмі навантаження – переміщення, при переході через які початковий стан рівноваги перестає бути стійким, називаються критичними точками, а відповідні їм значення навантажень – критичними значеннями навантажень, або критичними навантаженнями (критичні навантаження позначатимемо індексом _кр).

а) б)

Рисунок 1.10

Друга система якісно інакше поводиться при дії навантаження. Початкове вертикальне положення стрижня залишається стійким до того часу, поки . У точці біфуркації вісь ординат, що на рис. 1.10 б відповідає початковому положенню рівноваги, перетинається з кривою , яка описує нове нестійке положення рівноваги. Точка критична, оскільки при переході через неї стійке положення рівноваги стає нестійким. Для другої системи критичне навантаження . Досягши цього навантаження, дана система не зможе залишатися в початковому вертикальному положенні, оскільки воно стає нестійким, і будь-які скільки завгодно малі збурення виведуть її з нього. Але на відміну від першої системи у другої немає ніяких нових стійких положень статичної рівноваги в околі критичної точки біфуркації . Тому втрата стійкості початкового вертикального положення рівноваги неминуче супроводжується стрибкоподібним переходом у віддалене на кінцеву відстань нове стійке положення статичної рівноваги (у даному прикладі стрижень просто перекидається). На рис. 1.10 б стрілками показана поведінка другої системи.

Важливо підкреслити, що якщо в першій системі перехід від початкового вертикального положення рівноваги до нового відхиленого положення статичної рівноваги при плавному збільшенні навантаження відбувається плавно без перескоків, то в другій системі навіть плавне збільшення навантаження неминуче супроводжується стрибкоподібним переходом у нове стійке статичне положення рівноваги. (У реальних умовах при такому перескокові виникають коливання стосовно нового стійкого положення статичної рівноваги. І лише після того, як сили опору погасять коливання, система займе нове стійке положення статичної рівноваги. Цей перехідний процес описується з використанням динамічного підходу і в даному курсі не розглядається ).

При розвантаженні дві дані системи поводяться також якісно по-різному. При зменшенні навантаження перша система у зворотному порядку проходить всі етапи навантаження: у точці біфуркації стійке відхилене положення рівноваги змінюється стійким невідхиленим положенням (рис. 1.10 а). Друга система проходить через нову точку біфуркації , де стає нестійким відхилене положення рівноваги. Досягнувши точки біфуркації , система повертається в початкове положення шляхом перескоку (рис. 1.10 б). У таких випадках точку іноді називають верхньою критичною точкою, а відповідне їй значення навантаження — верхнім критичним значенням. Точку називають нижньою критичною точкою, а відповідне їй значення навантаження — нижнім критичним значенням навантаження. Ці значення навантажень відповідно позначимо (або ) і . Так, у розглянутому вище прикладі і .

Надалі траплятимуться критичні точки біфуркації двох основних розглянутих вище типів. У критичній точці біфуркації першого типу початкова стійка форма рівноваги змінюється іншою стійкою формою рівноваги, причому точка біфуркації першого типу відповідає стійкій рівновазі (наприклад, точка на рис. 1.10 а). У критичній точці біфуркації другого типу початкова стійка форма рівноваги змінюється іншою нестійкою формою рівноваги, причому і точка біфуркації другого типу відповідає нестійкій рівновазі (наприклад, точка на рис. 1.10 б).

У загальному випадку можуть бути точки біфуркації й інших типів, наприклад, точки, в яких перетинаються два розв’язки, що відповідають нестійким положенням рівноваги (згідно із наведеним вище визначенням вони не є критичними). Проте точки біфуркації зазначених вище двох типів відіграють першорядну роль в теорії стійкості пружних систем. Критичні точки біфуркації першого типу характерні для задач стійкості пружних стрижнів і пластин, критичні точки біфуркації другого типу — для задач стійкості тонких пружних оболонок. Критичні граничні точки характерні для задач стійкості пологих оболонок і тонких пружних оболонок з початковою геометричною недосконалістю.

Окрім точок біфуркації, в теорії стійкості важливе значення мають граничні точки. У граничній точці різні розв’язки не перетинаються. Проте при переході через неї стійка рівновага стає нестійкою, причому гранична точка, як правило, відповідає нестійкій рівновазі. Відповідно до наведеного вище визначення граничні точки початкової форми рівноваги є критичними.

На рис. 1.11 наведена система двох жорстких стрижнів, з’єднаних шарніром. Повна енергія такої системи дорівнює

,

де .

а) б)

Рисунок 1.11

Тут

Тобто .

З умови стаціонарності повної потенціальної енергії отримуємо залежність переміщення від прикладеного навантаження . Залежність між силою і вертикальним переміщенням точки її прикладання має вигляд кривої, показаної на рис. 1.11 б. Дослідимо стійкість отриманого положення рівноваги

звідки визначаємо положення рівноваги системи .

Показані на рисунку точки та — типові приклади граничних точок, оскільки