1.2 Неоднозначність станів рівноваги пружних систем

При одних і тих самих зовнішніх навантаженнях і умовах закріплення пружна система може мати не один, а декілька станів рівноваги. Покажемо це на найпростіших прикладах. Розглянемо жорсткий стрижень завдовжки , один кінець якого закріплений в пружному шарнірі, а інший навантажений вертикальною силою . У початковому ненавантаженому стані вісь стрижня строго вертикальна. При відхиленнях стрижня сила зберігає вертикальний напрям (рис. 1.5 а). Момент в пружному шарнірі вважатимемо пропорційним куту відхилення стрижня і таким, що дорівнює , де - жорсткість пружного шарніра. Тоді, записавши рівняння рівноваги стрижня у відхиленому від вертикалі стані ( ), отримаємо

. (1.2)

Отримане рівняння має два незалежні розв’язки:

1) при будь – якому значенні ;

2) .

Криві, що відповідають розв’язкам при , показані на рис. 1.5. б, де по осі ординат відкладені значення безрозмірної сили . При єдино можливим буде початкове вертикальне положення рівноваги. При разом з початковим вертикальним положенням рівноваги стрижня ( ) стають можливими й інші положення рівноваги при . Так, наприклад, при можливі три різні положення рівноваги стрижня, що відповідають точкам 1,2 і 3 на рис. 1.5 б. Точка 2 відповідає вертикальному положенню, а точки 1 і 3 відхиленим положенням рівноваги. Якщо розглянути поворот стрижня на довільний кут , то зі зростанням абсолютного значення безрозмірної сили необмежено зростає і число можливих положень рівноваги.

a) б)

Рисунок 1.5

Розглянемо жорсткий стрижень завдовжки , один кінець якого шарнірно закріплений, а на іншому кінці є пружина жорсткості , що зберігає при відхиленнях стрижня горизонтальне положення (рис. 1.6 а). Як і в першому прикладі, до стрижня прикладена вертикальна сила , причому в початковому ненавантаженому стані вісь стрижня строго вертикальна. Вважаючи зусилля в пружині пропорційним її подовженню і, отже, таким, що дорівнює , рівняння рівноваги стрижня у відхиленому положенні запишемо у вигляді

. (1.3)

a) б)

Рисунок 1.6

Це рівняння має декілька незалежних розв’язків:

1) , тобто при будь – якому

, де (1.4)

2) .

На рис. 1.6 б зображений графік за знайденим розв’язком (по осі ординат відкладені значення безрозмірної сили . І в цьому випадку при одному й тому самому значенні навантаження система може мати декілька різних положень рівноваги. Так, при можливі чотири різні положення статичної рівноваги системи, що відповідають .

Очевидно, що інший корінь рівняння (1.3) не дасть нових положень рівноваги. Так, наприклад, відповідатимуть одному й тому самому «перекинутому» положенню рівноваги стрижня і т.д. Тобто навіть на простих прикладах можна показати, що і при одному й тому самому навантаженні й одних і тих самих умовах закріплення система може мати декілька різних положень рівноваги. Слід зазначити, що безліч положень рівноваги може бути виявлена тільки у тому випадку, коли рівняння рівноваги складаються для деформованої відхиленої від свого початкового ненавантаженого положення системи. У лінійній теорії пружності рівняння рівноваги складають для недеформованої системи, тобто використовують «принцип незмінності початкових розмірів» опору матеріалів. В цьому випадку за заданих умов закріплення і заданих зовнішніх навантажень завжди буде виявлено тільки одне положення статичної рівноваги пружної системи. Так, в наведених вище прикладах, складаючи рівняння рівноваги для недеформованої системи, інших положень рівноваги стрижня виявити неможливо, окрім початкового вертикального положення. Для складніших пружних систем число різних можливих положень рівноваги, природно, зростає, а вигляд можливих рівноважних конфігурацій ускладнюється.

Так, наприклад, на рис. 1.7 наведені різні форми рівноваги гнучкого стрижня (природно, вони стають можливими тільки при значних навантаженнях).

Основним завданням теорії стійкості пружних систем є визначення умов, при яких стають можливими різні стани рівноваги системи і встановлення форми рівноважних конфігурацій, з'ясування того, які з цих конфігурацій відповідають стійким станам рівноваги, а які ні.

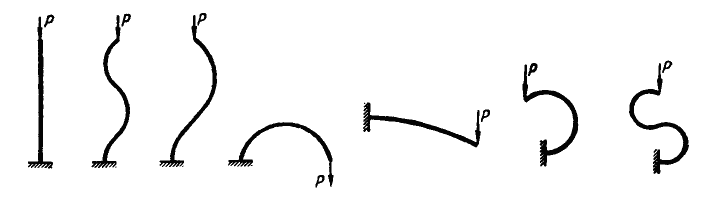
Рисунок 1.7

Для визначення стійкості рівноваги механічної системи необхідно використовувати аналітичні умови стійкості. Найбільш загальним підходом до вивчення стійкості положення рівноваги в механіці є енергетичний підхід, що базується на дослідженні зміни повної потенціальної енергії системи при відхиленнях від положення рівноваги.

У положенні рівноваги повна потенціальна енергія консервативної механічної системи має стаціонарне значення, причому згідно з теоремою Лагранжа положення рівноваги стійке, якщо це значення відповідає мінімуму повної потенційної енергії.

У системах, зображених на рис. 1.1, повна потенціальна енергія змінюється пропорційно вертикальному переміщенню кульки. Коли кулька опускається, її потенціальна енергія, природно, зменшується. Тому нижня точка увігнутої поверхні відповідає мінімуму повної потенціальної енергії, і положення рівноваги кульки в цій точці є стійким. Вершина опуклої поверхні відповідає стаціонарному, але не мінімальному значенню повної потенціальної енергії (у даному випадку – максимальному значенню). Тому положення рівноваги кульки тут є нестійким. Стаціонарна точка на сідлоподібній поверхні також не відповідає мінімуму повної потенціальної енергії (це так звана точка мінімакса), і положення рівноваги кульки тут є нестійким. Останній випадок є одним з найпоширеніших. У нестійкому стані рівноваги потенціальна енергія зовсім не повинна досягати максимального значення. Положення рівноваги не буде стійким в усіх випадках, коли повна потенціальна енергія має стаціонарне, але не мінімальне значення.

Для зображеної на рис. 1.1 б стрижневої системи також неважко встановити, що при дії сили, що розтягує, вертикальне невідхилене положення стрижнів відповідає мінімуму потенціальної енергії і тому є стійким. При стискальній силі невідхилене положення стрижнів відповідає максимуму потенціальної енергії і є нестійким. Читачам пропонується самостійно встановити стійкість систем, показаних на рис. 1.2.

Для систем, наведених на рис. 1.5, 1.6 повна потенціальна енергія пружної системи (з точністю до постійного доданка, яким можна знехтувати) складається із внутрішньої енергії деформації і потенціалу зовнішніх сил :

. (1.5)

Складемо вираз для повної потенціальної енергії стрижня з пружним шарніром, навантаженим силою (рис. 1.5). Енергія деформації пружного шарніра дорівнює . Потенціал зовнішніх сил є роботою сил з переміщення тіла з даного положення в кінцеве, тому в даному випадку з точністю до постійної він дорівнює узятому зі зворотним знаком доданку сили на вертикальне переміщення точки її прикладення, тобто . Отже, повна потенціальна енергія

. (1.6)

Дана система має один ступінь вільності: її деформований стан повністю описується одним незалежним параметром . Тому для дослідження стійкості необхідно узяти похідні від повної потенціальної енергії за (умови стаціонарності). Диференціюючи вираз (1.6), отримаємо

, (1.7)

. (1.8)

Прирівнюючи до нуля першу похідну повної потенціальної енергії, приходимо до рівняння (1.2), яке раніше було отримано безпосередньо з умов рівноваги стрижня і визначає форму рівноваги. Дослідження знака другої похідної дозволяє визначити, які зі знайдених положень рівноваги стійкі.

Дослідимо стійкість положень рівноваги стрижня, що відповідають двом незалежним розв’язкам. Перше з них відповідає вертикальному невідхиленому положенню стрижня при . Згідно із (1.8) для цього положення рівноваги

. (1.9)

При повна потенціальна енергія мінімальна і вертикальне положення стрижня стійке, при повна потенціальна енергія максимальна і вертикальне положення стрижня нестійке. Для дослідження стійкості стрижня у відхиленому положенні підставимо другий з розв’язків (1.2) у вираз (1.8):

. (1.10)

Якщо , то друга похідна повної енергії додатна (оскільки ), і відхилене положення стрижня, яке можливе при , завжди є стійким. З'ясуємо, чи є стійким або нестійким положення рівноваги, що відповідає точці перетину двох розв’язків при та , оскільки в цій точці друга похідна повної енергії дорівнює нулю. Згідно з курсом математичного аналізу в таких випадках для дослідження стаціонарної точки слід використовувати похідні вищих порядків. Послідовно диференціюючи, знаходимо

(1.11)

У досліджуваній точці третя похідна дорівнює нулю, а четверта додатна. Отже, в цій точці повна потенціальна енергія мінімальна, і невідхилене положення рівноваги стрижня при є стійким. Результати проведеного дослідження стійкості різних положень рівноваги стрижня з пружним шарніром показані на рис. 1.8. Там же показана зміна повної потенціальної енергії системи при . Точки відповідають мінімумам повної потенціальної енергії і стійким відхиленим положенням рівноваги; точка - максимуму енергії і нестійкому вертикальному положенню рівноваги стрижня. Графік залежності переміщення від рівня навантаження, як правило, називають діаграмою навантаження – переміщення

Складемо вираз повної потенціальної енергії системи, наведеної на рис. 1.6. При відхиленні стрижня на кут пружина подовжується на величину , а енергія деформації пружини дорівнює . Потенціал зовнішніх сил визначається як і у попередньому прикладі. Таким чином, повна енергія

. (1.12)

Послідовно диференціюючи, знаходимо:

Рисунок 1.8

Прирівнюючи до нуля першу похідну повної потенціальної енергії, отримуємо рівняння рівноваги (1.3). Досліджуючи знак другої похідної, можна визначити, які з положень стрижня є стійкими. Так, для невідхиленого положення при друга похідна повної енергії дорівнює:

Отже, при друга похідна позитивна і вертикальне положення рівноваги стійке; при друга похідна від’ємна і вертикальне положення нестійке. У відхиленому від вертикалі положенні рівноваги, що описується залежністю , друга похідна повної потенціальної енергії дорівнює

.

Таким чином, при друга похідна від’ємна, і відхилене положення рівноваги стрижневої системи є нестійким. Положення рівноваги, що відповідає точкам перетину двох розв’язків (1.4), є нестійкими (наприклад, невідхилене положення стрижня при ). У цьому неважко переконатися, визначивши в цих точках знаки похідних вищих порядків. На рис. 1.9 наведені результати проведеного дослідження і характерні криві зміни повної потенціальної енергії для різних рівнів навантаження. Показаний на простих прикладах метод дослідження стійкості положень статичної рівноваги пружних систем використовують і для складніших систем. З ускладненням пружної системи зростають технічні труднощі його реалізації, але принципова основа – умова мінімуму повної потенціальної енергії - повністю зберігається.

Рисунок 1.9