4.5 Наближені розв’язки основного лінеаризованого рівняння

Задачу стійкості пластин розв’язують за допомогою тих самих наближених методів, що і задачу поперечного вигину пластин [7,8]. Одним із найбільш ефективних методів є метод Гальоркіна. Вище цей метод використовували при розв’язанні одновимірних задач стійкості стрижня (див. п. 2.5 і 3.1). Загальна його схема зберігається і при розв’язанні однорідних рівнянь в частинних похідних.

Розглянемо однорідне лінійне рівняння

(4.48)

де

Граничні умови для , що задані на контурі пластини, теж однорідні. Нагадаємо, що до розв’язання задачі стійкості пластини необхідно визначити її початковий напружений стан, тобто знайти зусилля . При складних контурних навантаженнях і граничних умовах для пластин складної форми, багатозв'язних пластин і в деяких інших випадках ця задача, як правило, може бути розв’язана тільки за допомогою наближеного методу.

При розв’язанні задачі методом Гальоркіна функцію поперечного прогинання візьмемо у вигляді ряду

, (4.49)

де - варійовані параметри; - так звані базисні функції, кожна з яких задовольняє всі задані граничні умови.

Підстановка цього ряду в початкове рівняння (4.48) дає функцію, що тотожно не дорівнює нулю:

.

Через лінійність і однорідність початкового рівняння функція буде лінійною і однорідною щодо варійованих параметрів . Для мінімізації цієї функції необхідно, щоб вона була ортогональна всім базисним функціям тобто виконувалися умови

(4.50)

де інтегрування проводиться за всією площею пластини.

Отримана система рівнянь лінійна і однорідна щодо варійованих параметрів . Для існування нетривіальних розв’язків цієї системи її визначник повинен дорівнювати нулю. Рівність нулю визначника однорідної системи рівнянь приводить до характеристичного рівняння стосовно параметра навантаження . А коренів цього характеристичного рівняння дають приблизно перших власних значень . Для кожного з цих значень з системи (4.50) всі варійовані параметри можна виразити через який – небудь один (наприклад, ) і, використовуючи вираз (4.49), приблизно отримати перших власних функцій

Якщо і система базисних функцій повна, то в границі будуть отримані точні власні значення і всі власні функції задачі. Але, як правило, обмежуються декількома першими членами ряду (4.49), тому питання про повноту системи базисних функцій в даному випадку становить теоретичний, а не практичний інтерес. Наведену схему розв’язання проілюструємо прикладами.

Прямокутна пластина, затиснута по всьому контуру, рівномірно стиснута в двох напрямах (рис. 4.10 а). Граничні умови задачі такі:

при та

при та

Якщо на переміщення пластини в її площині не накладено додаткових зв'язків, то , і рівняння (4.48) набирає вигляду

(4.51)

Вибір апроксимуючої функції – найбільш відповідальний етап наближеного розв’язку. Апроксимуючі функції, з одного боку, повинні задовольняти граничні умови і фізичний зміст задачі, а з іншого боку, повинні бути зручними для математичної обробки. У даній задачі, якщо вважати форму пластини близькою до квадратної, то, враховуючи результати задачі стійкості вільно опертої пластини (п. 4.3), можна чекати, що втрата стійкості защемленої пластини відбуватиметься з утворенням однієї опуклості (рис. 4.10 б). Тригонометричні функції зручні для операцій диференціювання і інтегрування, тому, обмежившись першим членом ряду (4.49), можна прийняти [1]

(4.52)

де

a) б)

Рисунок 4.10

Підставивши цей вираз в рівняння (4.51), знайдемо функцію :

Помноживши функцію на першу базисну функцію і проінтегрувавши за всією площею пластини, отримаємо рівняння

Для існування розв’язків, що не дорівнюють нулю, вираз, що стоїть у фігурних дужках, повинен обертатися в нуль. Ця умова приводить до рівняння, що дає наближені значення критичних співвідношень зовнішніх зусиль

(4.53)

Зокрема, для квадратної пластини ( ), стиснутої в одному напрямі, тобто при , отримаємо де уточнений розв’язок для квадратної пластини дає У цьому випадку для квадратної пластини навіть при збереженні тільки одного члена ряду (4.49) метод Гальоркіна приводить до задовільного результату. При цьому необхідно пам'ятати таке. Обмежившись у розв’язку одним членом ряду, припускаємо одну цілком певну форму втрати стійкості пластини. Для квадратної пластини ця форма близька до дійсної, тому знайдене вище наближене власне значення достатньо близьке до найменшого (критичного) точного власного значення задачі. Зі зміною параметрів пружної системи може відбуватися різка якісна зміна форм втрати стійкості. Тому формула (4.53), що відповідає формі втрати стійкості з утворенням однієї опуклості, при збільшенні відношення може приводити до скільки завгодно великих похибок. З уточненого розв’язку [1] випливає, що при пластина втрачає стійкість з утворенням не однієї опуклості, а двох, при - трьох і т.д. Тому при точність приведеного наближеного розв’язку різко погіршується. Якщо наближений розв’язок потрібно отримати для широкого діапазону зміни параметрів пластини, то при виборі апроксимуючих функцій необхідно передбачити можливість якісної зміни форм втрати стійкості. Наприклад, у даній задачі при функцію прогинань можна взяти у вигляді

де - власні функції задачі стійкості затиснутого обома кінцями стрижня, стиснутого однією силою (див. п. 3.1).

a) б)

Рисунок 4.11

Вільно оперта по контуру нерівномірно стиснута в одному напрямі прямокутна пластина (рис. 4.11 а) при зовнішніх стискаючих зусиллях, що лінійно змінюються за законом де - заданий фіксований параметр.

При цьому

Основне рівняння (4.48) набирає вигляду

(4.54)

Граничні умови задачі:

при та

при та

У рівнянні (4.54) коефіцієнти не залежать від , тому, як і для круглих пластин, можна знайти розв’язок, що задовольняє граничні умови при та :

де - функція координати . Підставивши цей вираз у рівняння (4.54) і скоротивши на , отримаємо

(4.55)

Враховуючи граничні умови при та , при розв’язанні методом Гальоркіна можна задати

(4.56)

Підставивши ряд (4.56) в рівняння (4.55), отримаємо функцію

або

Помноживши знайдену функцію по черзі на всі базисні функції , проінтегруємо від до :

(4.57)

Так, обмежившись тільки одним членом ряду (4.56), отримаємо одне рівняння

з якого в першому наближенні знаходимо

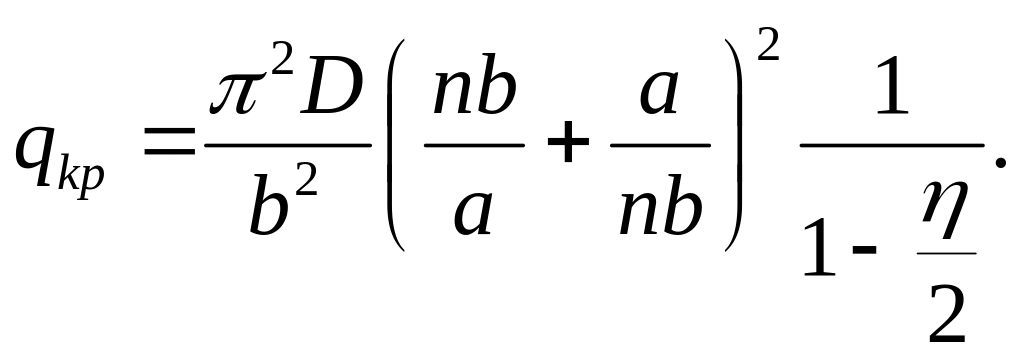(4.58)

Причому число півхвиль у поздовжньому напрямі, що входить в цю формулу, слід підбирати з умови мінімуму , як це зроблено вище для прямокутної пластини, рівномірно стиснутої в одному напрямі. При результат першого наближення збігається з отриманим в п.4.3 результатом точного розв’язку для рівномірно стиснутої пластини. При малих значеннях формула першого наближення (4.58) дає задовільні результати, але зі збільшенням значень її точність різко погіршується; так, при формула (4.58) приводить до абсурдного результату .

Для отримання точнішого розв’язку можна враховувати два перших члени ряду (4.56); тоді система (4.57) складатиметься з двох рівнянь:

Прирівнюючи до нуля визначник цієї системи рівнянь, отримуємо квадратне рівняння для знаходження у другому наближенні:

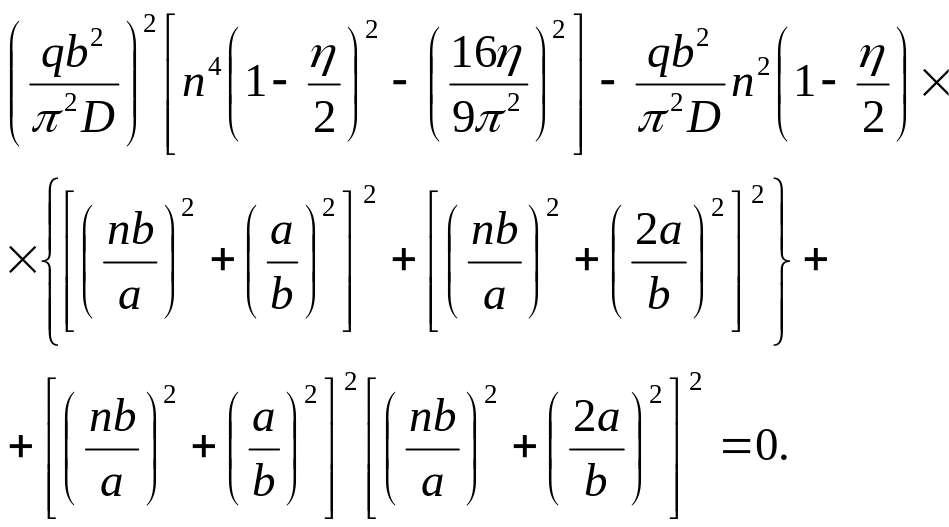(4.59)

Число півхвиль у поздовжньому напрямі для кожного значення , що входить в це рівняння, і відношення слід підбирати з умови мінімуму . Відзначимо, що при частина пластини виявляється стиснутою, а частина – розтягнутою. Відповідно до цього при корені рівняння (4.59) можуть мати різні знаки. Враховуючи велике число членів ряду (4.56), можна отримувати розв’язок в наступних наближеннях. Остаточний результат наводять у вигляді

де - коефіцієнт, що залежить від відношення сторін та параметра . Значення табульовані для всіх практично цікавих випадків [6].

Прямокутна пластина при зсувних навантаженнях (рис. 4.11 б). У цьому випадку і рівняння (4.48) набирає вигляду

(4.60)

Рівняння (4.60) містить змішану похідну , тому навіть для вільно опертої по всьому контуру пластини зі скінченним відношенням сторін точний розв’язок отримати не вдається. Розв’язок рівняння (4.60) в замкнутому вигляді відомий тільки для подовженої пластини при [5]. Остаточний результат цього розв’язку, як правило, записують в такій формі:

(4.61)

Причому при вільно опертих довгих краях пластини а при затиснутих довгих краях

Розглянемо наближене розв’язання для пластини з кінцевим відношенням сторін; контур пластини вважаємо вільно опертим. Скористаємося методом Гальоркіна. Функцію поперечного прогинання візьмемо у вигляді подвійного ряду

(4.62)

Кожен член ряду, очевидно, задовольняє всі задані граничні умови задачі. Для прямокутної пластини з кінцевим відношенням сторін подальше розв’язання, незважаючи на принципову простоту, виявляється громіздким, оскільки точні результати вдається отримати тільки при урахуванні великого числа членів ряду (4.62). Обмежимося розв’язанням в першому наближенні для пластини, близької до квадратної, тобто при . Відмітимо, що навіть в першому наближенні необхідно враховувати два члени ряду (4.62), оскільки, узявши один член ряду, отримаємо умову ортогональності (4.50), що не містить зовнішнього навантаження . Отже, візьмемо

Підставивши цю функцію в рівняння (4.60), знайдемо функцію

Умови ортогональності (4.50) приводять до двох рівнянь:

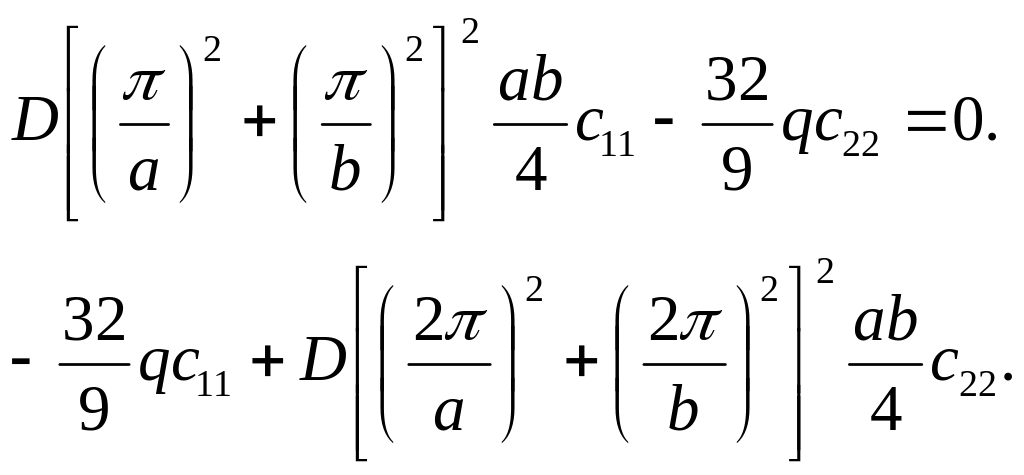(4.63)

Прирівнюючи до нуля визначник цієї системи рівнянь, знаходимо

,

або для квадратної пластини при

(4.64)

де

При цьому значення з рівнянь (4.63) знаходимо

Отже, форма зігнутої серединної поверхні пластини при втраті стійкості приблизно описується функцією

Знаки « »,що входять в отримані вище залежності, відображають той очевидний факт, що зміна напряму зовнішнього контурного навантаження не впливає на її критичне значення. Уточнене значення коефіцієнта у формулі (4.64) для квадратної пластини таке [1].

Врахувавши більше число членів ряду (4.62) і виконавши трудомісткі обчислення, можна знайти значення коефіцієнта у формулі (4.64) і при інших значеннях відношення . Аналогічні розв’язки отримані при інших закріпленнях країв пластини, причому результати цих розв’язків табульовані [6]. Методом Гальоркіна можуть бути розв’язані (і розв’язані) багато інших задач стійкості прямокутних і круглих пластин. Але при всіх перевагах цей метод не можна вважати універсальним методом розв’язання задач стійкості пластин. Основний недолік методу Гальоркіна пов'язаний з необхідністю задоволення всіх граничних умов при виборі базисних функцій. Геометричні граничні умови можна задовольнити порівняно легко, але навіть для пластин простої форми важко вибрати базисні функції, що зручні для математичної обробки і задовольняють усі силові граничні умови. Наприклад, у задачах стійкості прямокутних пластин з одним вільним краєм надзвичайно важко підібрати зручну систему базисних функцій, що задовольняють граничні умови на вільному краю. Це зауваження стосується і пластин з пружно закріпленим краєм або пластин з отворами. В усіх задачах такого роду наближений розв’язок зручніше отримувати енергетичним методом.

Список використаної літератури

1. Алфутов Н.А. Основы расчета на устойчивость упругих систем. – М.: Машиностроение, 1978. – 312 с.

2. Болотин В.В. О сведении трехмерных задач теории упругой устойчивости к одномерным и двумерным задачам./В кн.: Проблемы устойчивости в строительной механике. - М.: Стройиздат, 1965 - С. 186-196.

3. Галлагер Р. Метод конечных элементов. Основы.-М.:Мир, 1984. – 428 с.

4. Зенкевич О.К., Морган К. Конечные элементы и аппроксимация. – М.: Мир, 1987. – 312 с.

5. Пановко Я.С. Губанова И.И. Устойчивость и колебания упругих систем. – М.: Наука 1987. – 436 с.

6. Прочность, устойчивость, колебания: Справочник /Под ред. И.А. Биргера, Я.С. Пановко. - М.: Машиностроение, 1968. –Т.3. – 567 с.

7. Тимошенко С.П. Устойчивость упругих систем.- М.: Гостехиздат, 1946. - 532 с.

8. Тимошенко С.П. Курс теории упругости. – К.: Наукова думка,1972. – 508 с.

Список рекомендованої літератури

1. Вольмир А.С. Устойчивость деформируемых систем. – М.:Наука, 1967. – 984 с.

2. Динник А.Н. Устойчивость упругих систем. - М.: ОНТИ, 1935. – 183 с.

3. Коллатц Л. Задачи на собственные значения. – М.: Наука, 1968. – 503 с.

4. Лурье А.И. Теория упругости. – М.: Наука, 1970. – 940 с.

5. Циглер Г. Основы теории устойчивости конструкций. – М.: Мир, 1971. – 192 с.