4.4 Розв’язання основного рівняння для круглих пластин

У разі осесиметричного початкового напруженого стану круглої пластини, коли , а початкові зусилля та є функціями тільки радіуса , інтегрування загального рівняння (4.27) зводиться до інтегрування звичайних диференціальних рівнянь. У полярній системі координат основне лінеаризоване рівняння для пластини, навантаженої контурними зовнішніми зусиллями, набуває вигляду (див. п. 4.2)

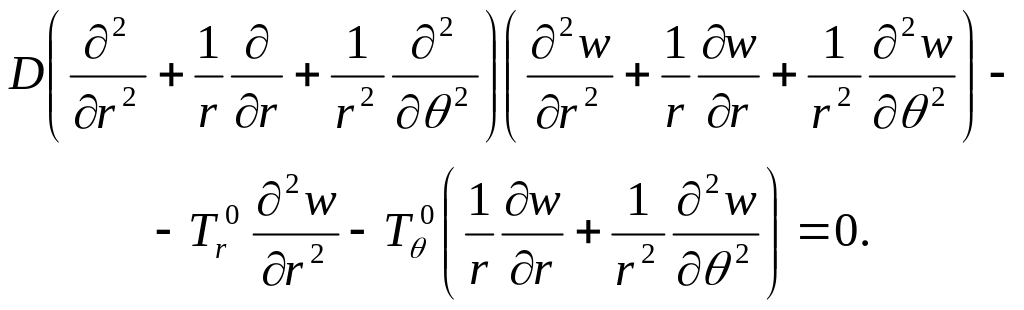(4.39)

У це рівняння входять тільки парні похідні по окружній координаті , тому розв’язок рівняння (4.39) можна знайти у вигляді ряду [1]:

(4.40)

де - деякі функції координати . При цьому граничні умови можуть бути довільними, але незмінними по всьому контуру пластини. Підстановка виразу (4.40) в рівняння (4.39) приводить до системи звичайних незалежних диференціальних рівнянь

(4.41)

Розв’язок цих рівнянь, що задовольняє задані граничні умови, дає власні функції і власні значення задачі; а найменше з власних значень параметра навантаження буде критичним. Рівняння (4.41) найпростіше інтегрується при постійних стискаючих початкових зусиллях та (рис. 4.8):

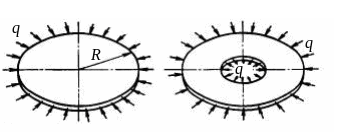
Рисунок 4.8

У цьому випадку рівняння (4.41) матимуть вигляд

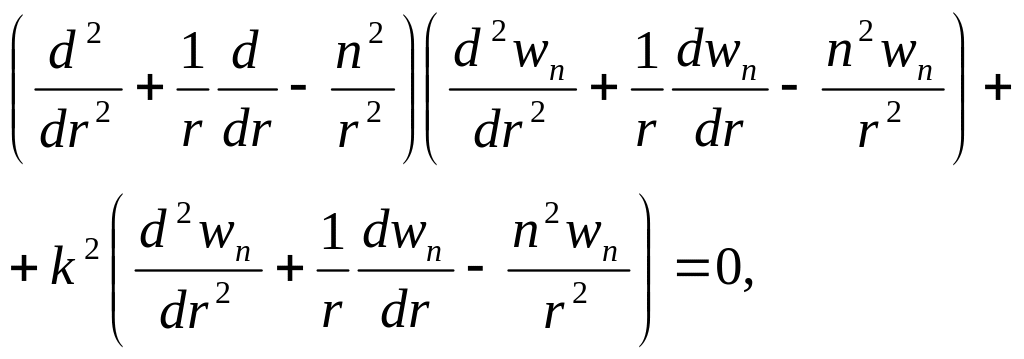(4.42)

де

При осесиметричній формі втрати стійкості (при ) розв’язок рівняння (4.42) має вигляд

при неосесиметричній формі втрати стійкості, коли ,

,

де та - функції Бесселя першого і другого роду (ці функції табульовані). Подальше розв’язання задачі не викликає ніяких труднощів. Розглянемо декілька прикладів.

Суцільна пластина рівномірно стиснута по контуру (рис. 4.9). Незалежно від способу закріплення контура прогинання і кути повороту в центрі суцільної пластини не повинні обертатися в нескінченність. Тому, як і в теорії пружності при вигинанні пластин, для осесиметричної і неосесиметричної форм втрати стійкості необхідно взяти та оскільки , та , при Тобто розв’язок для суцільної пластини спрощується

(4.43)

a) б)

Рисунок 4.9

Якщо контур пластини затиснутий (рис. 4.9 а), то граничні умови на цьому контурі при

Підпорядкувавши розв’язок (4.43) цим граничним умовам, отримуємо однорідну систему рівнянь щодо довільних постійних та :

Рівність нулю визначника цієї системи дає рівняння

(4.44)

Функції Бесселя першого роду пов'язані між собою диференціальним співвідношенням

тому

При з рівняння (4.44) отримаємо

(4.45)

Корені отриманого характеристичного рівняння дадуть власні значення параметра , що є функцією зовнішнього зусилля . Для визначення критичного навантаження необхідно обчислити найменше власне значення параметра , тому для кожного досить знайти перший корінь рівняння (4.45).

Так, для знаходимо ; для - перший корінь і т.д. Отже, для суцільної пластини із затиснутим зовнішнім контуром найменше власне значення дає перший корінь рівняння (4.45) при , тобто

(4.46)

Втрата стійкості затиснутої по контуру пластини відбувається за осесиметричною формою, і вид вигнутої серединної поверхні (рис. 4.9 а) описується (з точністю до постійного множника) функцією, що знаходиться з (4.43) при та :

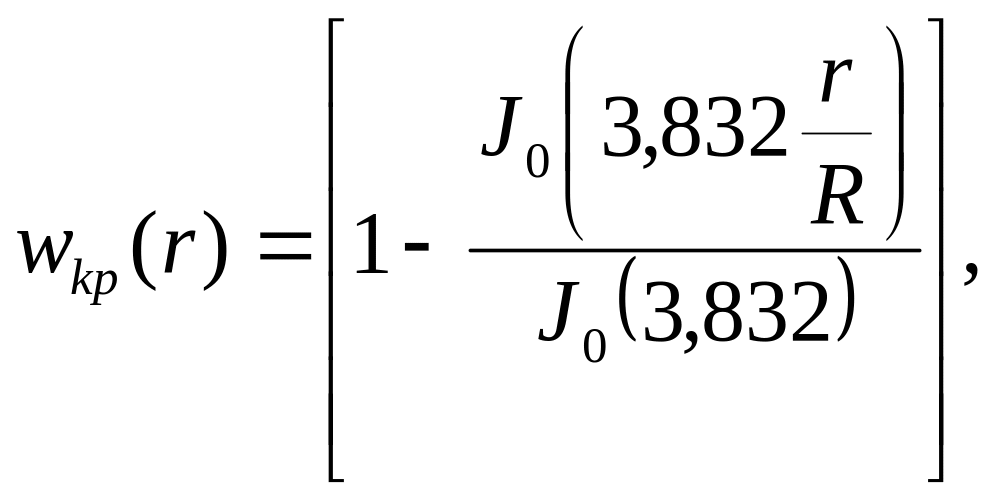
з першої граничної умови при випливає

Якщо край пластини вільно опертий (рис. 4.9 б), то при граничні умови мають вигляд і приводять до граничних умов для функцій

.

Підпорядкувавши рівняння (4.43) цим граничним умовам, знову отримуємо однорідну систему рівнянь стосовно невідомих і . Нескладний аналіз, подібний до проведеного вище, показує, що втрата стійкості вільно опертої пластини теж відбувається за осесиметричною формою, оскільки саме цій формі прогинання пластини відповідає найменше власне значення . Відповідне критичне навантаження

(4.47)

На відміну від випадку затиснутої пластини для вільно опертої пластини коефіцієнт залежить від коефіцієнта Пуассона , який входить до другої граничної умови. При цей коефіцієнт дорівнює

Аналогічний розв’язок неважко отримати і у випадку пружного закріплення контура пластини. Причому остаточну розрахункову формулу можна привести до вигляду (4.47), де змінюється залежно від жорсткості пружного защемлення в межах від 14,68 (абсолютно жорстке защемлення) до 4,2 (вільне обпирання при ).

Стійкість рівномірно стиснутих кільцевих пластин теж може бути досліджена за допомогою рівняння (4.42). Але в цьому випадку розв’язок виходить значно громіздкішим: у виразах для залишаються всі чотири довільні постійні, і підпорядкування цих виразів граничним умовам на внутрішньому і зовнішньому контурах пластини приводить до системи чотирьох однорідних рівнянь. Остаточний результат подається теж у вигляді формули (4.47). У цій формулі для кільцевих пластин коефіцієнт залежить не тільки від граничних умов, але і від відношення внутрішнього і зовнішнього радіусів.