Основне лінеаризоване рівняння
Як це
показано в роботі [1]
рівняння рівноваги елемента у відхиленому
стані не відрізняються від рівнянь
рівноваги елемента в початковому стані
(4.2). Тобто
залишаються такими, що дорівнюють
початковим зусиллям
(з точністю до величин другого порядку
малості).
Виразивши
поперечні сили
та
через внутрішні згинальні моменти за
допомогою залежностей (4.14) і скориставшись
формулами (4.8), рівняння рівноваги
елемента у відхиленому стані можна
записати так:
де
(4.26)
Для пластини постійної товщини отримаємо
(4.27)
Якщо пластина навантажена тільки контурними зовнішніми зусиллями (у силових конструкціях, як правило, власною вагою пластини можна знехтувати), тоді вираз (4.26) можна перетворити до такого вигляду:
При
та
вирази в дужках відповідно до рівнянь
рівноваги (4.2) обертаються в нуль і тоді
(4.28)
Рівняння (4.27) є основним лінеаризованим рівнянням теорії стійкості пластин постійної товщини. Це лінійне однорідне рівняння, причому через перше припущення його граничні умови також однорідні. Якщо вважати, що всі зовнішні навантаження, що діють на пластину, змінюються пропорційно параметру , то рівняння (4.27) можна записати в стандартному вигляді задачі на власні значення:
де
Тут
,
,
- розподіл початкових зусиль при
Таким
чином, задача визначення умов існування
згинальних станів рівноваги плоскої
пластини звелася до типової задачі на
власні значення: потрібно знайти ті
значення параметра навантаження
,
при яких однорідне рівняння має розв’язки,
що не дорівнюють нулю, і що задовольняють
задані однорідні граничні умови. Оскільки
основне рівняння має четвертий порядок,
в кожній точці контура пластини повинні
бути задані дві граничні умови. Для
простоти міркувань обмежимося випадком,
коли ділянка контура пластини збігається
з однією з координатних ліній. Нехай,
наприклад, це буде лінія
Геометричні
граничні умови лінеаризованого рівняння
теорії стійкості пластин не відрізняються
від геометричних умов лінійної теорії
вигину пластин: на краю пластини (в
даному випадку при
)
може бути заборонене поперечне прогинання
і (або) кут повороту
.
Якщо контур пластини вільний від навантажень, то силові граничні умови рівняння (4.27), очевидно, повністю повторюють силові граничні умови лінійної теорії поперечного вигину пластин. Так, наприклад, для вільно опертого краю ( ) силова гранична умова буде
Якщо
врахувати геометричну граничну умову
,
то для вільного опертого краю при
остаточно можна записати такі граничні
умови:
1)
;
2)
.
(4.29)
Якщо
при
край повністю вільний, то
і наведена поперечна сила
тобто на вільному ненавантаженому краї
виконуються такі граничні умови:
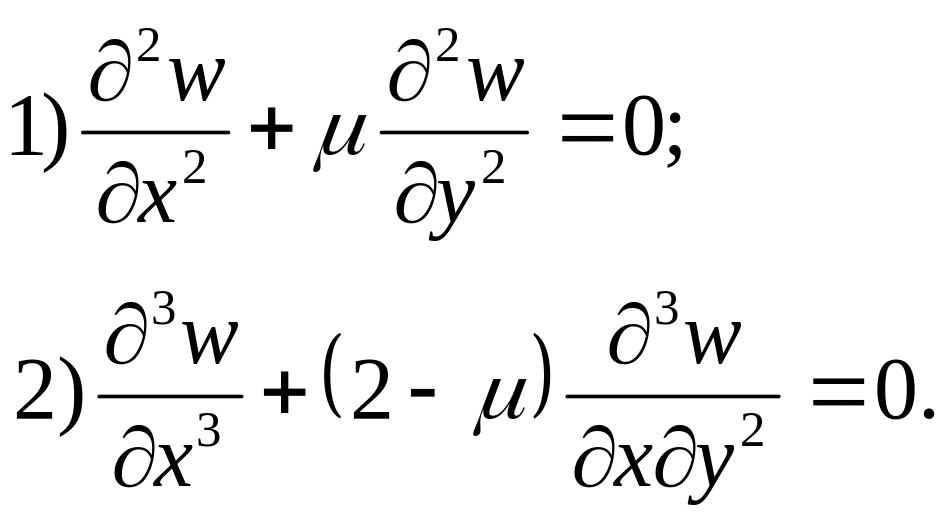
Коли на
краю пластини прогинання повністю
заборонені, зовнішні контурні навантаження
ніяк не відбиваються на граничних
умовах. Наприклад, якщо на вільно опертому
краю
до пластини в її площині прикладені
зовнішні розподілені навантаження
та
,
то ці навантаження не внесуть ніяких
змін до граничних умов вільного обпирання
(4.29). Коли край пластини вільний (або
пружно опертий), зовнішні контурні
навантаження входять в граничні умови
лінеаризованого рівняння [1].
Так, наприклад, розглянемо незакріплений
край пластини
,
навантажений мертвими розподіленими
зусиллями
та
(рис. 4.4).
Рисунок 4.4
Перша
гранична умова, очевидно, залишається
такою самою, як і для ненавантаженого
вільного краю:
Для отримання другої граничної умови
розглянемо рівновагу крайового елемента
пластини з розмірами
та
.
Рівняння рівноваги такого елемента в
проекції на вісь
,
сформульоване для відхиленого стану,
матиме вигляд
Оскільки
при
з (4.4) випливає, що
та
,
другою граничною умовою в даному випадку
буде
Все сказане справедливе і у разі пружнозакріпленого краю пластини, причому для ненавантаженого краю граничні умови лінеаризованого рівняння (4.27) повністю повторюють граничні умови лінійної теорії поперечного вигину пластин.
Основне лінеаризоване рівняння для пластини постійної товщини (4.27), отримане в декартовій системі координат, зручне для розв’язання задач стійкості пластин, контур яких збігається з координатними лініями. Для круглих пластин основне рівняння зручніше подати в полярних координатах.
Лінеаризоване рівняння в новій системі отримаємо шляхом формального перетворення координат, аналогічно до того, як це робиться в курсі «Теорія пружності» [8]. Наприклад, при переході до циліндричної системи координат (рис. 4.5) зовнішній вигляд рівняння (4.27) зберігається:
Але оператор Лапласа має вигляд
Для
основного випадку, коли пластина
навантажена тільки контурними зусиллями,
фіктивне поперечне навантаження
у полярній системі координат визначається
виразом
де
- початкові внутрішні зусилля в серединній
площині пластини в полярній системі
координат (рис. 4.5). Для внутрішніх
моментів в полярній системі координат
маємо такі вирази [8]:
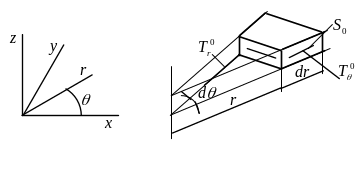
Рисунок 4.5
Неважко записати граничні умови для лінеаризованого рівняння в новій системі координат для кругового контура пластини. Наприклад, для жорстко затиснутого кругового контура граничні умови будуть такі:
Для вільно опертого кругового контура
тобто
