4.1 Поставлення задачі. Основні залежності

Розглянемо пластину в прямокутній системі координат так, щоб її серединна площина збігалася з координатною площиною . Припустимо, що товщина пластини істотно менша інших розмірів пластини в площині (тобто розглядаємо тонкі пластини). Поперечні переміщення точок серединної площини пластини позначимо , переміщення за напрямами осей - відповідно . Пластина навантажена в своїй площині поверхневими і контурними зусиллями , а поперечні навантаження відсутні.

Візьмемо такі припущення.

1. До навантаження пластина ідеально плоска і в докритичному стані рівнодійні всіх зовнішніх навантажень і реакцій опор діють строго в серединній площині пластини.

2. Докритичний напружений стан описується співвідношеннями лінійної теорії пружності і зміною розмірів пластини до втрати стійкості нехтуємо.

3. Всі зовнішні навантаження, що діють на пластину, «мертві», тобто вони не змінюються ні за величиною, ні за напрямом при деформаціях пластини.

4. Вигин пластини описується за допомогою звичайних гіпотез лінійної теорії вигину тонких пластин, тобто гіпотези про нескривлюваність нормалі і гіпотези про малі нормальні напруження в площинах, паралельних серединній площині.

З першого припущення випливає, що завжди можливий плоский стан рівноваги пластини, при якому . Цей невикривлений плоский стан рівноваги вважатимемо початковим і величини, що належать до нього, позначатимемо індексом «0», наприклад, .

Згідно із другим припущенням у початковому стані подовження і кути зсуву в серединній площині пов'язані з похідними переміщень лінійними залежностями Коші

(4.1)

Рівняння рівноваги елемента пластини в початковому невикривленому стані мають вигляд (рис. 4.1)

(4.2)

Початкові внутрішні зусилля в серединній площині , подовження і кути зсуву пов'язані залежностями закону Гука

або в оберненій формі

(4.3)

a) б)

Рисунок 4.1

При заданих граничних умовах на контурі пластини за наведеними залежностями можна визначити напруження і деформації в початковому невикривленому стані. При комбінованому навантаженні на частині контура, на якій діють зовнішні навантаження, граничні умови мають вигляд (рис. 4.1 б)

(4.4)

На іншій частині контура можуть бути задані геометричні граничні умови

(4.5)

У загальному випадку, коли точки контура пластини пружно закріплені щодо зсувів в її площині, граничні умови формулюються так само, як для пружнозакріпленого в поздовжньому напрямі кінця стрижня (див. п. 3.2).

Слід зазначити, що при складних контурах пластини і при складних навантаженнях (наприклад, при зосереджених контурних навантаженнях) визначення початкового напруженого стану пластини є складною задачею. Але коли початковий напружено – деформований стан описується рівняннями лінійної теорії пружності, задачу стійкості можна розв’язувати, не визначаючи цього стану (див. п.2.3).

Надалі припустимо, що всі зовнішні навантаження змінюються пропорційно параметру . Оскільки докритичний напружено – деформований стан описується лінійними рівняннями, можна записати

(4.6)

де - функції, що відповідають розподілу внутрішніх початкових зусиль при

При достатньо малих значеннях параметра навантаження початковий невикривлений стан рівноваги пластини буде єдиним і стійким. Зі зростанням значень параметра у пластини, як і у прямого стрижня (див. розд. 3), можуть з'являтися згинальні стани рівноваги, суміжні з початковим невикривленим станом. Ті значення параметра навантаження , при яких разом з початковим невикривленим станом існують нові згинальні стани рівноваги пластини, визначають точки біфуркації початкового стану рівноваги. Найменше зі значень параметра буде критичним (див. п.1.6). Для визначення точок біфуркації початкового невикривленого стану пластини слід розглядати викривлений стан рівноваги пластини, нескінченно близький до кінцевого, який описуватимемо функцією поперечного прогинання точок її серединної поверхні

(4.7)

де - нескінченно малий параметр, що не залежить від координат; - деяка скінченна функція координат.

При вигині пластини нормаль до її серединної площини повертається в площинах, паралельних координатним площинам та відповідно на кути та . Ці кути з точністю до величини вищого порядку малості щодо параметра пов'язані з поперечним прогинанням співвідношеннями (див. п.1.9)

(4.8)

Зміни кутів уздовж координатних ліній та визначають кривизни деформованої серединної площини в перетинах, паралельних координатним площинам та :

(4.9)

Зміна кута уздовж координати (що дорівнює, через симетричність тензора деформацій, зміні кута уздовж координати ) дає значення кручення деформованої серединної площини

(4.10)

Гауссова кривизна поверхні дорівнює де - головні радіуси кривизни поверхні в даній точці. З точністю до величини вищого порядку малості щодо параметра гауссова кривизна деформованої серединної площини визначається виразом [5]

(4.11)

Нагадаємо, що при чисто згинальних деформаціях поверхні гауссова кривизна залишається незмінною; зокрема, при чисто згинальних деформаціях її кривизна залишається такою, що тотожно дорівнює нулю.

При вигині пластини в ній виникають внутрішні моменти, що вигинають , момент, що скручує , і внутрішні поперечні сили (рис. 4.2). Відповідно до четвертого припущення внутрішні моменти виражаються через поперечне прогинання за допомогою формул, відомих з курсу «Теорія пружності» [8]:

(4.12)

тут

- (4.13)

циліндрична жорсткість пластини.

Рисунок 4.2

У лінійній теорії поперечного вигину пластин рівняння рівноваги формулюються для недеформованого стану. Умови рівноваги елемента пластини в недеформованому стані (рівняння моментів щодо його граней (рис. 4.2)) приводять до двох залежностей [1]:

(4.14)

Якщо на пластину діє нормальне розподілене навантаження , то незалежно від зусиль в серединній площині пластини умова рівноваги елемента пластини (проекція на вісь всіх прикладених до елемента пластини сил) приводить до рівняння

(4.15)

Використовуючи залежність (4.14), отримуємо основне рівняння лінійної теорії поперечного вигину пластин. Для пластини постійної товщини це рівняння має вигляд

(4.16)

При виведенні цього диференціального рівняння для викривленої поверхні пластинки дією зсувних та розтягувальних зусиль нехтували. Тому отримані за допомогою цього рівняння розв’язки будуть справедливі лише у тому випадку, коли краї пластинки при згинанні мають змогу вільно переміщуватися у площині контуру і якщо по краях не прикладені нормальні та дотичні зусилля і , що лежать в серединній площині пластинки. При цих умовах малі прогинання пластинки не будуть супроводжуватися деформаціями у серединній площині, і рівняння (4.16) буде з достатньою для практики точністю визначати викривлену поверхню пластинки. У тому випадку, коли вільні переміщення країв пластинки в площині контуру неможливі або по краях прикладені зусилля і , вигин пластинки супроводжується деформаціями серединної площини. Коли відповідні цим деформаціям напруження малі, їх можна безпосередньо додати до напружень вигину, отриманих з розв’язку рівняння (4.16). Інакше необхідно оцінити вплив цих напружень на вигин пластини.

Відповідне диференціальне рівняння для вигнутої поверхні пластинки можна отримати шляхом таких міркувань. Нехай лінія (рис. 4.3 a) відповідає перетину серединної поверхні вигнутої пластинки з площиною, що паралельна , а - нескінченно малий елемент, що вирізаний з пластинки. Неважко визначити , що зусилля , що прикладені до двох протилежних сторін елемента, дадуть в напрямку осі таку складову:

. (4.17)

Аналогічно зусилля дадуть в напрямку осі складову

. (4.18)

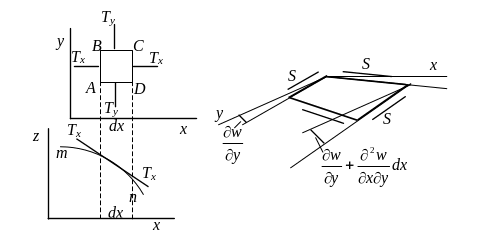
а) б)

Рисунок 4.3

Як це випливає з рис. (4.3 б), зсувні зусилля дадуть

. (4.19)

При виведенні рівняння рівноваги цього елемента складові (4.17-4.19) необхідно додати до навантаження , прикладеного до виділеного елемента пластинки. Тобто прогин пластинки при дії нормального навантаження та зусиль і буде таким самим, як і прогин пластинки під дією одного тільки нормального навантаження з інтенсивністю

.

Отже, в загальному випадку диференціальне рівняння для викривленої поверхні пластинки матиме вигляд

. (4.20)

Як правило, рівняння (4.20) використовують у тих випадках, коли потрібно врахувати вплив зусиль і на прогин пластинки. Найбільш легко ця задача розв’язується, коли і є постійними в серединній площині.

Наведені вище залежності належать до лінійної теорії вигину пластин. Як показано в наступному параграфі, використовуючи ці залежності, можна отримати лінеаризоване рівняння, що дає можливість знайти точки біфуркації початкового невикривленого стану рівноваги пластини і визначити згинальні форми рівноваги пластини в околі точок біфуркації. Але цих залежностей недостатньо для того, щоб досліджувати поведінку пластини в закритичній області при скінченних поперечних прогинаннях. Недостатньо їх і для дослідження стійкості пластин енергетичним методом. Для цих цілей, окрім наведених лінійних залежностей, необхідно використовувати геометрично нелінійні співвідношення теорії гнучких пластин.

Так, значення подовжень, пов'язаних з поперечним прогинанням, як це показано в [1], визначаються за формулами

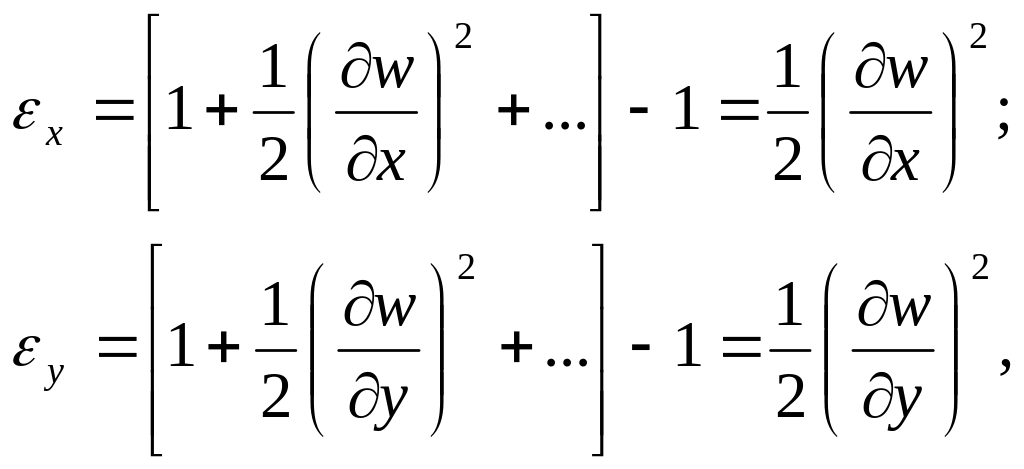(4.21)

а кути зсуву серединної площини, пов'язані з прогинанням ,

(4.22)

Тобто пов'язані з поперечним прогинанням подовження і зсуви серединної площини пластини мають другий порядок малості, тому в лінійних задачах вигину пластини ними нехтують. Якщо, окрім поперечних прогинань , врахувати переміщення у площині пластини, то деформації серединної площини, що викликаються цими переміщеннями, можна підрахувати за лінійними залежностями (4.1), оскільки при вигині тонких пластин можна вважати, що .

Остаточно беремо

(4.23)

Зупинимося на умові нерозтяжності серединної площини пластини. Переміщення та часто виражають через поперечне прогинання з умови рівності нулю значень , що визначаються за формулами (4.23), тобто з умови

(4.24)

Проте для визначення двох функцій та умова (4.24) дає систему трьох рівнянь. Тому переміщення та з цієї системи можна визначати тільки при виконанні деякої додаткової умови, яку можна отримати, виключаючи та . Диференціюючи 2 рази перше рівняння системи (4.24) по , друге – 2 рази по та третє – по та , а потім віднімаючи два перші результати з останнього, отримуємо

(4.25)

Порівнюючи з формулою (4.11), можна зробити висновок, що для визначення переміщень та умовою нерозтяжності серединної площини можна користуватися тільки у тому випадку, коли гауссова кривизна деформованої серединної площини пластини залишається такою, що тотожно дорівнює нулю, тобто коли пластина згинається по так званій поверхні, що розгортається. Наприклад, чисто згинальні деформації, при яких , можливі для пластини з вільним контуром (аркуш паперу можна скрутити в конус). Але треба підкреслити, що в загальному випадку деформації пластини умовою нерозтяжності серединної площини для визначення переміщень та користуватися не можна.