3.7 Вплив початкової неправильності на поведінку стиснутих стрижнів

Розглянуті задачі стійкості стрижнів базувалися на припущеннях, що вісь стрижня до навантаження ідеально пряма, і всі зовнішні сили і реакції опор діють строго уздовж осі. Саме через ці припущення при будь-якому рівні навантажень була можлива прямолінійна форма рівноваги стрижня з поперечним вигином, що тотожно дорівнює нулю. І саме ці припущення приводять до існування критичних навантажень, тобто таких навантажень при перевищенні яких початкова прямолінійна форма рівноваги стрижня перестає бути стійкою. Але вісь реального стрижня не є ідеально прямою і до навантаження є початкові поперечні прогинання, що не дорівнюють нулю. З'ясуємо, як ці початкові прогинання впливають на поведінку стрижня при поздовжньому навантаженні.

Критична точка біфуркації початкової форми рівноваги ідеально прямого стрижня є точкою біфуркації першого типу (див. п. 1.3) і згинальна форма рівноваги в околі критичної точки біфуркації стійка. У тих випадках, коли ідеально правильна система має критичну точку біфуркації першого типу, вплив початкової неправильності можна оцінити за допомогою лінеаризованих неоднорідних рівнянь.

Загальну схему розв’язання покажемо на простому прикладі. Розглянемо шарнірно – опертий стрижень, стислий силою (рис. 3.23). До навантаження початкове прогинання стрижня дорівнює додаткове прогинання, що з'являється в результаті подовжнього навантаження, позначимо Тоді повне прогинання дорівнюватиме

Приймемо, що повні прогинання є величинами малими в порівнянні з довжиною стрижня, а осьове зусилля не залежить від поперечних прогинань стрижня. Прирівнюючи момент від зовнішньої сили до внутрішнього моменту, що вигинає, і утримуючи тільки перші ступені поперечних прогинань, запишемо

(3.57)

а) б)

Рисунок 3.23

У перший доданок входить додаткове прогинання , оскільки виникнення внтурішнього згинального моменту пов'язане з додатковим вигином стрижня. У другий доданок входить повне прогинання: плече зовнішньої сили визначається повним прогинанням

Вважаючи початкове прогинання відомим, рівняння (3.57) запишемо у такому вигляді:

(3.58)

Граничні умови задачі:

Розв’язок рівняння (3.58) можна отримати різними способами, але в даній задачі зручніше скористатися методом розкладання за власними функціями. Власні функції однорідної задачі відомі:

Розв’язок неоднорідного рівняння (3.58) шукатимемо у вигляді розкладання за цими власними функціями:

(3.59)

Праву частину рівняння подамо у вигляді ряду за тією самою системою власних функцій:

(3.60)

Підставивши вираз (3.59) і (3.60) в рівняння (3.58) і прирівнявши коефіцієнти при кожній з синусоїд в лівій і правій частинах рівності, отримаємо ряд незалежних рівнянь алгебри

де

звідки знаходимо

(3.61)

Отже,

(3.62)

Повне прогинання дорівнює

(3.63)

Як бачимо з формул (3.61), при амплітуда відповідної гармоніки . Але при стисненні стрижня може бути реалізоване навантаження Отже, в цьому діапазоні значень навантаження може зростати тільки амплітуда першої гармоніки. Незалежно від співвідношення між початковими амплітудами при наближенні навантаження до домінуючою виявиться перша гармоніка. Тому в наближеному розв’язку, як правило, обмежуються урахуванням першої гармоніки і беруть

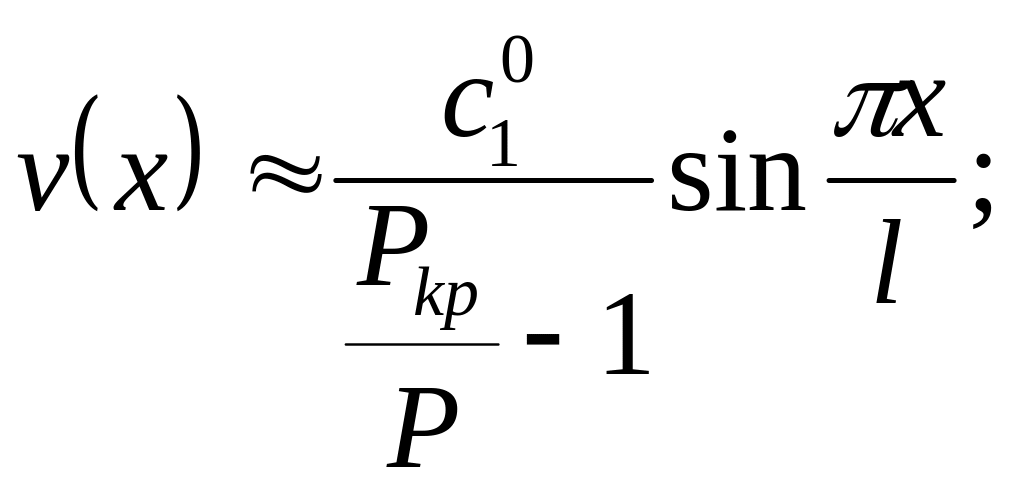(3.64)

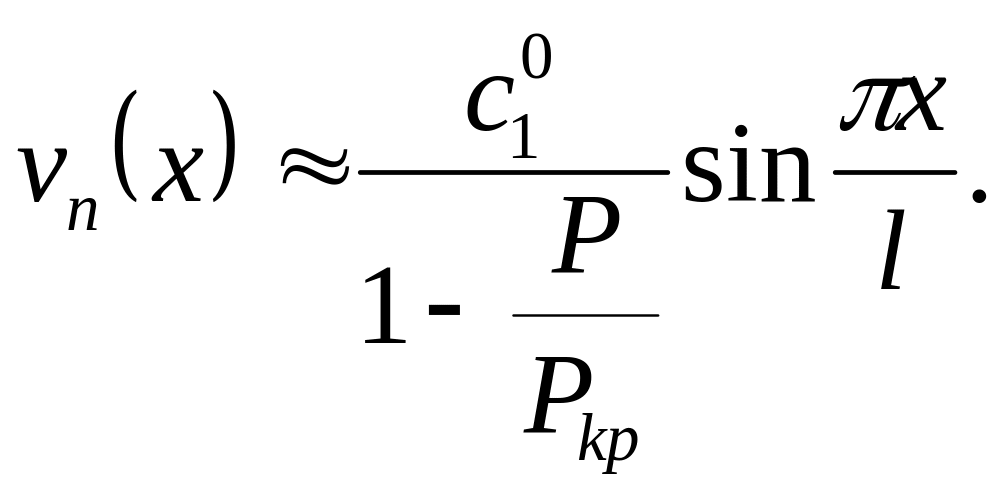(3.65)

Залежність від навантаження показана на рис. 3.23 б.

Визначивши поперечні прогинання, неважко знайти максимальне напруження вигину в стрижні

де - максимальний момент, що вигинає; - момент опору перетину стрижня.

У даному випадку

Повне напруження

(3.66)

де - площа поперечного перетину стрижня. Наприклад, для стрижня прямокутного поперечного перетину, ширина і висота якого відповідно дорівнюють та , отримаємо

Як видно з цієї формули, згинальна складова напруження визначається відношенням амплітуди початкового прогинання до розмірів перетину. Якщо, наприклад, то при максимальне напруження вигину дорівнює напруженню осьового стиснення. Наведений розв’язок можна використовувати і у разі довільного навантаженого стрижня за довільних граничних умов.

Розглянемо довільно навантажений в осьовому напрямі стрижень (рис. 3.24 а), що має початкову неправильність . Нехай при втрата стійкості стрижня описується лінеаризованим однорідним рівнянням

(3.67)

а) б)

Рисунок 3.24

При заданих граничних умовах власні функції цього рівняння і власні значення параметра навантаження вважаємо відомими, причому

(3.68)

Умова рівноваги в проекції на вісь елемента стрижня з початковою неправильністю (рис. 3.24, б) приводить до рівняння

(3.69)

де - повний кут повороту дотичної до осі стрижня, який вважаємо величиною кінцевою, але малою. Як і при виведенні рівняння (3.4), . Внутрішній момент, що вигинає , виникає у результаті додаткових прогинань , тому Тоді рівняння (3.69) набере вигляду

(3.70)

де - малі але скінченні додаткові прогинання. Якщо задача поздовжнього навантаження стрижня статично не визначна, то необхідно враховувати взаємний вплив та Але якщо така задача статично визначена, то можна вважати, що не залежать від поперечних переміщень. Тоді поведінка стрижня з початковою неправильністю описуватиметься неоднорідним лінеаризованим рівнянням

(3.71)

де - розподіл внутрішніх зусиль в стрижні без початкової неправильності при .

Дослідимо докладніше цей найцікавіший в практичному відношенні випадок, коли поведінка стрижня з початковою неправильністю може бути описана рівнянням (3.71). Розв’язок цього рівняння шукатимемо у вигляді розкладання за власними функціями однорідного рівняння (3.67):

Подамо початкову неправильність також у вигляді розкладання

Підставивши ці розкладання в рівняння (3.71), отримаємо

Помножимо обидві частини цього рівняння на власні функції і проінтегруємо від до . Через властивість узагальненої ортогональності

Отже,

Поділимо всі доданки на . З урахуванням виразу (3.68) отримаємо незалежні рівняння для визначення коефіцієнтів :

.

Тоді

.

Як у наведеному вище прикладі, приблизно можна взяти

(3.72)

де - перша власна функція однорідної задачі, що описує форму зігнутої осі ідеально правильного стрижня при втраті стійкості. У наведеному розв’язку передбачалося, що початкова неправильність осі стрижня відома. В цьому випадку, розкладаючи функцію початкового прогинання у ряд за власними функціями , можна знайти і безпосередньо скористатися отриманим результатом.

Ця обставина знижує практичну цінність наведеного розв’язку, оскільки детальне вимірювання початкової форми осі стрижня – операція важкоздійсненна. Проте структура формул (3.64) і (3.72) дозволяє різко спростити і скоротити необхідне число вимірювань при випробуванні реальних стрижнів на осьове стиснення. Так, наприклад, формулу (3.64) для шарнірно опертого стрижня можна переписати у вигляді

(3.73)

де - додаткове прогинання в середньому перетині стрижня (рис. 3.25 а).

Таким чином, між та існує лінійна залежність. Вимірявши при декількох значеннях додаткове прогинання в середньому перетині стрижня , можна експериментально побудувати лінійну залежність, як показано на рис. 3.25 б.

а) б)

Рисунок 3.25

Такий прийом обробки експериментальних даних запропонований Саусвеллом і називається методом Саусвелла. За допомогою цього прийому на реальних стрижнях можна експериментально визначити значення , не проводячи їх попереднього обміру. Для цього, провівши по декількох експериментально отриманих точках пряму, знаходять її перетин з віссю абсцис. Прийом Саусвелла дозволяє за декількома вимірами знаходити амплітуду початкової неправильності . Для цього досить знайти точку перетину побудованої прямої з віссю ординат. Нарешті, прийом Саусвелла дає можливість проводити неруйнуючі випробування стрижнів на осьове стиснення, оскільки, визначивши за початковим етапом навантаження та , можна аналітично прогнозувати подальшу поведінку стрижня під навантаженням (включаючи можливий розвиток пластичних деформацій).

Розділ 4 Стійкість пластин

У цьому розділі подане поставлення задачі стійкості тонкої пружної пластини, розглянуті розв’язки основного рівняння для прямокутних і круглих пластин і наведено наближене інтегрування цього рівняння методом Гальоркіна. Ці класичні розв’язки задач стійкості пластин отримані в кінці XIX – поч. XX ст., проте вони не втратили практичного значення. Їх результати широко використовуються в інженерних розрахунках і служать еталоном для відпрацювання і апробації всіх сучасних наближених методів розрахунку пластин на стійкість.