3.6 Форми рівноваги в закритичних областях

Лінеаризовані рівняння, використані вище при розв’язанні задач стійкості стрижня, дають можливість знаходити власні функції задачі і власні значення параметра навантаження. Найменше власне значення дорівнює критичному значенню навантаження, а відповідна йому власна функція описує форму зігнутої осі стрижня в околі першої точки біфуркації. Але однорідне лінеаризоване рівняння не може дати ніякої інформації про характер критичної точки біфуркації і про поведінку стрижня при прогинаннях після втрати стійкості.

Аналогічно, розв’язуючи задачі стійкості енергетичним методом і обмежуючись у виразі для зміни потенціальної енергії квадратичними стосовно величин поперечних переміщень доданками, знаходили тільки критичні навантаження і відповідні їм власні функції. Характер критичної точки біфуркації і поведінка стрижня при скінченних прогинаннях після втрати стійкості також залишався невідомими. Для того щоб визначити їх, необхідно розглядати задачі стійкості стрижня в нелінійній підстановці.

Задача нелінійної деформації гнучких стрижнів вивчена достатньо повно; у ряді випадків розв’язок вдається отримати у вигляді табульованих функцій. Наприклад, для стрижня постійного поперечного перетину із затисненням, стиснутого силою (рис. 1.4), розв’язок виходить в еліптичних інтегралах. Для того щоб його отримати, скористаємось нелінійним диференціальним рівнянням згинання стрижня:

(3.32)

де знак «+» відповідає у випадку, коли момент спричиняє збільшення кривизни; - максимальний прогин стрижня.

Введемо нову змінну , тоді основне диференціальне рівняння набере вигляду

(3.33)

де .

Граничними умовами цієї задачі є

Скористаємось очевидною рівністю , тоді рівняння згинання стрижня (3.33) набуде вигляду

Останнє рівняння дуже легко проінтегрувати. Його загальний розв’язок має вигляд

Використовуючи третю граничну умову, отримаємо значення постійної

,

тобто . Зробивши нескладні перетворення, отримаємо рівняння з роздільними змінними

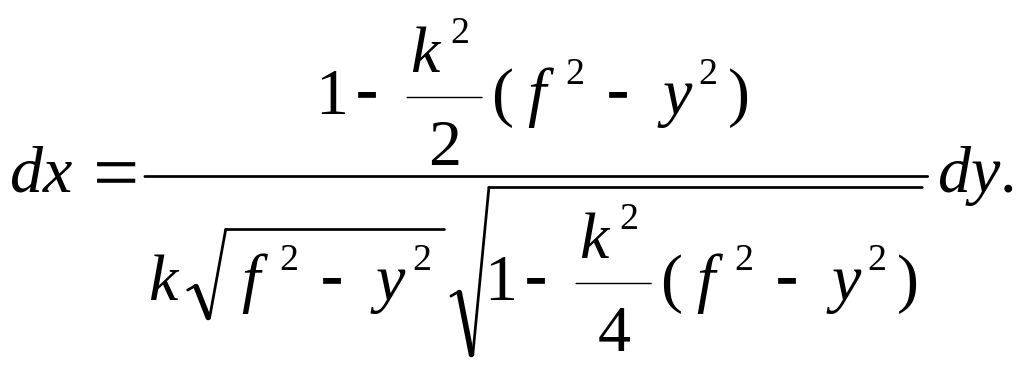
Для того щоб проінтегрувати останній вираз, скористаємось криволінійною координатою . З урахуванням того, що і , матимемо

(3.34)

Введемо нову змінну і константу :

(3.35)

Остання рівність є постійною для кожного окремого значення зовнішнього навантаження і жорсткості стрижня на згинання. Тоді

(3.36)

Після очевидних перетворень диференціальне рівняння (3.34) у нових змінних набере вигляду

. (3.37)

Визначимо граничні умови для нових змінних. На кінцях стрижня маємо

Використовуючи залежності (3.36), матимемо

(3.38)

Інтегруючи (3.37) з урахуванням умов (3.38) ,отримаємо

Використовуючи повний еліптичний інтеграл і вирази (3.35), (3.36), розв’язок цієї задачі запишемо у такому вигляді:

(3.39)

В останній рівності (3.39) знак обирається залежно від того, в який бік відхиляється стрижень при навантаженні.

Таким чином, якщо відоме навантаження стрижня і його жорсткість на згинання, з (3.39) за допомогою табульованих значень еліптичного інтеграла знаходимо постійну , за значенням якої будуємо залежність

Розв’язок (3.39) можна записати по-іншому, якщо взяти до уваги, що для такого стрижня раніше було отримано , тобто Тоді (3.39) набере вигляду

Як вже зазначалося, тільки для деяких умов закріплення кінців стрижня і навантаження можна отримати розв’язок хоча б у вигляді табульованих значень, як це показано вище. Для більшості ж задач стійкості краще використовувати наближений енергетичний прийом розв’язання, що дозволяє досліджувати закритичну поведінку будь-якого довільно навантаженого стрижня, якщо для нього відомий розв’язок лінійної задачі. При цьому обмежимося малими в порівнянні з довжиною стрижня прогинами, оскільки тільки вони становлять інтерес в силових конструкціях.

Розглянемо характерний для більшості практичних задач випадок, коли після втрати стійкості один із кінців стрижня може безперешкодно зміщуватися в поздовжньому напрямі (рис. 3.21).

Тоді закритична деформація полягає у вигині стрижня. При цьому вісь стрижня можна вважати нерозтяжною. З умови нерозтяжності осі стрижня легко виразити поздовжні переміщення через кут нахилу дотичної до пружної лінії. Так, на лівій опорі , а

(3.40)

де - координата, що відраховується від лівої нерухомої опори уздовж деформованої осі стрижня. Внутрішній згинальний момент

(3.41)

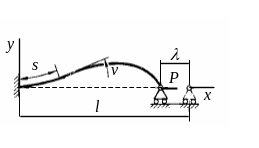
а) б)

Рисунок 3.20

Вирази (3.40) і (3.41) дозволяють підрахувати зміну повної потенціальної енергії стрижня при переході від прямолінійного стану рівноваги до викривленого. Так, наприклад, якщо стрижень навантажений тільки стискаючою силою (рис. 3.20 а), то

(3.42)

Для стрижня, що перебуває під дією тільки розподіленого навантаження (рис. 3.20 б),

(3.43)

Аналогічно можна скласти вираз для будь-якого випадку навантаження стрижня, коли закритичний вигин відбувається без розтягування осі стрижня. Умова стаціонарності визначає рівноважні стани зігнутого стрижня при кінцевих прогинаннях, а дослідження знака другої варіації дозволяє встановити, які з рівноважних станів стійкі. Наведені вище залежності, що описують закритичну деформацію стрижнів з нерозтяжною віссю, є точними (в рамках теорії гнучких пружних стрижнів).

Розв’яжемо цю саму задачу за допомогою метода Релея – Рітца. Вважаємо, що розв’язок лінійної задачі (точний або наближений) отриманий (див. п.3.1, рис. 3.5 а), і, зокрема, відомі критичне навантаження і відповідна йому перша власна функція задачі . Відмітимо, що при розв’язанні задач стійкості в лінійному поставленні відмінність між координатами та зникає і основні функції та можна замінити на та .

При малих, але кінцевих прогинаннях стрижня природно припустити, що в околі першої критичної точки біфуркації форму зігнутої осі стрижня можна апроксимувати першою власною функцією. Тому розв’язання нелінійної задачі в першому наближенні шукатимемо у вигляді

, (3.44)

де - коефіцієнт, що залежить від зовнішнього навантаження; - перша власна функція лінійної задачі. У наближеному розв’язку, коли обмежуємося дослідженням малих відхилень стрижня від прямолінійного положення рівноваги, у виразі (3.40) доцільно розкласти в ряд. Тоді отримаємо

(3.45)

Підраховуючи з використанням (3.44) зміну повної потенціальної енергії стрижня, приходимо до простої залежності . Таким чином, використовуючи метод Релея – Рітца, задачу дослідження закритичної деформації стрижня можна звести до задачі дослідження нелінійної системи з одним ступенем вільності. Так, наприклад, для стрижня, стиснутого однією силою, вираз (3.42) з урахуванням розкладання (3.45) і апроксимації (3.44) набере вигляду

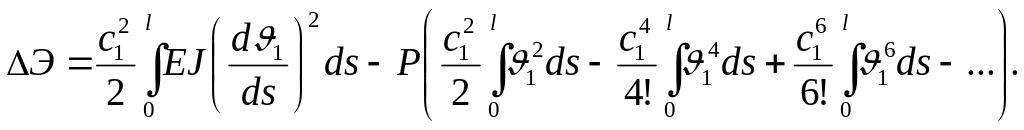Умова стаціонарності (у даному випадку ) приводить до рівняння

Поділивши всі доданки на і враховуючи, що - перша власна функція задачі і, отже, (див. формулу 3.13), приходимо до рівняння

(3.46)

де

. (3.47)

З рівняння (3.46) випливає, що при можлива тільки одна прямолінійна форма рівноваги стрижня, що відповідає При стає можливою й інша форма рівноваги, що описується (приблизно) залежністю (3.44), причому зв'язок між коефіцієнтом та силою виражається рівнянням

(3.48)

Обмежившись в розкладанні (3.45) четвертими степенями та взявши, що отримуємо спрощену формулу

(3.49)

Досліджуючи знак другої похідної неважко встановити, що згинальна форма рівноваги стрижня є стійкою. Критична точка біфуркації є точкою біфуркації першого типу (див. п.1.3). Результат проведеного дослідження зображений на рис. 3.21 а. Аналогічно наближений розв’язок може бути отриманий для стрижня, що перебуває під дією розподіленого навантаження де - параметр навантаження; - розподіл навантаження при . Знову скористаємося апроксимацією (3.44) і отримаємо спрощену формулу для наближеного визначення :

(3.50)

де

(3.51)

Аналіз стійкості прямолінійної і згинальної форм рівноваги аналогічний вищенаведеному.

а) б)

Рисунок 3.21

Необхідно підкреслити, що при різних законах зміни згинальної жорсткості і різних граничних умовах змінюються критичні навантаження і вид власних функцій .

Знаючи, як зміниться кут , легко знайти поперечні прогинання стрижня на ранній закритичній стадії деформації. При нерухомій лівій опорі функція поперечного прогинання визначається виразом

(3.52)

Розкладаючи в ряд і використовуючи залежність (3.44), приблизно знаходимо

(3.53)

У побудованому наближеному розв’язку функція поперечного прогинання залишається подібною до першої власної функції лінеаризованої задачі, а амплітуда прогинання зростає пропорційно коефіцієнту . Тому крива на рис. 3.21 а також характеризує темп зростання поперечних прогинань стрижня при

Отриманий результат можна подати в інших координатах. Замість залежності навантаження – амплітуда поперечного прогинання можна побудувати, наприклад, залежність навантаження – зближення кінців стрижня . Зближення кінців стрижня складається з укорочення стрижня під дією стискаючого навантаження і додаткового зближення кінців, викликаного вигином стрижня. Позначимо , де - зближення кінців стрижня відповідно за рахунок укорочення його осі і за рахунок вигину. При відомому розподілі початкових зусиль значення визначається елементарно. Значення можна знайти за допомогою залежностей (3.44) і (3.45)

Обмежившись другими степенями розкладання, отримаємо

(3.54)

Значення визначаємо залежно від виду навантаження за формулою (3.47) або (3.51). Залежність від стискаючого навантаження показана на рис. 3.21 б. Описаний метод розв’язання може бути використаний і у тому випадку, коли заданими є не навантаження, а зближення кінців стрижня (наприклад, при навантаженні стрижня в жорсткій випробувальній машині). Тоді розрахунок необхідно вести в зворотному порядку: за визначити і потім підрахувати амплітуду поперечного переміщення. При цьому всі отримані вище розрахункові залежності справедливі. Аналогічно можна вести розрахунок в тих випадках, коли задано не зближення кінців стрижня, а підвищення його температури при нерухомо зафіксованих кінцях. Напруження в стрижні після втрати стійкості складається з напруження поздовжнього стиснення і напруження вигину, причому, визначивши форму зігнутої осі стрижня, неважко підрахувати напруження вигину. Остаточно отримуємо

(3.55)

де - момент опору поперечного перетину стрижня.

Схему розрахунку пояснимо на двох прикладах. Розглянемо спочатку закритичну поведінку шарнірно опертого стрижня постійного поперечного перетину, стиснутого однією силою Р. Перша власна функція лінеаризованої задачі відома:

За першою з формул (3.47) знаходимо

З виразу (3.53) отримуємо залежність

При визначенні зближення кінців враховуємо, що

За формулою (3.54) знаходимо

Згідно з виразом (3.55) отримуємо

Очевидно, максимального значення напруження набуває при

Вважаючи, що , можна записати

де

Для квадратного поперечного перетину і формулу для визначення можна переписати таким чином:

З цього виразу видно, що для тонких стрижнів щонайменше перевищення критичного навантаження приводить до появи значного згинального напруження. Так, при перевищення на 1% викликає згинальне напруження, що перевищує більш ніж в 50 разів критичне напруження рівномірного стрижня при .

l

s

q

Рисунок 3.22

Розглянемо закритичну поведінку стрижня, зображеного на рис. 3.22, що втрачає стійкість під дією власної ваги. Критичне навантаження для такого стрижня дорівнює причому форма зігнутої осі стрижня при втраті стійкості описується функціями Бесселя. Але для побудови наближеного розв’язку ці функції незручні. Закритичні переміщення і напруження можна оцінити, використовуючи для опису форми зігнутої осі стрижня простіші функції, що задовольняють задані граничні умови задачі. Наприклад, у даному випадку (див.п. 3.1).

де - координата, що відлічується від затиснення кінця стрижня. Відмітимо, що, враховуючи наближений характер всього розв’язку, функцію можна подати в іще простішому вигляді. Наприклад, у даній задачі, задовольняючи тільки геометричну граничну умову візьмемо

Тоді отримаємо

Максимальне прогинання при приблизно визначається за формулою

Для максимального моменту безпосередньо з умови рівноваги отримаємо наближену формулу

Неважко перевірити, що при спрощенні виду апроксимуючої функції остаточні результати змінюються несуттєво. Якщо закріплення кінців стрижня в поздовжньому напрямі виключать можливість втрати стійкості без розтягування його осі (див. п. 3.3), то наведена вище схема розв’язання не може бути застосована, оскільки вона ґрунтується на припущенні про нерозтяжність осі стрижня. В цьому випадку при підрахунку повної потенціальної енергії стрижня у викривленому стані необхідно враховувати енергію розтягування

де - початкові осьові переміщення і подовження; - додаткові осьові переміщення і подовження, причому

Найбільш простий наближений розв’язок можна отримати, якщо скористатися такими припущеннями:

1) перша власна функція лінійної задачі з точністю до масштабу описує закритичне прогинання стрижня;

2) осьові додаткові переміщення пов'язані з поперечними прогинаннями залежністю (3.20).

Тоді зміна повної потенціальної енергії стрижня при переході в новий відхилений стан рівноваги дорівнює

(3.56)

де - коефіцієнт, що залежить від рівня навантаження; - перша власна функція лінійної задачі, причому, коли

Таким чином, задача про закритичні деформації стрижнів знову зведена до нелінійної задачі деформації системи з одним ступенем вільності. Якщо вважати, що зовнішні навантаження зростають пропорційно одному параметру , то залежності між параметром і параметром навантаження встановлюються з умови в даному випадку з умови Ця залежність матиме таку структуру:

де - коефіцієнт, що залежить від , тобто від жорсткості стрижня на розтягуванні. Характер критичної точки біфуркації такий самий, як і у разі втрати стійкості осі стрижня без розтягування. Але кількісно закритична поведінка стрижня інша: після втрати стійкості поперечні прогинання зростають не так швидко, як при втраті стійкості стрижня без розтягування осі.