3.5 Стійкість стрижнів з урахуванням податливості опор

До цього часу розглядалися пружні стрижні на абсолютно жорстких опорах, хоча насправді будь-яка реальна опора має ту чи іншу податливість. У задачах стійкості однопролітних стрижнів жорсткості пружних опор повинні враховуватися при складанні граничних умов. Наприклад, на рис. 3.15 а показаний стрижень, один кінець якого опертий на пружну опору жорсткості , а інший кінець пружно затиснутий, причому жорсткість затиснення при повороті кінця дорівнює . При формулюванні граничних умов слід розглядати рівновагу кінцевого елемента стрижня у відхиленому стані. Так, проектуючи на вісь всі сили, що діють на елемент стрижня у лівому кінці (рис. 3.15 б), і враховуючи, що переміщення викликає в пружній опорі реакцію при отримуємо таку граничну умову:

a

P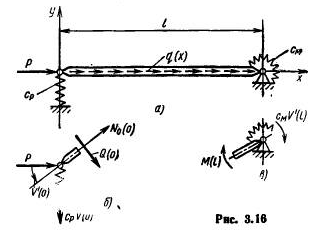

)

б) в)

Рисунок 3.15

З рівності нулю суми моментів, що діють на елемент стрижня у правому кінці (рис. 3.15 в), при отримуємо другу граничну умову оскільки кут повороту викликає в пружному защемленні момент, що дорівнює . Дві інших граничних умови очевидні. Враховуючи, що в даному прикладі , остаточно можна записати такі чотири граничні умови

Подальша загальна схема розв’язання така сама, як і для стрижнів на абсолютно жорстких опорах. Визначимо, наприклад, критичну силу і форму втрати стійкості стрижня, зображеного на рис. 3.16, вважаючи згинальну жорсткість постійною. В даному випадку (пружну основу не вводимо) загальне рівняння (3.4) має вигляд

Рисунок 3.16

Граничні умови для цього стрижня

Загальний розв’язок рівняння має вигляд

Використовуючи граничні умови задачі, випишемо три перші рівняння з трьох перших граничних умов:

Звідси Отже, розв’язок цієї задачі має вигляд

(3.30)

Після визначення власних значень з цього виразу знаходимо відповідні власні функції задачі, причому власна функція, що відповідає критичному значенню , описує форму зігнутої осі стрижня при втраті стійкості. Використавши четверту граничну умову і вважаючи, що отримаємо характеристичне рівняння, з якого визначають власні значення задачі. Після нескладних перетворень характеристичне рівняння можна подати у такому вигляді:

де - безрозмірна жорсткість пружної опори.

На рис. 3.17 а показане графічне визначення першого кореня характеристичного рівняння. Зокрема, при та отримуємо, як і слід було чекати, відомі значення та , відповідні другому і п'ятому випадкам, показаним на рис. 1.4. Результат розв’язку характеристичного рівняння наведено на рис. 3.17 б, де показано, у скільки разів критична сила в даному завданні відрізняється від критичної сили шарнірно опертого стрижня тієї самої довжини: , де

При різній безрозмірній жорсткості форми втрати стійкості виявляються якісно різними, причому при значеннях , що безперервно змінюються, якісна зміна форм втрати стійкості відбувається стрибкоподібно.

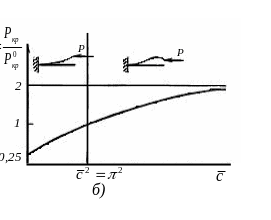
Рисунок 3.17

Задачу стійкості стрижнів на пружних основах і опорах можна розв’язати і енергетичним методом. Для цього у виразі зміни повної потенціальної енергії повинні бути враховані: енергія пружної основи і енергія деформації пружних опор. Записуючи вираз зміни повної енергії, наприклад у формі Брайана, отримаємо

де другий доданок характеризує енергію пружної основи, третій – енергію деформації пружних опор, а - число пружних опор.

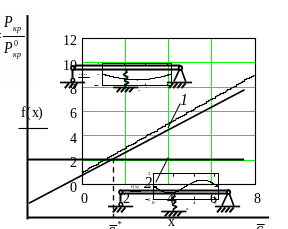
Проте енергетичний метод може дати добрий наближений розв’язок при невеликому числі членів ряду тільки тоді, коли є повністю зрозуміла якісна картина втрати стійкості. Наприклад, для шарнірно опертого стрижня з однією симетрично розміщеною проміжною пружною опорою (рис. 3.18 а) неважко уявити собі, що при малій жорсткості опори стрижень втрачає стійкість за формою 1, близькою до однієї півхвилі синусоїди. Крім того, через симетрію задачі завжди можлива втрата стійкості за формою 2, при якій пружна опора не деформується. Для форми 1 критичну силу можна отримати, задаючи прогинання стрижня у вигляді ряду

a)

б)

Рисунок 3.18

Причому, обмежившись навіть одним членом ряду, можна бути упевненим у тому, що істотної якісної помилки в значенні не буде. Дійсно, враховуючи, що для даної задачі з умови отримуємо

,

звідки

де

Для форми 2 можна записати, що

Отримані результати ілюструються графіком (рис. 3.18 б). При реалізується форма 1. Причому зі зростанням збільшується При реалізується форма 2 та незалежно від жорсткості пружної опори. Жорсткість пружної опори , при якій відбувається зміна форм втрати стійкості, знаходимо так, як це раніше було зроблено з умови . Так, обмежуючись тільки одним членом ряду, отримуємо Точне значення

При розв’язанні задачі енергетичним методом не завжди вдається отримати надійний результат. Наприклад, навіть для зовні нескладної задачі зображеного на рис. 3.20 стрижня неможливо передбачити форму втрати стійкості і, отже, важко підібрати відповідну систему апроксимуючих функцій. У цьому випадку краще використовувати метод скінчених елементів.

Рисунок 3.19