1.1 Стійкі і нестійкі стани рівноваги

Наочною ілюстрацією стійкої і нестійкої рівноваги є поведінка важкої кульки на гладкій поверхні (рис. 1.1 а). Інтуїція і досвід підказують, що поміщена на увігнуту поверхню кулька залишиться на місці, а з опуклої і сідлоподібної поверхонь вона скотиться. Положення кульки на увігнутій поверхні є стійким, а положення кульки на опуклій і сідлоподібній поверхнях - нестійким. Аналогічно два сполучених шарніром прямих стрижні під дією сили, що розтягує, знаходяться в стійкому положенні рівноваги, а при стискаючій силі – в нестійкому (рис.1.1 б).

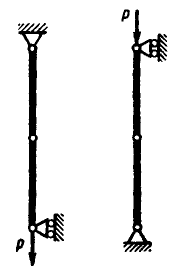
а) б)

Рисунок 1.1

Інтуїція може дати правильну відповідь тільки в простих випадках; для складніших систем однієї інтуїції недостатньо. Наприклад, навіть для порівняно простої механічної системи, зображеної на рис. 1.2 а, інтуїція може підказати лише те, що положення кульки на вершині при дуже малій жорсткості пружини буде нестійким, а зі збільшенням жорсткості пружини воно повинно стати стійким. Для системи з’єднаних шарнірами стрижнів, показаної на рис. 1.2 б, на основі інтуїції можна сказати тільки, що початкове положення рівноваги цієї системи стійке або нестійке залежно від співвідношення між силою, жорсткістю пружини і довжиною стрижнів.

Стійкість або нестійкість рівноваги пружного тіла залежить від його розмірів, матеріалу, величин та напрямку сил. Так, прямолінійний стальний стрижень при деякому значенні стискаючої сили може знаходитися у стані стійкої рівноваги, а дерев’яний стрижень таких самих розмірів при тому самому значенні сили – у стані нестійкої рівноваги.

Значення сили, навантаження і напруження, при якому вихідна форма рівноваги пружного тіла стає нестійкою, називається відповідно критичною силою, критичним навантаженням і критичним напруженням.

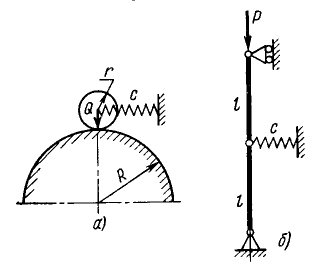
a) б)

Рисунок 1.2

Дослідження стійкості та визначення критичних сил чи навантажень має велике практичне значення, оскільки для будь-якої споруди, конструкції, системи чи їх елементів повинна забезпечуватися стійкість заданої (вихідної) форми рівноваги при дії прикладених до нього сил. Різка зміна форми якого-небудь елемента може викликати руйнування всієї конструкції.

Поняття стійкості не треба плутати з поняттям міцності. Так, наприклад, стиснутий стрижень під дією на нього навантаження, що перевищує критичне, вигнеться, але при цьому його деформації можуть бути пружними, і він після зняття навантаження відновить свою первісну форму. Тобто в цьому випадку втрата стійкості не пов’язана із втратою міцності.

Спочатку розглянемо найбільш просту і водночас одну з найважливіших інженерних задач, що пов’язані з проблемою стійкості – поздовжній вигин стрижня.

Розглянемо прямий стрижень постійного перетину з шарнірно опертими кінцями, що навантажений центрально прикладеною стискаючою силою (рис.1.3 ).

Для визначення критичної сили відхилимо стрижень і дослідимо, при якому найменшому значенні сили стрижень зможе не повернутися у попереднє положення.

Оскільки втрата стійкості стрижня виникає при малих його деформаціях, то скористаємося лінійним диференціальним рівнянням пружної лінії, яке отримане в курсі «Опір матеріалів»:

де - згинальний момент в перетині з абсцисою ; - жорсткість поперечного перетину на згин.

Рисунок 1.3

Тобто

, або

де

Розв’язок цього диференційного рівняння має вигляд

Довільні константи і визначаються з граничних умов. Для даного стрижня

.

З цих умов випливає, що

звідки

Розв’язок при не задовольняє умову задачі. Найменше значення , що не дорівнює нулю, отримуємо при :

Остання формула вперше була отримана Ейлером, тому критична сила називається також ейлеровою критичною силою.

Якщо стискаюча сила менша за критичну, то можлива тільки прямолінійна форма рівноваги, яка є стійкою.

Формулу Ейлера для визначення критичної сили при різних закріпленнях кінців стрижня можна подати в такому загальному вигляді:

або (1.1)

де - коефіцієнт зведеної довжини, що показує, у скільки разів слід збільшити довжину шарнірно опертого стрижня, щоб критична сила для нього дорівнювала критичній силі стрижня завдовжки при даних граничних умовах. Коефіцієнт показує, у скільки разів критична сила даного стрижня відрізняється від критичної сили шарнірно опертого стрижня тієї самої довжини . Значення цих коефіцієнтів наведені на рис 1.4.

При втраті стійкості викривлення стрижня відбувається, як правило, у площині, що є перпендикулярною до головної осі мінімуму поперечного перетину, тобто при вигині стрижня його перетини обертаються навколо цієї осі. Тому критичну силу слід визначати за значенням головного центрального моменту інерції . Винятки можуть бути лише у випадках, коли умови закріплення кінців стрижня в різних площинах, що проходять через його вісь, є різними.

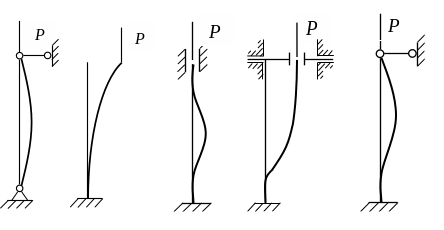
Рисунок 1.4

За значенням критичної сили можна визначити викликане нею критичне стискаюче напруження:

де , що дорівнює відношенню зведеної довжини стрижня до радіуса інерції поперечного перетину стрижня, називається гнучкістю стрижня.

Отримані результати справедливі лише тоді, коли напруження в матеріалі, що викликані критичною силою, не перевищують границі пропорційності. Це випливає з того, що в основу виведення формул покладено диференціальне рівняння пружної лінії, яким можна користуватися лиже в межах застосування закону Гука.

З умови отримуємо умову, при якій можна використовувати формулу Ейлера (1.1)

Також треба відмітити, що в більшості практичних випадків закріплення кінців стрижнів відбувається накладанням не абсолютно жорстких зв’язків, а зв’язків, що можуть деформуватися. Теоретичне дослідження стійкості таких стрижнів ускладнюється деякою невизначеністю ступеня податливості реальних зв’язків.