3.3 Розв’язання задач стійкості стрижнів енергетичним методом

Задачу стійкості прямого стрижня розглянемо з урахуванням припущень, сформульованих в п.3.1, але для її розв’язання скористаємось енергетичним підходом.

На рис. 3.8 зображений пружний стрижень, що перебуває під дією розподіленого навантаження і зосередженої сили , причому правий кінець стрижня пружно закріплений щодо поздовжніх переміщень. Параметри початкового напружено – деформованого стану такого стрижня при невикривленому стані вважаємо відомими (тут - жорсткість стрижня на розтягування, - початкове осьове переміщення).

Рисунок 3.8

Для того щоб при викривленні осі стрижня виразити зміну повної потенціальної енергії у формі Брайана, повідомимо точкам осі стрижня поперечні переміщення першого порядку малості (рис. 3.9 а).

Зміну повної потенціальної енергії стрижня при переході від прямолінійної форми рівноваги до нового викривленого стану визначимо з точністю до величин другого порядку малості (див. п. 2.2). Як і раніше, подамо у вигляді суми двох доданків: , де - потенціальна енергія вигину стрижня; - зміна потенціальної енергії розтягування стрижня, що викликана поперечним переміщенням .

а) б)

Рисунок 3.9

Оскільки згідно із прийнятим припущенням (див. п.3.1) вигин стрижня при втраті стійкості описується звичайною теорією вигину балок, можна записати (див. п.2.1)

(3.15)

Для підрахунку знайдемо подовження осі стрижня , що викликаються поперечними переміщеннями (рис. 3.9 б).

.

Скориставшись розкладанням в ряд функції і залишаючи лише квадратичні члени розкладання (оскільки зміну повної енергії досить знати з точністю до величин другого порядку малості), отримаємо

.

Оскільки є поперечні переміщення стрижня, то початкові навантаження здійснюють роботу на цих подовженнях, тобто

Таким чином,

(3.16)

Оскільки при виведенні виразу (3.16) точки осі стрижня здійснювали тільки поперечні переміщення , «мертві» поздовжні зовнішні навантаження, що не здійснюють роботу на поперечних переміщеннях, не увійшли до цього виразу.

З умови стаціонарності (або з умови при додатковій вимозі мінімуму критичного навантаження) можна знайти (точно або приблизно) точки біфуркації прямолінійної початкової форми рівноваги стрижня. Зокрема, з умови стаціонарності випливає основне лінеаризоване рівняння (3.4) і можливі для цього рівняння граничні умови. Дійсно, прирівнявши до нуля першу варіацію зміни повної потенціальної енергії , отримаємо

(3.16 а)

Послідовно проінтегруємо по частинах

Звідси випливає основне лінеаризоване рівняння (3.4) й однорідні граничні умови при та :

або

або

Енергетичний критерій у формі Брайана (3.16 а) (так само, як отримане на його основі основне лінеаризоване рівняння) справедливий за будь-яких умов закріплення стрижня в осьовому напрямі. Ці умови закріплення повинні враховуватися при визначенні початкових осьових зусиль

При виведенні виразу (3.16) були враховані тільки переміщення першого порядку малості , що переводили стрижень з початкової прямолінійної форми рівноваги в суміжну форму рівноваги із зігнутою віссю. При цьому додаткові осьові переміщення вважали такими, що тотожно дорівнюють нулю. Неважко показати, що остаточний вираз (3.16) не зміниться, якщо, окрім поперечних переміщень , врахувати додаткові осьові переміщення другого порядку малості (див. п.2.3). Ця обставина дозволяє перейти від енергетичного критерію стійкості у формі Брайана до енергетичного критерію у формі С.П. Тимошенко. Для зображеного на рис. 3.8 прямого стрижня замість загального виразу (2.63) отримаємо

(3.17)

де - потенціальна енергія вигину стрижня, що підраховується за формулою (3.15). Замість системи рівнянь (2.60) отримаємо одне рівняння

(3.18)

де - додаткове осьове зусилля.

При додаткових осьових переміщеннях, що не дорівнюють нулю, подовження дорівнюватимуть

Враховуючи, що , з (3.18) отримуємо диференціальне рівняння, що дозволяє виразити додаткові переміщення другого порядку малості через поперечні переміщення першого порядку малості:

(3.19)

У даному випадку граничними умовами, очевидно, будуть: Двічі інтегруючи (3.19) і враховуючи першу з цих граничних умов, знаходимо

(3.20)

Постійна визначається з другої граничної умови. Зокрема, при отримуємо та

(3.21)

У цьому випадку і тобто перехід від прямолінійного стану рівноваги до викривленого відбувається без додаткового розтягування осі стрижня. Тоді зміна повної потенціальної енергії стрижня

(3.22)

При , коли з виразу (3.20) отримуємо

(3.23)

(3.24)

Причому додаткові осьові подовження та зусилля не дорівнюють нулю, а визначаються виразами

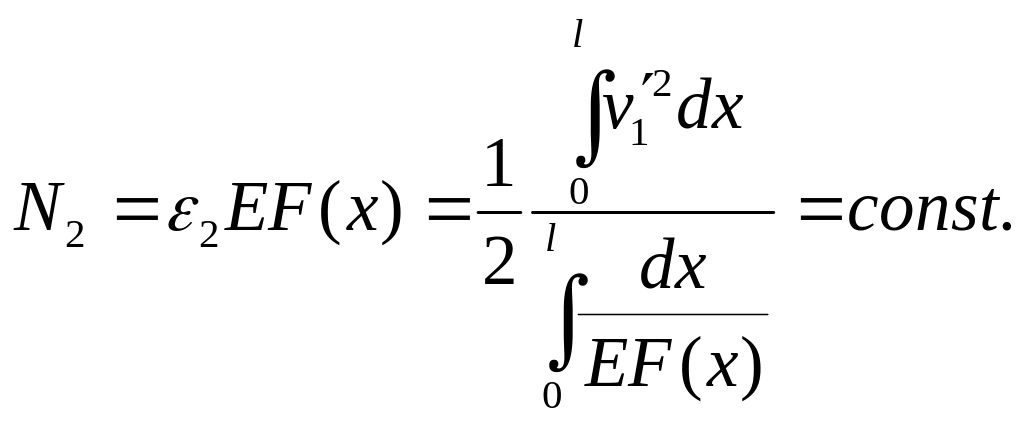
Коли зміна повної потенціальної енергії підраховується у формі С.П. Тимошенко, виражається безпосередньо через зовнішні навантаження, а початкові осьові зусилля до виразу (3.17) не входять.

Подальше розв’язання можна вести (точно або приблизно) з умови або при додатковій вимозі мінімуму навантаження. Вираз зміни повної потенціальної енергії у формі С.П. Тимошенко зручний для наближеної оцінки критичних навантажень у тих випадках, коли втрата стійкості стрижня може відбуватися без розтягування його осі, тобто коли справедлива залежність (3.22). Зокрема, з цієї залежності можна отримати добре відому з курсу опору матеріалів формулу для стискаючої критичної сили, яка була вже отримана в п.2.3

де - функція, що задовольняє геометричні граничні умови задачі і дає мінімум значенню .

Як показано в [1], більшість авторів, формулюючи енергетичний метод розрахунку на стійкість стиснутих стрижнів, вважають умову нерозтяжності осі стрижня (3.21) очевидною і користуються нею без будь-яких застережень і обмежень. Проте неважко навести приклади, коли ця умова нерозтяжності не може бути виконана або призводить до неправильного результату. Так, наприклад, стрижень із закріпленими щодо осьових зсувів кінцями (рис. 3.10, а) не може втратити стійкість без зміни довжини осі. Якщо при дослідженні стійкості середнього стрижня системи, показаної на рис. 3.10, б, вважати його вісь нерозтяжною, то це може привести до заниженого значення критичної сили.

Розглянемо розв’язання ще декількох задач стійкості стрижнів енергетичним методом. Дослідимо стійкість шарнірно опертого стрижня при двох варіантах закріплення верхнього кінця в осьовому напрямі (рис. 3.11 а і б):

1) верхній кінець може вільно зміщуватися в осьовому напрямі;

2) верхній кінець закріплений нерухомо.

1. б)

Рисунок 3.10

1. б)

Рисунок 3.11

Очевидно, і в тому і в іншому випадку розв’язок можна отримати за допомогою ряду

(3.25)

що задовольняє всі граничні умови задачі. У першому випадку наближений розв’язок зручно отримувати, подавши зміну повної потенціальної енергії у формі С.П. Тимошенко, тобто у формі (3.22), як це, як правило, робиться в курсі «Опір матеріалів». Прирівнюючи до нуля (3.16), знаходимо

Тобто при

Оскільки критичним є найменше зі знайдених значень навантаження, то з умови при , обмежуючись першим членом ряду (3.25), отримуємо (при точному розв’язку ).

Якщо у виразі для зберегти більше число членів ряду і використати умову мінімуму значення за параметрами , при довільному законі зміни згинальної жорсткості стрижня критичне навантаження можна знайти практично з будь-яким ступенем точності.

Оскільки потрібно визначити функцію тільки з точністю до масштабу, всі параметри зручно віднести до такого параметра , який не дорівнює нулю, і вести пошук мінімуму за безрозмірними параметрами , де

У другому випадку (рис. 3.11 б) при нерухомо закріпленому верхньому кінці стрижня, як відмічено, втрата стійкості без розтягнення осі стрижня неможлива. Тому при розв’язанні у формі С.П. Тимошенко не можна визначати осьові переміщення другого порядку малості за залежністю (3.21). Для визначення цих переміщень необхідно використовувати громіздкіший вираз (3.23). Методично в таких випадках, мабуть, більш виправдано проводити розвязання у формі Брайана, побудувавши заздалегідь залежність . Тоді згідно із залежністю (3.16) можна записати

де - коефіцієнт, що залежить від відношення і закону зміни жорсткості стрижня на розтягуванні Прирівнюючи до нуля, знаходимо

Подальше розв’язання проводимо за описаною схемою: вводимо безрозмірні параметри та, мінімізуючи вираз для при деякому вибраному числі варійованих параметрів, знаходимо .

Слід зазначити особливість даної задачі: ця задача не є позитивно визначеною. При розв’язанні подібних задач наближені методи слід застосовувати з обережністю. Якщо в задачі обмежитися одним членом ряду (3.25), то похибка наближеного розв’язку може виявитися скільки завгодно великою. Так, наприклад, для та , взявши отримаємо безглуздий результат . Тому розв’язання слід починати, принаймні, з двох членів ряду. Зокрема, при , , отримаємо

Умова екстремуму зовнішнього навантаження приводить до значення масштабного коефіцієнта Отже, наближене значення критичного навантаження дорівнює

а форма зігнутої осі описується функцією

В отриманих формулах знаки « »означають, що до втрати стійкості приводять сили, спрямовані як вниз, так і вгору. Через симетрію задачі абсолютні значення додатного і від’ємного критичних навантажень збігаються. У загальному випадку за відсутності симетрії задачі отримують два критичні значення навантажень, різних за абсолютною величиною. Точне значення критичної сили для даної задачі становить . Тобто різниця не перевищує 20%, що цілком задовольняє інженерну точність розрахунку.

Наближений розв’язок задачі енергетичним методом практично не ускладнюється у разі, коли на стрижень діють не лише зосереджені, а й розподілені поздовжні навантаження типу власної ваги (рис. 3.12). Причому якщо втрата стійкості можлива без розтягування осі стрижня, то зручніше використовувати критерій стійкості у формі С.П. Тимошенко, інакше – у формі Брайана.

Рисунок 3.12

Так, наприклад, для зображеного на рис. 3.12 а стрижня критичне значення розподіленого навантаження може бути знайдене зі співвідношення, що випливає з умови та виразу (3.22):

де знак «-» узятий відповідно до напряму діючого навантаження. При постійних та , взявши у вигляді першого члена ряду (3.25), з цього співвідношення отримуємо

,

з урахуванням того, що , остаточно можемо записати

.

Звідси найменше, а отже, критичне значення дорівнює

Точне значення для цієї задачі Тобто розв’язок, отриманий з урахуванням лише одного члена ряду, відрізняється від точного лише на 6,5%.

Для стрижня, наведеного рис. 3.12 б, критичне значення навантаження, мабуть, зручніше визначати, використовуючи вираз (3.16)

У випадку стрижня з постійною жорсткістю на розтягування і при постійному розподіленому навантаженні , зокрема, матимемо

Обмежившись двома першими членами ряду (3.25) (якщо залишити тільки один член ряду, то знову отримаємо абсурдний результат ), отримаємо (читачам пропонується самим переконатися в отриманому результаті):

Для п'яти членів ряду критичне значення дорівнює

.

При подальшому збільшенні числа членів ряду це значення не змінюється, тому можна вважати його точним.

Для стрижнів при навантаженнях, що змінюються за довільним законом , змінній жорсткості і будь-яких інших граничних умовах при розв’язанні задачі стійкості використовується той самий порядок, що наведений вище.

Треба зазначити, що в тих випадках, коли «мертві» зовнішні навантаження передаються на стрижень за допомогою деяких механізмів, до виразів зміни повної потенціальної енергії (3.16) і (3.17) увійдуть, природно, додаткові доданки. Наприклад, якщо «мертва» сила передається на стрижень за допомогою жорсткого важеля довжиною (див. рис. 3.3 а), то при вигині стрижня потенціал цієї сили додатково зміниться на величину - , де Аналогічно можна підрахувати додаткові доданки і при інших схемах передачі зовнішніх сил на стрижень.